concoide

Enciclopedia on line

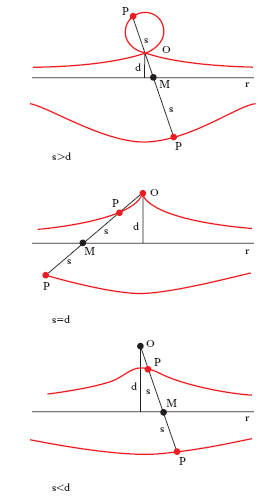
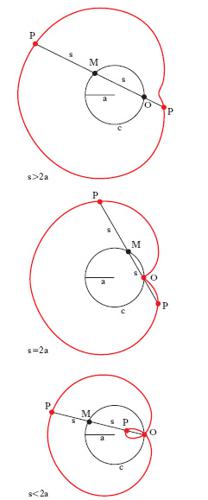
concoide In matematica, la c. di una data curva c, rispetto a un punto O, è così definita: su una retta uscente da O, a partire dalle intersezioni M con la c, si riporta (da una parte e dall’altra) un segmento MP (intervallo) di lunghezza s prefissata; c. della curva C è il luogo dei punti P al variare della retta per O. La c. della retta (o c. di Nicomede; fig. 1) risulta essere la curva del 4° ordine di equazione (x−d)2 (x 2 +y 2 )− s 2 x 2 =0 (d è la distanza di O dalla retta r; assi x e y sono la perpendicolare e la parallela a r per O). La c. della circonferenza (rispetto a un punto O su di essa; fig. 2) è la lumaca di Pascal che assume, per la sua forma, il nome di cardioide quando, in particolare, s=2a (a è il raggio del cerchio). Prendendo come assi x e y il diametro per O e la tangente al cerchio in O, l’equazione della lumaca di Pascal è:

(x 2 + y 2 − 2 a x)2 − s 2 (x 2 + y 2 ) = 0.

Vedi anche
cardioide Curva algebrica piana ottenuta a partire da una circonferenza di raggio a (v. fig.) e dal fascio di rette passanti per un suo punto O, staccando su ciascuna retta segmenti 2a da ambo le parti delle ulteriori intersezioni con la circonferenza stessa: (x2 + y2)2 − 4ax (x2 + y2) − 4a2y2 = 0. La cardioide ... intersezione matematica Nella geometria elementare, l’insieme dei punti comuni a due o più insiemi dati, sinonimo di interferenza. In geometria algebrica tale insieme si chiama interferenza, mentre si riserva il nome di intersezione al medesimo insieme quando i suoi punti siano considerati con la loro molteplicità ... diametro matematica In una circonferenza o un cerchio, la lunghezza di un segmento, o il segmento stesso, che partendo da un punto della circonferenza passa per il centro e termina nel punto opposto della stessa; la lunghezza del diametro d e della circonferenza c sono legate dalla relazione c=πd, dove π è il ... ordinata matematica Una delle coordinate cartesiane di un punto del piano o dello spazio, ed esattamente quella che si usa scrivere per seconda; le altre due sono l’ascissa (la prima) e la quota (la terza, nello spazio). Con riferimento al piano, dati due assi cartesiani ortogonali x e y (v. fig.), l’ordinata ...
Categorie
Tag
Vocabolario
concòide
concòide agg. e s. f. [dal gr. κογχοειδής «a forma di conchiglia, curvo come la superficie di una conchiglia», comp. di κόγχη «conchiglia» e -ειδής «-oide»]. – 1. agg. In mineralogia, frattura concoide, frattura a superficie curva. 2. s. f. In matematica,...
argoviano
argoviano agg. e s. m. (f. -a). – 1. Dell’Argovia, cantone della Svizzera; come sost., abitante, nativo, originario dell’Argovia. 2. s. m. Sottopiano geologico del Malm rappresentato da marne e calcari marnosi a frattura concoide, rinvenuti nel territorio...
0