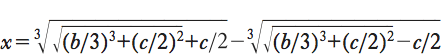Cardano, Girolamo

Girolamo Cardano

Autore fra i più letti in Europa nel corso dei secoli 16° e 17°, Girolamo Cardano scrisse numerosissime opere di matematica, medicina, astrologia, filosofia. La sua opera matematica è universalmente riconosciuta come uno dei contributi fondamentali nel campo delle ricerche algebriche. La sua riflessione sul moto e le macchine costituisce una problematica concettuale importante per il futuro sviluppo della scienza.

La vita

Girolamo Cardano (o Gerolamo) nacque a Pavia il 24 settembre 1501 dal giureconsulto Fazio Cardano e da Chiara Micheri, genitori non sposati. Di salute cagionevole, fu educato in maniera piuttosto irregolare dal padre, e solo dopo avere compiuto i diciannove anni si trasferì da Milano a Pavia per frequentare la facoltà di Arti e Medicina. All’inizio del 1524, si iscrisse all’Università di Padova e, in quello stesso anno, si laureò in artibus a Venezia. Nel 1526 seguì la laurea in medicina a Padova. Da quell’anno al febbraio 1532 praticò l’attività medica in Saccolongo (presso Padova), dove sposò Lucia Bandarini.

Dopo un primo tentativo di aggregazione al Collegio dei physici (medici) di Milano (1529), nel 1532 decise di rientrare a Milano, ma a seguito di un nuovo rifiuto da parte del Collegio andò ad abitare a Gallarate, rimanendovi diciannove mesi. Da questo periodo di grande difficoltà cominciò a risollevarsi nel momento in cui ebbe la possibilità, sul finire del 1534, di insegnare aritmetica e geometria presso le scuole Piattine, fondate a Milano nel 1501 da Tommaso Piatti.

Intanto aveva pubblicato alcune brevi opere, di carattere astrologico e di argomento medico; fu però solo con la pubblicazione della Practica arithmetice & mensurandi singularis (1539), nello stesso anno della sua definitiva aggregazione al Collegio dei physici, che raggiunse la fama europea; questa gli permetterà tra l’altro di stampare le sue opere a Norimberga e a Basilea.

Più volte professore di medicina teorica nella facoltà medica pavese tra il 1546 e il 1562, pubblicò in quegli anni alcune delle sue opere più importanti: Artis magnae sive de regulis algebraicis liber unus, meglio nota come Ars magna (1545), De subtilitate (1550), vera summa del suo pensiero filosofico-scientifico (ampliata e ripubblicata nel 1554 e nel 1560), De rerum varietate (1557), nella quale integrò e rielaborò molte questioni toccate nell’opera precedente.

L’arresto nel 1560 del prediletto figlio Giovanni Battista (accusato di uxoricidio) e la sua successiva condanna a morte sconvolsero irrimediabilmente la vita di Cardano che, nel 1570, subì addirittura un’incarcerazione da parte del tribunale dell’Inquisizione di Bologna, città in cui si era trasferito dal 1562. Con questa vicenda terminò la sua carriera universitaria. Nello stesso anno del suo arresto uscì a Basilea l’Opus novum de proportionibus. Cardano trascorse gli ultimi anni di vita a Roma. Vi morì il 21 settembre 1576, lasciando numerosissime opere manoscritte (tra cui i Paralipomena), che vedranno la luce solo negli Opera omnia in 10 volumi, editi a Lione nel 1663.

L’opera matematica

Il fondamentale contributo dato da Cardano alla scoperta della formula generale per la soluzione delle equazioni di terzo grado ha da sempre dominato l’interesse degli storici della matematica. Questo dato di fatto ha incontestabili ragioni d’essere, che giustificano il rilievo dato a questo particolare aspetto della sua opera, ma che però non legittimano la rinuncia a una lettura generale e trasversale dei testi matematici di Cardano, certamente non altrettanto innovativi, ma comunque profondamente ancorati alle pratiche di studio e insegnamento della sua epoca.

Cardano aveva appreso dal padre i primi rudimenti dell’aritmetica, e aveva iniziato con l’aiuto del genitore lo studio dei primi sei libri degli Elementi di Euclide. Non è quindi sorprendente che anche i suoi primi tentativi scientifici riguardassero argomenti legati alla matematica, come, per es., il calcolo della distanza fra due città, o fra due stelle di longitudine e latitudine conosciuta. Questioni di carattere elementare, ma alle quali presto, per lo meno dagli anni 1524-25, dovettero affiancarsi indagini più complesse e originali, come quelle relative alla teoria dei giochi, sviluppata all’interno di un testo intitolato De ludis. Del materiale in esso raccolto è rimasta solo la parte relativa al gioco dei dadi, pubblicata postuma, con il titolo Liber de ludo aleae, negli Opera omnia.

Cardano amò moltissimo il gioco d’azzardo, tanto che nella sua autobiografia confessò di aver giocato a dadi quasi ogni giorno per circa venticinque anni. Il Liber de ludo aleae è dunque il frutto di questa passione e, sebbene sia solitamente citato soprattutto in rapporto allo sviluppo del calcolo delle probabilità, non dovrà essere letto solo in riferimento al sorgere dei primi tentativi di teorizzazione matematica dei giochi d’azzardo. Questo libro contiene infatti anche riflessioni morali, storiche e tecniche sul gioco dei dadi. È dunque in tale contesto che le riflessioni di Cardano, relative alla determinazione del rapporto tra casi favorevoli e risultati possibili in lanci con 1, 2, o 3 dadi, vanno analizzate.

Ed è forse proprio in riferimento alla pratica reale del gioco che si può spiegare il metodo di calcolo basato sulla aequalitas, fondato sulla divisione per 2 dei risultati possibili che, come lo stesso Cardano riconosce, può portare a numeri assai diversi rispetto a quelli ottenuti tramite l’attenta analisi delle singole combinazioni realizzabili. Osservato da un diverso punto di vista, questo metodo può quindi apparire non tanto come il frutto di un’errata soluzione del problema proposto, quanto piuttosto come un primo grezzo tentativo di offrire al giocatore una semplice regola per la quantificazione del valore atteso, elemento essenziale per determinare la congruenza tra la probabilità di ottenere un determinato risultato e l’eventuale vincita (Williams 2005, pp. 30-31).

Argomenti maggiormente legati alla tradizione delle scuole d’abaco caratterizzano invece la Practica arithmetice. Il testo presenta un’agile trattazione di tutto quanto concerne la numerazione, le operazioni (comprese estrazioni di radici e progressioni) e le soluzioni dei problemi legati alla monetazione, al calcolo di interessi e alla pratica dei commerci. Accanto a questa esposizione, tipica della manualistica del tempo, Cardano inserisce anche questioni in parte eccentriche rispetto alla matematica mercantile. I casi del problema archimedeo della corona di Gerone, descritto nel De architectura (seconda metà del 1° sec. a.C.) di Marco Vitruvio Pollione, o quello del calcolo del grado di frigiditas o caliditas di un farmaco composto, affrontato con diverse modalità all’interno della tradizione medica, sono emblematici a questo riguardo. Soffermandoci solo sulla questione archimedea, Cardano individua una procedura algebrica per determinare le percentuali di oro e argento presenti in un oggetto, che risulta valida non solo nel caso in cui la corona e le due masse di oro e argento siano ugualmente pesanti, ma anche quando questi tre dati del problema assumano valori diversi e a piacere (Gavagna, in Girolamo Cardano: le opere, le fonti, la vita, 1999, pp. 300-301).

Per quanto riguarda le ricerche propriamente algebriche, nella Practica non si trova ancora alcuna traccia della formula risolutiva generale delle equazioni di terzo grado. D’altra parte il 1539, data di uscita dell’opera, fu proprio l’anno in cui Cardano ottenne dal matematico bresciano Niccolò Tartaglia il metodo per la soluzione delle equazioni del tipo x3+bx=c, o, come si diceva allora, del «capitolo di cubo e cose uguale a numero».

Ciononostante, sono proprio alcuni dei risultati presenti all’interno di questo testo che ci fanno comprendere a pieno il livello di padronanza della tecnica algebrica posseduta da Cardano, che gli permise in seguito di generalizzare e superare il metodo suggeritogli da Tartaglia. Artifici per abbassare di un grado equazioni del tipo x3=bx+c (capitolo di cubo uguale a cose e numero), o del tipo x3+c=bx (capitolo di cubo e numero uguale a cose), oppure tentativi non riusciti di risoluzione, sono soltanto alcuni dei risultati acquisiti. Essi sono i prodromi di quella capacità operativa che permetterà successivamente a Cardano di ritrovare le trasformazioni necessarie per far scomparire il termine di secondo grado nelle equazioni cubiche.

Nella parte algebrica della Practica, Cardano persegue ciò che era già stato invano cercato dai matematici delle generazioni precedenti, cioè l’individuazione di regole generali che permettessero di risolvere un folto gruppo di equazioni (non riconducibili allora a un’unica forma a causa dell’esclusione dei numeri negativi e dello zero dal novero degli oggetti matematici). Ma Cardano non riuscì nell’impresa, e si venne a trovare nelle stesse condizioni dei suoi predecessori, cosicché egli avrebbe potuto a sua volta sottoscrivere le parole di Luca Pacioli e ammettere che

de numero cosa e cubo fra loro siando composti [x³=bx+c, x³+bx=c, x³+c=bx], over de numero censo e cubo [x³=bx²+c, x³+bx²=c, x³+c=bx³], over de numero cubo e censo de censo [x⁴=bx³+c, x⁴+bx³=c, x⁴+c=bx³], non se possuto finora troppo bene formare regole generali (L. Pacioli, Summa de arithmetica, geometria, proportioni et proportionalita, 1494, f. 150r).

Eppure, come detto, in quello stesso 1539 Cardano aveva ottenuto da Tartaglia, con solenne promessa di segretezza, la formula risolutiva dell’equazione x³+bx=c, prima attraverso un componimento poetico piuttosto enigmatico, e poi con una sua applicazione a un esempio concreto: x³+3x=10. Si trattava di prendere due numeri U e V in modo tale che la loro differenza fosse uguale al numero (U–V=c) e che il loro prodotto fosse, come scriverà in seguito Tartaglia, «a ponto 1, cioè el cubo della terza parte delle cose [UV=(b/3) ³]» (Quesiti et inventioni diverse, 1546, f. 124r-v). Trovate le due dette quantità, sarebbe stato poi necessario prendere il loro «lato cubo», e infine sottrarre la quantità minore dalla maggiore. Partito da questo esempio, Cardano riuscì in seguito non solo a risolvere le altre due equazioni x³=bx+c, x³+c=bx, già inserite nello stesso componimento poetico inviatogli da Tartaglia, ma anche un gran numero di altre equazioni aventi il termine di secondo grado, che veniva poi fatto scomparire tramite opportune procedure.

Forte di questi nuovi risultati, e avendo scoperto tramite Annibale della Nave nel 1542 un fatto tenuto fino allora segreto, cioè che la soluzione dell’equazione x³+bx=c era stata trovata già a inizio secolo da Scipione Dal Ferro (1465-1526), Cardano pubblicò i frutti delle sue ricerche nell’Ars magna, rendendo comunque espressamente conto del contributo ricevuto da Tartaglia. Tramite questo testo, veniva così divulgata per la prima volta una formula generale per la soluzione delle equazioni di terzo grado, che in termini moderni possiamo così esprimere:

Questo modo di procedere fu però considerato da Tartaglia come un venir meno al giuramento. Da qui la sua reazione furiosa, che lo spinse prima a pubblicare nei Quesiti et inventioni diverse tutta la documentazione in suo possesso, per cercare di mettere nella giusta luce la natura dei rapporti intercorsi tra lui e Cardano, e successivamente a entrare in una feroce polemica con Ludovico Ferrari, allievo di Cardano e scopritore del metodo per risolvere le equazioni di quarto grado. Questa polemica sfociò in una pubblica disputa avvenuta a Milano nell’agosto del 1548 e raccolta nei famosi dodici «cartelli di matematica disfida», brevi opuscoli nei quali i due matematici si confrontano su moltissimi temi geometrici e aritmetici, includendo naturalmente anche le questioni legate alle equazioni.

Sebbene la nuova trattazione delle equazioni esposta nell’Ars magna mostrasse tutta la sua validità nei confronti di «capitoli» precedentemente ritenuti non risolvibili con regola generale, rimanevano comunque alcuni problemi irrisolti, che limitavano la portata della formula ritrovata. Il più importante era rappresentato dal cosiddetto caso irriducibile, che si verificava applicando la formula generale a equazioni del tipo x³=bx+c (cubo uguale a cose e numero). Qui, con il cambiamento di segno del termine di primo grado si potevano ottenere nel calcolo radici quadrate di numeri negativi, incomprensibili per i matematici di allora.

Chiamate sofistiche da Cardano, che le aveva incontrate anche studiando equazioni di secondo grado, queste grandezze risultavano essere enti matematici sconosciuti (saranno successivamente chiamati numeri immaginari), e difficilmente gestibili all’interno delle consuete procedure di calcolo. Diversamente da quanto succedeva nelle equazioni di secondo grado, in cui la presenza di tali «quantità sofistiche» implicava la mancanza di soluzioni, in quelle di terzo grado, come, per es., nel caso irriducibile, si perveniva infatti all’individuazione di più radici reali. Il problema di come ci si sarebbe dovuti comportare in presenza di queste strane grandezze occupò Cardano per tutto il resto della vita.

Il frutto delle sue ricerche in questo campo è raccolto nel De aliza regula liber (1570). In questo lavoro, Cardano cercò in primo luogo di trasformare i termini dell’equazione con opportune sostituzioni, per poi eguagliare i due membri della stessa. Riuscì così a evitare le radici di numeri negativi, ma a patto sempre di soddisfare determinate condizioni, che derivano dall’assunzione dell’incognita come lato di un corpo solido geometrico. Di fronte a tali limitazioni, Cardano cercò altre vie e, allontanandosi dalle modalità usuali di interpretazione geometrica del problema, intravide nella dottrina delle sezioni coniche la possibilità di trovare il segmento corrispondente alla quantità ricercata su nuove basi (Maracchia 2003, pp. 151-54).

Tutto questo avveniva negli stessi anni in cui il bolognese Raffaele Bombelli trovava una dimostrazione geometrica «in superficie piana» dell’esistenza di radici reali per l’equazione x³=6x+4. Con tale prova, i numeri immaginari entravano a pieno diritto nella matematica, e con le procedure di calcolo messe a punto dallo stesso Bombelli iniziava lo studio di quelli che sarebbero stati definiti numeri complessi. Era una nuova fase della ricerca algebrica, a cui Cardano, morto nel 1576, non avrebbe partecipato.

Le ‘macchine’ e l’indagine dei moti presenti in natura

Sebbene Cardano evidenzi come maggiore novità della propria filosofia naturale la dottrina degli elementi esposta nel secondo libro del De subtilitate (riduzione a tre del loro numero, con l’esclusione del fuoco, e individuazione di due sole qualità primarie: caldo e umido), ciò che invece colpisce il lettore moderno della sua opera è l’ampio spazio dato nel primo libro alla descrizione di numerose macchine (pompe idrauliche, sistemi di trasmissione del movimento, bilance ecc.).

Certo, in questo caso non si vede ancora l’elevazione della macchina a modello teorico per la spiegazione dei fenomeni naturali, assunto che caratterizzò dagli inizi del 17° sec. il meccanicismo, ma è comunque innegabile che nei testi di Cardano si concretizzi un approccio innovativo che lo condusse a una definizione più articolata di alcuni concetti chiave della filosofia naturale. Pur rimanendo all’interno di un sistema di pensiero prevalentemente aristotelico, questo ampliamento dell’oggetto d’indagine permise a Cardano di spostare l’attenzione dalle trasformazioni reciproche degli elementi e dei misti alle azioni e resistenze che gli stessi elementi e, più in generale, i corpi possono esercitare gli uni sugli altri. In precedenza, infatti, ci si era soffermati sulla questione del cambiamento di forma da parte di una certa quantità di materia, cambiamento che presupponeva l’occupazione di luoghi aventi dimensioni diverse, maggiore nel caso di un mutamento dal denso al raro e minore nel passaggio inverso. In secondo piano erano rimaste le considerazioni sulle variazioni di estensione dei corpi che mantenevano la medesima forma.

In quest’ottica, una notevole importanza rivestì lo studio delle cause del moto ascensionale dell’acqua in alcune macchine e strumenti idraulici (pompe e sifoni), solitamente spiegato in termini di horror vacui. Si trattava di una soluzione inaccettabile per Cardano, essendo il vuoto, principio difficilmente separabile dall’idea del non-essere, non necessario alla spiegazione del suddetto moto, che poteva invece essere ottenuta sulla base dei concetti di materia e di forma. Quanto avveniva, sia nei cilindri delle pompe sia nella canna del sifone, non era una reazione della natura al possibile costituirsi del vuoto, ma una diretta conseguenza della massima deformazione elastica raggiungibile dall’aria che, non potendo trasformarsi in altra sostanza, costringeva l’acqua a essa contigua a muoversi verso l’alto. Si verificavano in questo caso un sovvertimento della direzione del moto naturale dei corpi gravi e la sua subordinazione a un principio superiore, che, in un universo pieno, determinava di fatto movimenti opposti a quelli che si osservavano abitualmente.

Cardano pervenne così alla determinazione di un vero e proprio principio esplicativo dei mutamenti naturali, che potremmo definire della conservazione della forma. Quanto avveniva all’interno di apparati costruiti dall’uomo diventava così essenziale per analizzare le diverse modalità di movimento, e portava un elemento di novità rilevante all’interno della fondamentale distinzione aristotelica tra moto violento e naturale. Ciò che causava direttamente il moto ascensionale dell’acqua non era un moto violento, dato che dipendeva da un principio avente un grado di universalità ancora maggiore di quello che regolava i movimenti ‘da’ e ‘verso’ il centro del mondo. Certo il motore ultimo, cioè quello che portava l’aria alla sua massima rarefazione possibile, era di natura violenta, ma l’aria poi, agendo direttamente sull’acqua, operava secondo natura.

Su tali basi, lo studio dei moti naturali poteva servirsi dell’analisi del funzionamento di molti altri meccanismi. Questo nuovo modo di studiare il movimento partendo da una riflessione sulle diverse tipologie di macchina ebbe come conseguenza l’abbandono della partizione disciplinare presente nella meccanica antica. Questa si fondava sostanzialmente sulla diversa natura dei motori, aria o aria riscaldata dal fuoco per le macchine pneumatiche, contrappesi legati a corde per i cosiddetti automi, acqua fatta defluire in maniera regolare e costante per gli orologi ad acqua. Nella sua trattazione, Cardano di fatto non mostra l’esigenza di ridurre i vari movimenti individuati a un principio unitario che possa spiegare ogni moto. Egli si accontenta di mostrare le varie combinazioni di moto e quiete osservabili in macchine più o meno complesse. Gli elementi di novità dell’approccio non riuscirono tuttavia a concretizzarsi in un insieme di principi limitati e rigorosi. Affrontando in questo modo la questione del moto, Cardano si trovò su posizioni ancora lontane da quelle che avrebbero portato gli scienziati del 17° sec. alla fondazione della nuova scienza meccanica.

Opere

Practica arithmetice & mensurandi singularis […], Mediolani 1539.

Artis magnae sive de regulis algebraicis liber unus […], Norimbergae 1545; ed. bilingue latino-italiano Artis magnae sive de regulis algebraicis liber unus, a cura di M. Tamborini, Milano 2011.

De rerum varietate libri XVII, Basileae 1557.

De subtilitate libri XXI, Basileae 1560; ed. critica a cura di E. Nenci, t. 1, Libri I-VII, Milano 2004.

Opus novum de proportionibus numerorum, motuum, ponderum, sonorum, aliarumque rerum mensurandarum […], Basileae 1570.

Opera omnia, 4° vol., Quo continentur artithmetica, geometrica, musica, e 10° vol., Quo continentur opuscula miscellanea (in partic. Artis arithmeticae tractatus de integris, pp. 117-28; Paralipomena, pp. 510-19), cura C. Sponii, Lugduni 1663.

De libris propriis: the editions of 1544, 1550, 1557, 1562 with supplementary material, ed. I. Maclean, Milano 2004.

Liber de ludo aleae, a cura di M. Tamborini, Milano 2006.

Bibliografia

P. Cossali, Origine, trasporto in Italia, primi progressi in essa dell’algebra, 2° vol., Parma 1799, pp. 441-84.

Ø. Ore, Cardano: the gambling scholar, Cambridge (Mass.) 1953.

G. Gliozzi, Cardano Gerolamo, in Dizionario biografico degli Italiani, Istituto della Enciclopedia Italiana, 19° vol., Roma 1976, ad vocem.

Girolamo Cardano. Philosoph, Naturforscher, Arzt, hrsg. E. Kessler, Wiesbaden 1994.

N.G. Siraisi, The clock and the mirror: Girolamo Cardano and Renaissance medicine, Princeton (N.J.) 1997.

A. Grafton, Cardano’s cosmos: the worlds and works of a Renaissance astrologer, Cambridge (Mass.) 1999 (trad. it. Roma 2002).

M. Tamborini, De cubo et rebus aequalibus numero: la genesi del metodo analitico nella teoria delle equazioni cubiche di Girolamo Cardano, Milano 1999.

Girolamo Cardano: le opere, le fonti, la vita, Atti del Convegno internazionale di studi, Milano (11-13 dicembre 1997), a cura di M. Baldi, G. Canziani, Milano 1999 (in partic. M. Tamborini, Matematica, tempo e previsione nel “Liber de ludo aleae”, pp. 227-71; V. Gavagna, Alcune osservazioni sulla “Practica arithmetice” di Cardano e la tradizione abachistica quattrocentesca, pp. 273-312).

I. Schütze, Die Naturphilosophie in Girolamo Cardanos “De subtilitate”, München 2000.

S. Maracchia, Algebra e geometria in Cardano, in Cardano e la tradizione dei saperi, Atti del Convegno internazionale di studi, Milano (23-25 maggio 2002), a cura di M. Baldi, G. Canziani, Milano 2003, pp. 145-55.

D. Bellhouse, Decoding Cardano’s “Liber de ludo aleae”, «Historia mathematica», 2005, 2, pp. 180-202.

L. Williams, Cardano and the gambler’s habitus, «Studies in history and philosophy of science», 2005, 1, pp. 23-41.

V. Gavagna, Medieval heritage and new perspectives in Cardano’s “Practica arithmetice”, «Bollettino di storia delle scienze matematiche», 2010, 1, pp. 61-80.