Gli insiemi numerici

Gli insiemi numerici

Gli insiemi numerici

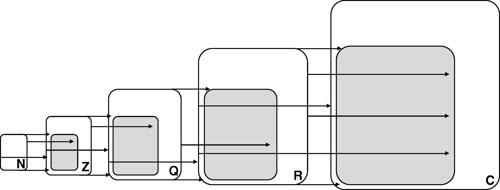
Gli insiemi numerici più importanti sono quelli dei numeri naturali, dei numeri interi, dei numeri razionali, dei numeri reali, dei numeri complessi.

￭ I numeri naturali. L’insieme dei numeri naturali viene indicato con la lettera N; in letteratura, a volte non comprende lo zero e dunque N = {1, 2, 3, ...}, a volte lo comprende e dunque, come convenuto in quest’opera, N = {0, 1, 2, 3, ...}. Come dice lo stesso aggettivo “naturale”, i numeri naturali sono numeri la cui considerazione si è presentata spontanea nella storia dell’uomo, introdotta dalla semplice esigenza di contare gli oggetti. Ugualmente, una certa astrazione è presente anche nei numeri naturali. Scriveva Cartesio: «Il numero non sta in alcun oggetto creato, ma è semplicemente un modo astratto di pensare. Quando vediamo due alberi o due uccelli e non pensiamo alla loro natura, ma solo al fatto che sono due, ci formiamo l’idea di quel numero che chiamiamo due». In alcune presentazioni, come si è detto, tra i numeri naturali viene incluso anche lo zero. Effettivamente si ottiene così una maggiore comodità in funzione degli sviluppi successivi, ma ci si allontana da un percorso storico che ha visto i numeri naturali nascere insieme con le prime forme espressive dell’uomo, mentre lo zero non compare sovente nelle popolazioni del mondo antico. Lo stesso termine zero fa la sua comparsa per la prima volta alla fine del secolo xv (come derivazione dall’arabo) e la sua necessità come cifra si impone assieme all’affermazione della notazione posizionale.

Per evitare confusione, seguendo la convenzione qui adottata, si può indicare con N l’insieme dei numeri naturali compreso lo zero e con N₀ l’insieme dei numeri naturali privato dello zero di cui, quindi, il cui primo elemento è 1. Va comunque rilevato che tali simbolismi variano a seconda degli autori e perciò occorre accertarsi del significato effettivo che assume il simbolo N oppure N₀ in una singola pubblicazione. Nell’ambito della teoria degli insiemi è possibile abbandonare una presentazione di N esclusivamente intuitiva in favore di un approccio formalmente più rigoroso. Una teoria assiomatica dei numeri naturali è stata elaborata alla fine dell’Ottocento dal matematico italiano G. Peano, che si è avvalso di tre concetti primitivi (quelli di numero, di zero e di successore) e di cinque assiomi (si veda → Peano, assiomi di).

Si possono sempre calcolare la somma e il prodotto di due numeri naturali. Non si può invece calcolare sempre la loro differenza, nel senso che non sempre il risultato della sottrazione è ancora un elemento di N: in N, a − b è possibile, nel senso che appartiene ancora a N, quando a è maggiore di b o uguale a b. Si costruisce allora un secondo insieme con l’obiettivo che contenga N (sia cioè una sua estensione), renda sempre possibile l’operazione che in N suscitava alcuni problemi (la sottrazione) e verifichi il principio di permanenza delle proprietà formali, per cui nel nuovo insieme devono continuare a valere il più possibile le proprietà che valevano nell’insieme di partenza.

￭ I numeri interi. Si arriva così a Z, l’insieme dei numeri interi relativi: Z = {0, + 1, −1, + 2, −2, ...}. A questo insieme ci si riferisce spesso indicandolo semplicemente come insieme dei numeri interi, sottintendendo l’aggettivo relativi. I numeri interi possono essere facilmente rappresentati su una retta orientata, dopo aver scelto un’origine e un’unità di misura: i numeri positivi sono collocati a destra dell’origine, quelli negativi alla sua sinistra. Ugualmente, anche il calcolo con i numeri relativi è interpretabile semplicemente ricorrendo per esempio alle temperature (sopra o sotto lo zero termico della scala prescelta) o alle altitudini, ponendo il livello del mare come quota zero. L’insieme Z ha (a differenza di N) la struttura di gruppo: è cioè un insieme chiuso rispetto a una operazione binaria (l’addizione) che soddisfa la proprietà associativa, l’esistenza di un elemento neutro (zero) e dell’inverso additivo di ogni suo elemento (l’opposto dell’elemento considerato); inoltre l’addizione soddisfa la proprietà commutativa e quindi Z(+) è un gruppo commutativo. Per Z si può fare la stessa osservazione critica avanzata per N: è sempre possibile calcolare in Z la somma, la differenza e il prodotto di due suoi elementi, ma non è sempre possibile calcolare il rapporto tra due interi relativi in quanto il risultato dell’operazione a /b, con a e b elementi di Z, non sempre è un elemento di Z. È di nuovo un’insufficienza algebrica, dunque, quella che motiva l’ulteriore estensione degli insiemi numerici (storicamente questa insufficienza è stata avvertita nell’ambito della teoria dei rapporti tra due grandezze). Si arriva così a introdurre le frazioni e a definire l’insieme Q dei numeri razionali.

￭ I numeri razionali. Sembra che la linea che compare nella scrittura delle frazioni e, quindi, dei numeri razionali espressi in tal modo, sia apparsa per la prima volta in un autore arabo del xii secolo. Nella scrittura dei numeri razionali come frazioni va esclusa la possibilità che il denominatore sia nullo; rimane quindi esclusa la divisione per zero. In effetti non la si può ottenere (neppure con un ulteriore ampliamento) senza incorrere in una contraddizione. Supponiamo infatti che ci sia un nuovo elemento x = 1/0. Avremmo allora 0 ⋅ x = 1. Supponendo ora che continui a valere il principio di permanenza delle proprietà formali, e in particolare la proprietà distributiva del prodotto rispetto alla somma, otterremmo l’assurdo 1 = 0 ⋅ x = (0 + 0) ⋅ x = 0 ⋅ x + 0 ⋅ x = 1 + 1 = 2. La struttura algebrica di Q è più ricca di quella di Z. Si dice che Q è un campo per indicare che Q è un gruppo rispetto all’addizione, che Q{0} è un gruppo anche rispetto alla moltiplicazione e che vale la proprietà distributiva della moltiplicazione rispetto all’addizione. La considerazione di Q rende ora l’insieme numerico più flessibile e idoneo a rappresentare e misurare la complessità del mondo reale. Da questo punto di vista, gli insiemi N e Z risultavano ancora abbastanza rigidi: tra due numeri interi poteva non esserci alcun altro numero intero (così capitava per due numeri consecutivi) e pertanto non era possibile raffinare una misurazione approssimata, per difetto o per eccesso. Si dice, a questo proposito, che N e Z sono insiemi discreti. Invece Q, pur avendo “tanti elementi quanti N” (gli elementi di Q possono essere posti in corrispondenza biunivoca con quelli di N e si dice che anche Q è un insieme numerabile), risulta denso nel senso che tra due numeri razionali ne esistono infiniti altri anch’essi razionali. Per esempio, se a e b sono razionali, lo è anche (a + b)/2 (in termini geometrici: il punto medio del segmento di estremi a e b) e una tale costruzione può essere ripetuta quante volte si vuole. L'approssimazione di una misura può essere pertanto migliorata quanto si vuole.

Questa maggiore ricchezza e flessibilità di Q presta però ancora il fianco ad alcune critiche. Da un punto di vista algebrico, se in Q sono sempre possibili le operazioni di addizione, sottrazione, moltiplicazione e divisione, non è sempre possibile calcolare le radici quadrate. Per esempio, non esiste in Q la radice quadrata di 2, ovvero non esiste alcun numero razionale il cui quadrato sia uguale a 2. Altri famosi e classici problemi la cui soluzione non si riesce a esprimere mediante i numeri razionali sono quelli della duplicazione del cubo e della rettificazione della circonferenza. L’inadeguatezza di Q si rivela anche tramite la sua immagine geometrica. L'insieme Q è incapace di rappresentare la continuità di una retta: infatti, se è vero che Q è denso (e rappresenta quindi un innegabile “progresso” rispetto ai precedenti insiemi numerici) è anche vero che è ancora discontinuo, nel senso che tra due numeri razionali distinti, comunque scelti, ci sono, nel loro ordinamento sulla retta, numeri che razionali non sono. Ogni numero razionale determina sulla retta un “taglio” in due semirette, ma non è altrettanto vero che ogni “taglio” individui un punto ad ascissa razionale.

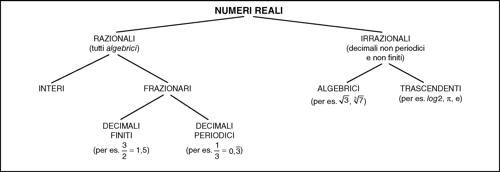
■ I numeri reali. La costruzione dell’insieme R dei numeri reali, ovvero di un insieme numerico che superasse queste inadeguatezze di Q (sempre rispettando il principio di permanenza delle proprietà formali), è avvenuta in tempi relativamente recenti. I numeri irrazionali, quelli che mancano ai razionali per essere un sistema continuo, cominciano a essere introdotti in maniera rigorosa solo nella seconda metà del xix secolo dal matematico francese H.-Ch.-R. Méray e dai tedeschi G. Cantor, H.E. Heine e J.W.R. Dedekind. Quest’ultimo, in particolare, nel volume Stetigkeit und irrationale Zahlen (Continuità e numeri irrazionali, 1872), definisce i numeri reali tramite il concetto di sezione (“taglio”) di Q (si veda → Dedekind, sezione di): «Dal confronto fatto sopra tra il campo dei numeri razionali e la retta siamo stati portati a riconoscere il carattere lacunare, incompleto, la discontinuità del primo, mentre alla retta noi attribuiamo la qualità di essere completa, senza lacune, ossia continua. Ma questa continuità proprio in che cosa consiste? Io vedo l’essenza della continuità [...] nel principio seguente: se una ripartizione di tutti i punti della retta in due classi è di tale natura che ogni punto di una delle classi sta a sinistra di ogni punto dell’altra, allora esiste uno e un sol punto dal quale questa ripartizione di tutti i punti in due classi, o questa decomposizione della retta in due parti è prodotta». Un numero reale viene dunque pensato come sezione di Q, una ripartizione di tutti i razionali in due classi non vuote tali che ogni numero della prima sia minore di ogni numero della seconda. Se la prima classe ammette massimo (o la seconda minimo), il numero reale coincide con questo massimo (o minimo) ed è pertanto un “vecchio” numero razionale, altrimenti l’elemento separatore dà un “nuovo” numero: un numero irrazionale. Con l’insieme R dei numeri reali, unione dei razionali e degli irrazionali, si è nuovamente ottenuto un ampliamento degli insiemi numerici precedentemente conosciuti. È poi a partire dalla definizione di numero reale come sezione di Q che si definiscono le operazioni algebriche in R e si dimostrano le sue principali proprietà: R è un campo totalmente ordinato che permette di risolvere il problema dell’estrazione di radice ed è un insieme che risulta continuo, nel senso che ogni sezione di R individua uno e un solo numero reale separatore che la produce. I numeri reali possono essere rappresentati mediante allineamenti decimali dove, in particolare, l’allineamento risulta finito o periodico per i numeri reali razionali.

L’insieme Rⁿ è il prodotto cartesiano di R per sé stesso n volte: Rⁿ = R × R × ... × R, ovvero è l’insieme delle ennuple ordinate di numeri reali. In particolare R² = R × R è l’insieme delle coppie ordinate di numeri reali, rappresentabile geometricamente sul piano cartesiano. L’insieme R³ = R × R × R è l’insieme delle terne ordinate di numeri reali, rappresentabile geometricamente come insieme dei punti dell’ordinario spazio fisico.

■ I numeri complessi. Le coppie ordinate di numeri reali entrano in gioco quando si definisce l’insieme C dei numeri complessi, l’ultima estensione degli insiemi numerici. Anche la loro introduzione è motivata da un’inadeguatezza, questa volta di R. Come si è visto, infatti, l’insieme dei numeri reali permette di risolvere il problema dell’estrazione della radice quadrata di un numero non negativo, ma in R un numero negativo non ammette radice quadrata (né altra radice di indice pari). Da qui l’estensione a un nuovo insieme, quello dei numeri complessi, attraverso l’introduzione del concetto di numero immaginario, numero complesso con parte reale nulla e quindi della forma iy, dove y è un numero reale e i è l’unità immaginaria: nel piano di Argand-Gauss i numeri immaginari determinano una retta, detta retta immaginaria (sui numeri complessi e sulle loro applicazioni si veda → C, insieme dei numeri complessi).