Il semplice e il complesso dalla fisica alla biologia
Frontiere della Vita (1998)
Il semplice e il complesso dalla fisica alla biologia
The Abdus Salam International Centre for Theoretical Physics, Trieste, Italia
Il semplice e il complesso dalla fisica alla biologia
Il concetto di invarianza di scala e la geometria frattale cambiano il modo di osservare la natura e permettono di estendere il metodo scientifico a fenomeni caratterizzati da irregolarità e complessità intrinseche. La formazione di strutture irregolari in vari processi, i fenomeni di aggregazione, i sistemi geologici, i materiali disordinati e la distribuzione delle galassie nell'Universo sono alcuni dei campi nei quali l'invarianza di scala è stata identificata come elemento comune e fondamentale. Dal punto di vista teorico si comincia a capire in che modo sistemi dissipativi e lontani dall'equilibrio possono portare a comportamenti collettivi di nuovo tipo, con l'emergere di strutture organizzate di grande complessità. Proprietà di invarianza di scala sono state evidenziate anche in molti fenomeni biologici fondamentali. Esempi notevoli si possono trovare in fisiologia, nelle proprietà di autosimilarità degli organismi viventi e nei complessi meccanismi dinamici dell'evoluzione biologica. I moderni concetti della fisica statistica sembrano quindi aprire nuove e originali prospettive in importanti aree della biologia.
Il semplice e il complesso
L'approccio tradizionale della fisica è quello di considerare i sistemi più semplici e di studiarli in grande dettaglio. Questo approccio si focalizza sui 'mattoni' elementari che costituiscono la materia. Da questi studi è stato possibile derivare leggi generali che si applicano in un senso più ampio e che si estendono dalla scala del nucleo atomico a quella delle galassie. In questa prospettiva, l'idea di base è che la conoscenza delle proprietà dei singoli elementi che costituiscono la materia ci permette di capire come si comporti un insieme composto da un gran numero di questi elementi. Questo è l'approccio riduzionistico che si applica con successo in un gran numero di situazioni. È facile però rendersi conto che per una cellula o un organismo vivente la situazione è molto diversa. Cellule e organismi viventi sono fatti di atomi e le proprietà dei singoli atomi sono molto ben conosciute. Ma anche se la nostra conoscenza dell' atomo fosse perfetta, è chiaro che essa non sarebbe sufficiente per comprendere il funzionamento di una cellula. Siamo quindi di fronte a una nuova situazione: la conoscenza delle proprietà degli elementi individuali non è sufficiente per descrivere la struttura nel suo insieme. Il punto è che quando questi elementi interagiscono tra di loro formano delle strutture complesse e sviluppano delle funzioni che hanno poco a che fare con le proprietà dei singoli componenti isolati. Possiamo rappresentare questa situazione come lo studio della 'architettura' della materia e della natura. Essa dipende in qualche modo dalle proprietà dei 'mattoni', ma possiede poi caratteristiche e leggi fondamentali che non possono essere ricollegate a quelle dei singoli elementi. Inoltre, per la biologia c'è anche da considerare il ruolo essenziale della storia specifica che ha portato allo sviluppo della vita sulla Terra. La biologia si focalizza su tale sviluppo, studiando il modo in cui esso è effettivamente avvenuto e gli organismi viventi come sono realmente. Dal punto di vista della fisica, invece, si tende a considerare il processo reale come una delle possibilità di un'intera classe di processi simili. Malgrado queste profonde differenze, è ragionevole aspettarsi che i nuovi concetti della moderna fisica statistica possano avere un ruolo importante nella comprensione delle proprietà e dell'emergenza spontanea di strutture complesse in biologia. Il concetto di sistema complesso, sebbene molto usato recentemente, non è ancora definito con precisione nella letteratura scientifica e può generare confusione. Ciò è in parte dovuto al fatto che il campo si sta evolvendo rapidamente. Per ora utilizzeremo questo termine in modo generico; il suo significato diverrà più chiaro in seguito. Le forme più semplici di strutture complesse sono quelle che derivano direttamente dalle leggi fondamentali della fisica in situazioni con molti elementi interagenti e con una dinamica dissipativa. Esempi di questo tipo sono le strutture frattali più familiari, come gli alberi, le linee delle coste, le nuvole, i fulmini, la turbolenza nei fluidi e persino la distribuzione delle galassie nell'Universo (Mandelbrot, 1983; Pietronero e Tosatti, 1986; Evertsz et al., 1996). In questi casi, la complessità è spesso rappresentata dalle proprietà di invarianza di scala che descriveremo in seguito in maggior dettaglio. Il fatto notevole è che queste proprietà emergono spontaneamente dalla dinamica del sistema senza particolari aggiustamenti: in questo senso si parla di sistemi autoorganizzati. Una situazione molto più complessa è quella della biochimica dei sistemi viventi. Le leggi della biologia sono certamente basate su quelle della fisica e della chimica ma con in più altri, importantissimi elementi. Lo sviluppo della vita e il processo dell'evoluzione dipendono infatti in modo cruciale dalla storia specifica del sistema. l sistemi viventi imparano dall' esperienza e possono quindi essere considerati come sistemi complessi adattativi (Gell-Mann, 1994). In questo senso sono diversi dai sistemi complessi non adattativi menzionati prima, che sono quelli più comunemente studiati in fisica. Vi sono comunque delle importanti connessioni tra queste due classi. Negli ultimi anni sono stati formulati modelli di evoluzione biologica relativamente semplici, ispirati ai modelli fisici, che contengono alcuni elementi di adattamento (Kauffman, 1993). Inoltre, è ragionevole ipotizzare che lo sviluppo della vita necessiti della presenza di un ambiente complesso (intermedio tra ordine e disordine) che porti a una sufficiente varietà di possibilità necessarie per l'adattamento e per un'evoluzione efficace. In questa prospettiva la complessità non adattativa fornisce l'ambiente necessario per la complessità adattativa.
Recenti sviluppi della fisica statistica
Dai fenomeni critici alla invarianza di scala generalizzata
La fisica statistica sta attraversando un periodo di profonda trasformazione. L'introduzione di nuove idee, ispirate alla geometria frattale e allo scaling (proprietà di scala), insieme allo studio di processi dissipativi con proprietà di autoorganizzazione, hanno portato a un notevole arricchimento del quadro tradizionale e hanno fornito metodi nuovi per caratterizzare e comprendere i sistemi complessi. Si tratta dunque di un campo nuovo che include contenuti di varie discipline che vanno dalla fisica della materia alla geologia, alla biologia, all'astrofisica e all'economia (Evertsz et al., 1996). Tale interdisciplinarità dipende dal fatto che queste idee ci permettono di guardare ai fenomeni naturali in un modo originale, ispirato a concetti unificanti, indipendentemente dalla struttura dettagliata del sistema. L'interesse in questo campo è dovuto per lo più a due fattori. Il primo è legato allo sviluppo di calcolatori molto potenti, grazie ai quali è divenuto possibile effettuare simulazioni dettagliate di molti sistemi complessi; il secondo al fatto che il linguaggio matematico adatto a descrivere questi fenomeni dissipativi e lontani dall' equilibrio è diventato accessibile solamente negli ultimi anni. Lo studio dei fenomeni critici nelle transizioni di fase continue ha introdotto nella fisica il concetto di scaling e il comportamento a legge di potenza con esponenti critici. La geometria frattale (Mandelbrot, 1983) ha fornito il quadro matematico per l'estensione di questi concetti a una vasta gamma di fenomeni naturali.
La fisica dei sistemi complessi autoorganizzati ha però evidenziato aspetti nuovi rispetto ai fenomeni critici. La teoria dei sistemi in equilibrio termodinamico si basa fortemente sull'ipotesi ergodica, che consiste nell'assumere che la dinamica del sistema esplori lo spazio delle fasi in modo uniforme; questa ipotesi permette di evitare lo studio dettagliato della dinamica e di descrivere le proprietà di equilibrio termodinamico direttamente in termini di proprietà medie dello spazio delle fasi. L'invarianza di scala si sviluppa esattamente al punto di equilibrio critico tra ordine e disordine e il raggiungimento di questo equilibrio necessita di un delicato aggiustamento dei parametri del sistema. Al contrario, la maggior parte dei fenomeni invarianti di scala osservati in natura è auto organizzata, nel senso che tali fenomeni si generano spontaneamente da un processo dinamico irreversibile. Siamo quindi portati a ricercare le origini della invarianza di scala generalizzata nella vasta area dei sistemi dissipativi e fuori dall' equilibrio e questo richiede lo sviluppo di nuove idee e metodi.
Tre livelli di comprensione
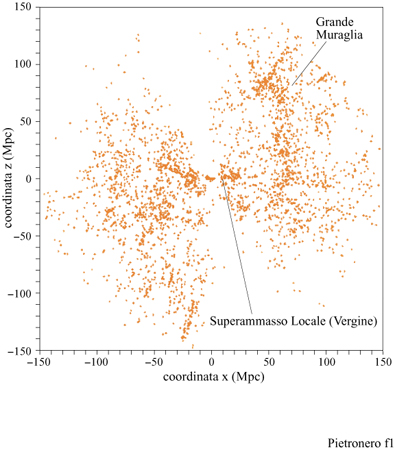
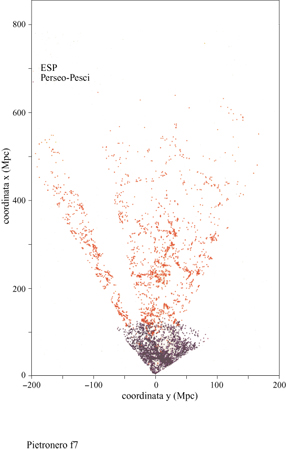
Rendersi conto che certe strutture in natura hanno proprietà frattali non spiega perché questo accada, ma è fondamentale per formulare le domande appropriate. L'impatto dei frattali in fisica può essere collocato a tre diversi livelli di comprensione: 1) la geometria frattale come una nuova matematica che conduce alla rianalisi di fenomeni e di dati noti, producendo spesso un sovvertimento di punti di vista consolidati. Questo permette di includere nelle aree scientifiche molti fenomeni caratterizzati da irregolarità intrinseche, finora trascurati a causa della mancanza di metodi matematici appropriati. Per esempio, la distribuzione delle galassie nell 'Universo (fig. 1) e la crescita di una colonia di batteri sono casi nei quali analisi statistiche dettagliate hanno permesso di identificare proprietà frattali.
2) La formulazione di modelli fisici per sistemi che mostrano proprietà frattali e di autoorganizzazione. Da un punto di vista matematico spesso questi modelli sembrano relativamente semplici e consistono in processi iterativi non lineari. Essi però danno luogo a sistemi con caratteristiche e proprietà estremamente complesse, generate spontaneamente dalla dinamica del sistema. Le simulazioni numeriche rappresentano uno strumento essenziale per esplorare queste proprietà. La maggior parte di queste simulazioni è basata su modelli fortemente idealizzati e utilizzati a volte come semplici metafore. È importante rendere questi modelli più realistici e vicini ai fenomeni naturali; questo rappresenta l'attuale frontiera del campo. La figura (fig. 3) mostra i risultati di una simulazione di uno dei più interessanti modelli di crescita frattale, l'aggregazione limitata dalla diffusione, che discuteremo in seguito.
3) La costruzione di teorie fisiche complete che permettano di capire l'origine auto organizzata delle strutture frattali e delle altre proprietà dei sistemi fisici complessi. Una delle principali difficoltà è rappresentata dal fatto che la dinamica temporale è intrinsecamente irreversibile e non può essere eliminata da una qualche forma di ipotesi ergodica. Nella meccanica statistica dell'equilibrio, l'ipotesi ergodica permette di eliminare l'evoluzione dinamica specifica e di assegnare direttamente un peso statistico (probabilità) di Boltzmann a una data configurazione. Nel caso delle strutture frattali questo normalmente non è possibile ed è necessario conoscere la storia dinamica completa del sistema per poter definire il peso statistico di una data configurazione. Questo implica lo sviluppo di concetti teorici di nuovo tipo che tengano in particolare considerazione gli aspetti della dinamica irreversibile.
Strutture regolari e irregolari: l'invarianza di scala
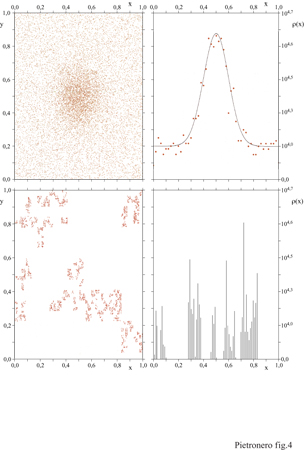
La maggior parte della fisica teorica si basa su funzioni regolari e su equazioni differenziali. Ciò vuoI dire che le strutture sono essenzialmente regolari e le irregolarità sono trattate come fluttuazioni o singolarità isolate. Lo studio dei fenomeni critici e lo sviluppo della teoria del gruppo di rinormalizzazione (RG, Renormalization Group) negli anni Settanta hanno notevolmente ampliato il nostro quadro concettuale (Amit, 1978; Wilson, 1983). Finalmente si possono descrivere e comprendere fenomeni nei quali irregolarità intrinseche e autosimili si sviluppano su qualsiasi scala e in cui le fluttuazioni non possono essere formulate in termini di espressioni analitiche (fig. 4). Il motivo per cui i metodi teorici adatti a descrivere queste situazioni non possono basarsi sulle normali equazioni differenziali consiste nel fatto che l' autosimilarità comporta l'assenza di analiticità, che è invece essenziale per gli usuali metodi matematici della fisica. In un certo senso, l'RG corrisponde alla ricerca di uno spazio nel quale il problema diventa di nuovo analitico. Questo è lo spazio delle trasformazioni di scala, non lo spazio ordinario, nel quale le fluttuazioni sono molto irregolari. Per un certo periodo di tempo queste situazioni peculiari sembravano essere limitate allo specifico punto critico che corrisponde all'equilibrio nella competizione tra ordine e disordine. Al contrario, negli ultimi anni si è chiarito che una grande varietà di strutture presenti in natura sono intrinsecamente irregolari e auto simili.
La principale differenza tra le forme frattali più conosciute, come coste, montagne, alberi, nuvole, fulmini, ecc., e la autosimilarità dei fenomeni critici è che la criticità nelle transizioni di fase si ha soltanto con un aggiustamento fine ed estremamente sensibile dei parametri critici, quale per esempio la temperatura. Nelle strutture frattali osservabili in natura, invece, le proprietà critiche sono auto organizzate, cioè si sviluppano spontaneamente dal processo dinamico stesso senza particolari aggiustamenti. Lo sviluppo dei fenomeni critici e della geometria frattale sono stati abbastanza indipendenti, per lo meno all'inizio, proprio a causa di questa importante differenza. Il fatto di pensare tradizionalmente in termini di strutture analitiche e regolari ha delle conseguenze cruciali sul tipo di domande che ci poniamo e sui metodi con cui tentiamo di dare delle risposte. L'estensione dei concetti matematici alle situazioni irregolari e non analitiche ci porta a una visione notevolmente diversa di molti fenomeni naturali, sia dal punto di vista teorico sia da quello sperimentale.
Proprietà dei frattali: semplici ma sorprendenti
Cenni storici
Verso la fine del 19° secolo, diversi matematici studiarono certi insiemi e funzioni che sono continui ma non differenziabili: l'insieme di Cantor, l'intreccio di Sierpinski, l'insieme di Julia, ecc. (Mandelbrot, 1983). Un elemento comune di questi insiemi è che essi sono auto simili, cioè mostrano lo stesso tipo di struttura a diverse scale. In questi sistemi le lunghezze o le aree sono mal definite e dipendono dall 'unità di misura utilizzata, come nel caso della parte inferiore della figura 4. Successivamente, F. Hausdorff riconobbe che si poteva assegnare una dimensione frazionaria a questi insiemi. Nella fisica questi concetti sono rimasti in gran parte trascurati, tranne poche eccezioni, come quella di J.-B. Perrin, il quale notò che la maggioranza dei profili in natura è effettivamente non differenziabile, e che la loro lunghezza è mal definita. O.W. Richardson nel 1926 descrisse la turbolenza nei fluidi in termini di strutture vorticose auto simili e nel 1941 A.N. Kolmogorov fu ispirato dall'idea della frammentazione auto simile per formulare la sua teoria della turbolenza, nella quale però la dissipazione d'energia viene assunta come omogenea nello spazio.
B. Mandelbrot (1983) si rese conto che l'autosimilarità e le curve non differenziabili sono comuni in natura e che le cosiddette funzioni patologiche, di dimensione frazionaria, costituiscono un linguaggio matematico appropriato per la loro descrizione. In tale prospettiva introdusse il concetto di geometria frattale (dal latino fractus, frammentato) e propose questa come potente mezzo matematico per lo studio scientifico degli oggetti e dei fenomeni complessi nel mondo della fisica. Le montagne, gli alberi, i profili delle coste, i fulmini, le turbolenze nei fluidi, la distribuzione delle galassie ma anche gli errori di trasmissione nei sistemi telefonici, le strutture statistiche nel linguaggio, il polmone umano e addirittura le fluttuazioni economiche in borsa sono esempi nei quali proprietà frattali sono state analizzate e caratterizzate quantitativamente. La geometria frattale ci permette quindi di espandere le frontiere delle discipline scientifiche, includendo tutti quei fenomeni che sono caratterizzati da irregolarità intrinseche e auto simili. Questa nuova situazione cambia il nostro modo di guardare la natura, che si presenta ora più ricca e affascinante.
Invarianza di scala e leggi di potenza
È utile analizzare qualche proprietà essenziale delle strutture frattali. Consideriamo un oggetto come un insieme di punti definiti in uno spazio euclideo di dimensione d. Usiamo uno di questi punti come origine e contiamo il numero di punti N(R) compresi entro una certa distanza R. Se l'oggetto è euclideo avremo N(R) =Rd. Per un oggetto frattale (v. figura 4, in basso) si trova ancora una legge di potenza che lega la 'massa' dell'insieme di n punti e la sua lunghezza R, ma in questo caso N(R) =RD,, dove D (dimensione fra tta le ) non è un numero intero e può assumere un valore compreso tra 0 e d. Da questo segue che la densità media condizionale dei punti, che corrisponde alla probabilità di trovare un punto a distanza R da un altro punto posto nell'origine, è n(R) =N(R)/Rd =R-(d-D) (Mandelbrot, 1983; Vicsek, 1992). Riassumendo, gli oggetti frattali hanno una densità che decade con una legge di potenza in relazione alla loro grandezza, quindi non è possibile definire in modo appropriato una densità media. Come confronto, in un solido o in un liquido la densità condizionale a piccola distanza consiste in un insieme di picchi che corrispondono alle posizioni degli atomi vicini; a maggiore distanza la densità di questi picchi tende a un valore costante che defrnisce la densità media del sistema. Al contrario, per un frattale la densità varia con una legge di potenza a tutte le scale e decade gradualmente verso zero. Questo implica che, su grande scala, le regioni vuote saranno prevalenti e le strutture diventeranno molto sparse. Inoltre, le leggi di potenza per le correlazioni si riferiscono a una media statistica. Una struttura specifica, caratterizzata da invarianza di scala, mostra sempre grandi fluttuazioni e la presenza di strutture e di vuoti di ogni grandezza. Nella discussione precedente abbiamo considerato le conseguenze geometriche della autosimilarità. Vediamone ora le implicazioni matematiche. Consideriamo una funzione Γ(r) che descrive qualche proprietà del sistema. Per esempio, tale proprietà può essere la correlazione o la distribuzione dei vuoti in funzione della distanza r. La correlazione descrive il modo in cui il fatto che un dato punto sia parte della struttura influenza la probabilità che un altro punto a distanza r sia anch'esso parte della struttura. La trasformazione di scala di un fattore b corrisponde alla sostituzione della lunghezza r con br e alla nuova funzione Γ(br). La condizione della invarianza di scala richiede che le due funzioni siano identiche, a parte un fattore costante A che dipende da b ma non da r. Cioè Γ(br) =A(b)Γ(r). È facile verificare che le leggi di potenza sono la soluzione naturale di questa equazione funzionale. Infatti, se Γ(r) =rα, abbiamo Γ(br) = bαΓ(r). Questo implica che l'osservazione di leggi di potenza nelle proprietà di un sistema fornisce una diretta indicazione delle sue proprietà di invarianza di scala.
L'Universo frattale
Argomenti tradizionali
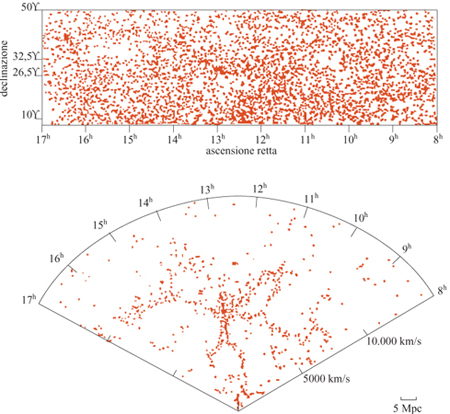
In questo paragrafo discutiamo un esempio in cui i nuovi concetti della geometria frattale rivelano nuove proprietà della struttura a larga scala dell 'Universo e conducono a nuove prospettive, affascinanti e controverse allo stesso tempo. Prima delle numerose misure di redshift degli anni Ottanta (le quali forniscono una misura della distanza assoluta), la distribuzione delle galassie era conosciuta solo rispetto alle due coordinate angolari che individuano la posizione della galassia rispetto al piano galattico. Queste distribuzioni angolari apparivano piuttosto regolari su scale angolari relativamente grandi, come si può osservare in figura (fig. 5) in alto. Assumendo che questa regolarità corrisponda a una reale omogeneizzazione nello spazio tridimensionale, è stata stimata una lunghezza caratteristica ro pari a 5 Mpc (Peebles, 1980; 1993), dove lMpc = 3,26.10⁶ anni-luce. Il raggio dell'Universo intero è di circa 4000 Mpc, mentre la grandezza di una singola galassia - un punto nella nostra discussione - è 0,01÷ 0,1 Mpc. L'idea era che oltre questa distanza la distribuzione diventasse gradualmente omogenea e potesse essere definita da una densità costante di galassie. Questo valore, a parte l'eventuale ruolo della materia oscura, sarebbe quello da utilizzare nelle equazioni di Einstein per lo studio della metrica, il modello del Big Bang, ecc. In seguito, le misure dei redshift delle galassie, insieme alla legge di Hubble (v. il saggio di M. Hack, La struttura dell'Universo), hanno permesso di definire le distanze assolute e di identificare la posizione delle galassie nello spazio. La distribuzione tridimensionale delle galassie si è rivelata molto più irregolare rispetto alla sua proiezione angolare, risultando caratterizzata da grandi strutture e grandi vuoti, come mostrano la parte inferiore della figura 5 e la figura 1. In un primo momento queste strutture irregolari sembravano essere in contraddizione con le conclusioni ottenute dai cataloghi angolari. In seguito, però, le correlazioni studiate anche per questi cataloghi tridimensionali sembravano confermare il risultato precedente, ro = 5 Mpc. Questo portava alla curiosa conclusione che una lunghezza di correlazione relativamente piccola potesse essere compatibile con strutture e vuoti molto più grandi. Il problema consiste nel fatto che, di solito, l'analisi delle correlazioni viene fatta stimando la distanza ro alla quale le fluttuazioni di densità sono comparabili alla densità media. In pratica, ciò si fa considerando la funzione
ζ(r) = ⟨n(O)n(r)⟩ / ⟨n⟩2 -1,
dove n(r) rappresenta la densità dei punti occupati, e si defrnisce la lunghezza caratteristica ro come la distanza a cui ζ(ro) = l (Peebles, 1980; 1993). Il punto è che questa procedura è corretta se il sistema diventa realmente omogeneo all'interno del catalogo considerato. Se invece le correlazioni frattali si estendono sino ai limiti del campione, allora il valore ottenuto per ro non ha nulla a che vedere con le proprietà reali della distribuzione delle galassie, ma viene determinato dalla grandezza del volume del campione Rs (Coleman e Pietronero, 1992).
Nuove prospettive
La conseguenza delle considerazioni precedenti è che gli studi tradizionali della correlazione in termini della funzione ζ(r) non possono chiarire tali questioni, perché l'omogeneità è assunta a priori. L'analisi appropriata delle correlazioni deve quindi usare metodi che siano in grado di distinguere le proprietà omogenee o frattali senza scelte a priori. Il metodo più semplice è di considerare direttamente la densità condizionale
Γ(r) = ⟨n(O)n(r)⟩
senza confrontarla con la densità media. Però questo non è tutto, perché bisogna anche evitare assunzioni implicite di omogeneità nel trattamento delle condizioni al contorno (Coleman e Pietronero, 1992). Per queste ragioni, la validità statistica di un campione è limitata al raggio Rs della sfera più grande che può esservi contenuta.
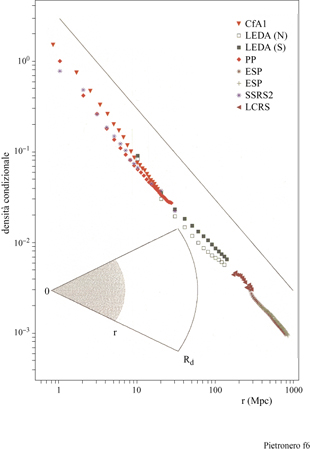
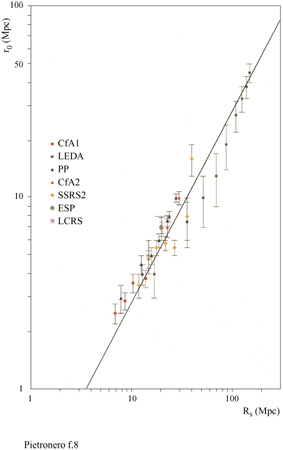
I dati principali della nostra analisi delle correlazioni sono illustrati in figura (fig. 6), dove riportiamo la densità condizionale in funzione della distanza per diversi cataloghi di galassie (Pietronero et al., 1997; Sylos Labini et al., 1998). Le proprietà derivate dai diversi cataloghi sono compatibili tra loro e dimostrano un decadimento a legge di potenza (correlazioni frattali) per la densità condizionale da 1 Mpc a 150 Mpc, senza la tendenza verso una omogeneizzazione o un appiattimento delle correlazioni. Usando anche altri dati relativi a galassie più lontane (fig. 7), per i quali però l'analisi ha alcune limitazioni statistiche, è possibile osservare che il comportamento frattale continua fino a 1000 Mpc (Sylos Labini et al., 1998). Il comportamento globale osservato corrisponde a una struttura frattale di dimensione D pari a circa 2 (precisamente tra 1,8 e 2,2). Una distribuzione omogenea corrisponderebbe a un appiattimento della densità condizionale che non è mai stato osservato. Questi risultati implicano che il valore di ro (derivato dall' approccio usuale) non rappresenta la vera lunghezza di correlazione ma dipende direttamente dalla profondità del campione considerato, come mostrato in figura (fig. 8). Si può osservare che il valore di ro va da 5 a quasi 50 Mpc a mano a mano che si estende la profondità dei campioni. I metodi statistici tradizionali, basati sull' assunzione di omogeneità (Peebles, 1980; 1993), appaiono quindi inconsistenti per tutte le scale di lunghezza finora accessibili. È necessario uno schema concettuale più generale per identificare le reali proprietà fisiche di queste strutture e le teorie devono quindi rivolgersi agli esponenti piuttosto che all'ampiezza della correlazione, nel senso discusso in precedenza. La distribuzione della materia visibile nell'Universo è quindi frattale e non omogenea fino ai presenti limiti osservativi. Inoltre, la distribuzione della luminosità è correlata alla distribuzione nello spazio in un modo molto specifico, caratterizzato da proprietà multifrattale (Sylos Labini et al., 1998). Questi fatti hanno delle implicazioni concettuali affascinanti riguardo alla nostra conoscenza dell'Universo e aprono un nuovo scenario con nuove sfide teoriche. In particolare, il principio cosmo logico (PC) di S.E. Weinberg (1972) può essere considerato in una prospettiva più ampia. Tradizionalmente, la richiesta di non considerarci in un punto privilegiato dell'Universo è stata interpretata come equivalente all'assunzione di omogeneità (Peebles, 1993). Questo è corretto se ci si limita alle distribuzioni analitiche (regolari). In un frattale tutti i punti sono statisticamente equivalenti e soddisfano in questo senso il PC; vi è però un'asimmetria tra i punti occupati e le regioni vuote e la struttura non è omogenea a nessuna scala.
Modelli fisici per la crescita frattale e l'autoorganizzazione
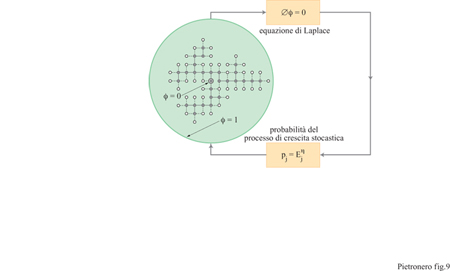
Dopo aver verificato che molte strutture in natura sono auto simili è naturale domandarsi perché la natura produca queste strutture frattali. Il primo modello fisico con il quale si iniziò a chiarire questo problema è il modello DLA (Diffusion Limited Aggregation, aggregazione limitata dalla diffusione), formulato da T.A. Witten e L.M. Sander (1981), che produce strutture complesse come quella già incontrata nella figura 3. Il modello è ispirato dall'osservazione che alcuni aggregati in fase gassosa (per esempio, il fumo) mostrano una struttura frattale. Si inizia con una particella fissa in un dato punto (nominalmente definito come centro) e si introduce a una determinata distanza R (abbastanza grande) una nuova particella che esegue un moto browniano su un reticolo (diffusione). Quando questa particella arriva in un sito adiacente al centro, essa viene congelata in questa posizione e la struttura dell'aggregato si estende. Viene allora introdotta una nuova particella che raggiunge un altro sito adiacente al nuovo aggregato e così via. L'iterazione di questo semplice algoritmo produce spontaneamente delle strutture di grande complessità con una dimensione frattale D = 1,7 (per la crescita in un piano). Successivamente, L. Niemeyer e collaboratori (1984) introdussero il modello DBM (Dielectric Breakdown Model, modello del breakdown dielettrico), ispirato dalle scariche nei gas (per esempio i fulmini). Si assume che la struttura dove il breakdown è già avvenuto sia equipotenziale. Partendo dall' equazione di Laplace è possibile calcolare il campo elettrico locale per tutti i segmenti intorno alla struttura stessa. La probabilità di crescita per ogni segmento si assume proporzionale al campo elettrico locale. Un segmento viene selezionato in modo probabilistico e diventa parte della nuova struttura, come indicato in figura (fig. 9).
Il processo dinamico DBM, oltre a generare strutture tipo DLA, ne chiarisce le proprietà matematiche in relazione alle equazioni alle derivate parziali. Questi frattali, detti fra tta li laplaciani, 'catturano' le proprietà frattali essenziali di vari fenomeni come la deposizione elettro chimica, il breakdown dielettrico, le interfacce tra liquidi viscosi, la propagazione delle fratture e varie proprietà dei colloidi (Vicsek, 1992). In figura (fig. 10) è riportata una struttura DBM che cresce da una linea invece che da un punto. Questa geometria è più interessante per una descrizione teorica poiché corrisponde a un'unica direzione di crescita. Le strisce intorno alle strutture corrispondono alle linee equipotenziali ottenute risolvendo l'equazione di Laplace. Ogni coppia di strisce corrisponde a una diminuzione del potenziale (e quindi della probabilità di crescita) di un fattore 10.
Una variante interessante del DLA è il modello di aggregazione di tipo cluster-cluster (Vicsek, 1992), nel quale il processo di aggregazione inizia con molte particelle che seguono moti browniani e che possono aggregarsi in cluster I di ogni dimensione, i quali si muovono anch'essi e si aggregano, e così via. Ogni cluster si rivela frattale con una dimensione inferiore rispetto al modello DLA. Inoltre, la distribuzione delle dimensioni dei cluster mostra un comportamento a legge di potenza. Il modello cluster-cluster riesce a descrivere sistemi quali la polvere, il fumo e i colloidi (Weitz e Oliveria, 1984), come mostrato in figura (fig. 11).
Il concetto della generazione spontanea di strutture complesse o critiche, detto anche SOC (Self-Organized Criticality, criticalità auto organizzata), è stato recentemente analizzato in modo approfondito nei modelli di tipo sandpile (letteralmente, mucchio di sabbia) introdotti da P. Bak e collaboratori (1987). Per illustrare l'idea del meccanismo SOC si considera un modello di automa cellulare ispirato alle proprietà di un mucchietto di sabbia. L'aggiunta casuale di granelli di sabbia porta il sistema verso uno stato stazionario, con una distribuzione di valanghe che risulta invariante di scala. Come nel modello precedente per la crescita frattale, anche in questo la criticalità o invarianza di scala (cioè la competizione critica fra ordine e disordine) sembra emergere automaticamente, senza l'aggiustamento di parametri. Data la loro importanza concettuale, queste idee sulla auto organizzazione hanno invaso rapidamente le scienze, dalla fisica e dalla geofisica alla biologia e all'economia, fornendo un meccanismo prototipo per capire il manifestarsi dell'invarianza di scala e della complessità nei fenomeni naturali.
Verso una comprensione teorica
I modelli discussi nella sezione precedente illustrano ben precise situazioni fisiche che conducono alla generazione di strutture frattali. Un confronto con i dati sperimentali suggerisce infatti che questi modelli descrivono la fisica essenziale di vari fenomeni con proprietà frattali. Tuttavia, essi non costituiscono ancora una teoria e questo sarà il prossimo punto della nostra discussione. Una teoria necessita di una comprensione precisa del ruolo dei diversi elementi dei modelli, la classificazione delle loro proprietà e la possibilità di predire analiticamente il loro comportamento indipendentemente dalle simulazioni al calcolatore.
Dal punto di vista teorico, l'idea di molti autori è che DLA, DBM e altri modelli SOC pongano delle questioni di nuovo tipo per le quali sarebbe auspicabile avere uno schema teorico comune (Kadanoff, 1990; 1991). I tentativi di usare i concetti teorici sviluppati per fenomeni critici, come la teoria dei campi e il gruppo di rinormalizzazione, sono stati abbastanza problematici per questi nuovi fenomeni. Le differenze di fondo rispetto alle transizioni di fase di equilibrio sono che, nei modelli in esame, la dinamica è irreversibile e autoorganizzata. Non esiste un principio ergodico e non è possibile assegnare un peso statistico di Boltzmann a una configurazione senza conoscere la storia completa della sua crescita. Nella tabella (tab. I) sono illustrate le proprietà e le questioni principali relative ai fenomeni critici usuali, rappresentati dal modello di Ising, messe a confronto con quelle relative ai nuovi modelli critici autoorganizzati, rappresentati da DLA, DBM e dal modello sand pile. Si può osservare che, a parte la comune proprietà dell'invarianza di scala, la situazione è, in realtà, molto diversa.
Per il modello di Ising l'ergodicità è una proprietà fondamentale, perché elimina la dinamica temporale dall' analisi statistica. Nei nuovi modelli, invece, la dinamica temporale irreversibile è cruciale e in questo senso essi sono concettualmente più vicini alle problematiche biologiche. L'autoorganizzazione è un'altra caratteristica dei nuovi modelli. Nel modello di Ising invece la criticità avviene soltanto aggiustando accuratamente la temperatura critica e solamente al punto critico la lunghezza di correlazione ζ diverge.
Lo sforzo teorico in questo campo può essere diviso in teorie fenomeno logiche o di scaling e teorie microscopiche. Il primo approccio è stato sviluppato ampiamente negli ultimi anni e consiste nella definizione di relazioni di consistenza tra le assunte proprietà di scaling del sistema. Questo approccio fenomenologico è essenziale nell'analisi delle simulazioni numeriche per identificare ed estrapolare le informazioni essenziali del problema. L'approccio microscopico consiste invece nella comprensione di tutte le proprietà SOC e frattali del sistema direttamente dalla conoscenza della sua dinamica microscopica. Questo ci porta al problema cruciale dell' origine dei frattali. Abbiamo visto che la maggior parte dei modelli di crescita frattale come DLA, DBM, aggregazione cluster-cluster e modelli sand pile, a causa della loro irreversibilità e auto organizzazione, pongono una problematica teorica di nuovo tipo. Un tentativo di costruire una teoria fisica per i frattali auto organizzati con dinamiche irreversibili è la FST (Fixed Scale Transformation, trasformazione a scala fissa). Questo approccio (Erzan et al., 1995) permette di capire l'origine dell' auto organizzazione nella crescita frattale in termini di un punto fisso attrattivo per la dinamica invariante di scala e di calcolare analiticamente la dimensione frattale. Al momento la FST sembra essere l'unico approccio generale per l'ampia gamma dei frattali auto organizzati e dei modelli sand pile (Pietronero et al., 1994). Nonostante questi progressi, molte importanti questioni rimangono aperte. L'obiettivo futuro è di sviluppare queste idee nell'ambito di un quadro teorico generale e sistematico con una capacità predittiva in relazione alla crescita frattale e alle proprietà SOC.
L'universalità nei frattali
Un argomento cruciale è il ruolo dell'universalità nei frattali e nei fenomeni SOC. Nei fenomeni critici usuali gli stessi esponenti che definiscono le transizioni di fase magnetiche descrivono anche la transizione liquido-vapore nell'acqua al punto critico (dove la transizione è continua). Questa forte universalità sembra essere una caratteristica dei sistemi all'equilibrio. l sistemi auto organizzati invece non sembrano esibire lo stesso grado di universalità poiché il valore della dimensione frattale può modificarsi in seguito a cambiamenti relativamente semplici nel processo di crescita. Questa universalità ridotta è a volte considerata come un elemento negativo, perché ci costringe a descrivere ogni sistema specifico invece di un singolo modello universale. Questa prospettiva però può essere ribaltata nel modo seguente. Alcuni concetti teorici sono probabilmente generali o universali, ma rispetto ai fenomeni critici usuali la diversità dei vari modelli che abbiamo considerato diventa un elemento di ricchezza e di interesse specifico. Dopotutto, le strutture SOC e frattali che osserviamo in natura sono molto varie e diverse tra loro. La conoscenza preliminare che abbiamo al momento ci suggerisce che esistono alcuni principi universali, ma le proprietà specifiche dipendono dal processo specifico. È possibile che questo abbia a che fare con il fatto che il dominio dei fenomeni irreversibili è molto più ampio di quello dei fenomeni di equilibrio. La definizione delle classi e delle leggi per questa nuova area è certamente uno degli obiettivi principali della attività teorica in questo campo.
Dalla fisica alla biologia
La complessità in fisica
L'approccio riduzionistico in fisica è stato essenziale per la derivazione di leggi generali che si applicano dal nucleo atomico alla struttura delle galassie. l problemi aperti a questo riguardo nascono al di sotto della scala dei quark e nella cosmologia al di sopra della scala delle galassie. La biologia si trova completamente all'interno di questa regione conosciuta, ma le leggi fondamentali della fisica non sono sufficienti per derivare le proprietà dei biosistemi. Il punto è che già all'interno della fisica queste leggi non possono spiegare direttamente molti dei fenomeni che abbiamo visto precedentemente. Un esempio ancora più semplice viene dalla termodinamica. La conoscenza delle traiettorie di tutti gli atomi di un gas non ci porta necessariamente al concetto di entropia né alle leggi della termodinamica di Boltzmann e Gibbs. La comprensione del comportamento del gas richiede l'introduzione di nuovi concetti che si riferiscono alle proprietà medie del sistema. Questi concetti termodinamici hanno le loro proprie leggi fondamentali che si possono ricollegare, ma solo in modo remoto, alle leggi della dinamica microscopica.
Lo sviluppo di potenti mezzi di calcolo numerico è di grande aiuto per lo studio di situazioni ben controllate. È però fondamentale in questi studi numerici formulare le domande più appropriate e significative e per questo motivo bisogna prima identificare i concetti rilevanti. Per esempio, la familiare transizione di fase tra lo stato solido e quello liquido è tuttora compresa in modo incompleto. l calcolatori ci permettono di riprodurla, ma i suoi principi generali e le sue proprietà sono ancora non completamente chiariti.
Lo studio dei fenomeni critici ha rappresentato un grande passo avanti nel capire in quale modo le proprietà di invarianza di scala si originano dal comportamento collettivo di tanti elementi in interazione tra loro. La crescita frattale e la auto organizzazione hanno messo in luce molte proprietà sorprendenti e affascinanti dei sistemi dinamici dissipativi. In modo particolare la loro dinamica irreversibile comincia ad avere qualche somiglianza con alcuni problemi della evoluzione biologica. Altri campi dei quali non discuteremo in questa sede, ma che potrebbero avere proprietà di interesse biologico, sono i cosiddetti vetri di spin (spin glass) e il caos deterministico. l modelli dei vetri di spin (Mezard et al., 1987) studiano sistemi con interazioni in competizione tra loro che conducono a molti stati metastabili per il sistema globale. Il caos deterministico si riferisce a un comportamento erratico dei sistemi dinamici non lineari che diventano essenzialmente imprevedibili in certi intervalli di valore dei parametri che caratterizzano la loro dinamica.
Queste nuove aree rappresentano la frontiera della fisica statistica moderna e studiano problemi che sono usualmente definiti come complessi. Con questo termine ci riferiamo a sistemi in cui un comportamento collettivo strutturato emerge spontaneamente dalla dinamica irreversibile o dissipativa ed è, in questo senso, dipendente dalla storia. Come abbiamo visto, nella maggior parte dei casi questo comportamento complesso è associato spesso a proprietà di invarianza di scala.
Fisica e biologia
Una parte della biologia appare come un'affascinante palestra per lo studio dei sistemi complessi auto organizzati. Comunque, vi sono ancora notevoli barriere concettuali, in quanto la fisica e la biologia si basano su prospettive diverse. La fisica cerca di semplificare e di idealizzare sistemi e fenomeni con l'obiettivo di formulare leggi generali; la biologia studia la realtà per come è e le sue domande sono rivolte alle strutture e ai processi specifici degli organismi viventi. In questo senso è una disciplina storica, dipende dalle leggi della fisica ma anche dall'enorme quantità di informazioni che si sono accumulate attraverso il meccanismo specifico dell'evoluzione avvenuto sulla Terra. In quest'ottica potrebbe anche dipendere da specifici eventi storici. Una delle caratteristiche principali dell'evoluzione biologica è la capacità di apprendere dall'esperienza; dunque, la biologia studia sistemi complessi di tipo adattativo. Questa caratteristica va oltre i sistemi complessi usualmente studiati in fisica, ma fra poco vedremo che è possibile fare qualche passo anche in questa direzione. Normalmente l'adattamento richiede una combinazione di ordine e disordine in un modo che richiama il concetto di criticità e invarianza di scala. Il punto cruciale è capire come strutture ben organizzate di tipo adattativo possano emergere spontaneamente dalla dinamica dissipativa di un sistema complesso.
Le dinamiche irreversibili pongono il problema della freccia del tempo. Questa è definita dalla condizione iniziale e dalla dinamica stessa dell'Universo il quale è, globalmente, fuori dall'equilibrio. Il fatto che questa dinamica tenda a un limite deterministico è conseguenza sia delle leggi della meccanica quantistica sia delle proprietà caotiche delle dinamiche non lineari.
L'emergere di organismi viventi ordinati e ben organizzati può sembrare in contrasto con il secondo principio della termodinamica secondo il quale un sistema si evolve sempre per aumentare l'entropia (disordine), ma questo principio si applica soltanto ai sistemi in equilibrio o vicini all'equilibrio. Sulla Terra l'energia è continuamente assorbita dal Sole e abbiamo un sistema aperto fuori dall'equilibrio. Il flusso d'energia attraverso un sistema può produrre ordine locale. L'adattamento all'ambiente richiama la naturale tendenza verso l'equilibrio ma, in questo caso, l'ambiente cambia continuamente.
L'origine della vita e l'evoluzione
Un organismo vivente si caratterizza come un sistema capace di metabolizzare, riprodursi ed evolversi. Non è semplice tradurre queste proprietà nel linguaggio della fisica, ma ciò che noi adesso chiamiamo complessità in un senso molto vago sembra avvicinarsi di più a questo concetto. La vita è comparsa sulla Terra sotto forma di batteri monocellulari circa 3,5 miliardi di anni fa, 300 milioni di anni dopo che la superficie della Terra si è solidificata. Non vi sono testimonianze dell' evoluzione prebiotica che portò alla struttura della prima cellula. Dopo moltissimo tempo, soltanto 800 milioni di anni fa, sono apparsi gli organismi multicellulari. In seguito, nel Cambriano (550 milioni di anni fa), si è verificata un'esplosione di forme di vita ed è apparso un gran numero di organismi diversi; poco dopo si sono sviluppati i primi vertebrati. I primi ominidi sono apparsi 3 milioni di anni fa.
Secondo l'idea originale di Charles Darwin, l'evoluzione si manifesta attraverso una selezione graduale di varianti utili. Vi sono pochi dubbi sul fatto che la selezione naturale sia l'ingrediente chiave per capire l'evoluzione. Comunque, questo concetto da solo sembra essere incompleto e i tentativi di definire il modo specifico in cui opera sono ancora piuttosto controversi. Per esempio, secondo Darwin ci potremmo aspettare una dinamica bottom up (dal basso in alto) che, a partire dagli organismi semplici, porti poi a quelli più complessi. I dati forniti dai fossili invece ci dimostrano che l'esplosione cambriana corrisponde piuttosto a una dinamica top down (dall'alto in basso). Le diverse strutture fondamentali (i phyla) comparvero in un periodo relativamente breve e, in seguito, da queste strutture basilari si sono sviluppate le classi, le famiglie, i generi e le specie.
La più grande estinzione conosciuta non è stata quella del Cretaceo, che 65 milioni di anni fa portò alla scomparsa dei dinosauri. Infatti nell'estinzione permiana, avvenuta 245 milioni di anni fa, scomparve il 96% di tutte le specie. Questo evento è stato seguito da una nuova ondata di evoluzione e diversificazione che procedette invece dal basso verso l'alto.
Dal punto di vista della fisica statistica moderna, l'evoluzione regolare implicata dalla più semplice 'implementazione' delle idee darwiniane appare come una approssimazione della vera dinamica che, data la complessità del sistema, è naturale che possa essere non analitica e fortemente irregolare. Inoltre, sono ancora oscuri i meccanismi dinamici con i quali il processo ha avuto inizio e rimane stabile. In altri termini, se consideriamo la vita e l'intero processo evolutivo come fenomeno altamente ordinato, uno dei problemi più importanti è di capire come questo stato di ordine abbia potuto emergere spontaneamente.
Autoorganizzazione, evoluzione e selezione naturale
Una domanda anche più basilare in connessione con l'idea di Darwin è come definire quali sistemi si possono evolvere attraverso una selezione naturale. Per esempio, se cambiamo in modo casuale un programma che fa certi calcoli, è altamente improbabile che otteniamo un programma migliore, anche se proviamo un'enorme quantità di volte. È facile rendersi conto che quasi tutti i sistemi che conosciamo non possono evolversi e migliorare attraverso la selezione naturale.
Un altro concetto della fisica statistica moderna dal quale possiamo trarre qualche ispirazione è la criticità autoorganizzata. Si potrebbe ipotizzare che l'idea della selezione darwiniana sia soltanto un elemento essenziale da inserire in uno schema più ampio di auto organizzazione verso lo stato critico corrispondente alla struttura quasi stabile della vita sulla Terra. In quest'ottica la complessità della cellula, già prima che l'evoluzione cominci ad avere un ruolo, può essere interpretata come originata da meccanismi di autoorganizzazione. Più tardi la dinamica del processo auto organizzato si arricchisce dell'enorme potenza del meccanismo dell'evoluzione e della selezione. Tutto il processo è auto-critico nel senso che mantiene il sistema in equilibrio tra ordine e caos (Kauffman, 1993).
Possiamo renderci conto immediatamente dell'importanza di questa nuova prospettiva tentando di stimare la probabilità dell'emergere della vita, argomento altamente discusso. Se infatti partiamo dal concetto che le prime entità viventi siano state generate più o meno casualmente, la probabilità che ciò possa accadere è incredibilmente piccola. Se invece adottiamo il punto di vista di un meccanismo auto organizzato, possiamo concludere che l'emergere della vita è molto più probabile o addirittura inevitabile in opportune condizioni.
Esperimenti: dati fossili
Dai dati fossili più recenti possiamo riassumere le seguenti indicazioni principali (Solé et al., 1997):
1. Le dimensioni delle estinzioni sono descritte approssimativamente da una distribuzione a legge di potenza. Questo significa che la probabilità P che, in un certo intervallo di tempo, n specie si estinguano è data da P = n-2.
2. Il numero di generi N con un tempo di sopravvivenza, è dato da N = τ-a, con a =2,1 e τmedio = 20 milioni di anni.
3. Lo spettro di potenza (scomposizione in armoniche) per la frequenza delle estinzioni e per il numero di specie e generi presenti in un dato periodo è ben rappresentato da un comportamento di tipo I/f, dove f è la frequenza; questa proprietà del rumore, cioè delle fluttuazioni temporali del valore di tali grandezze, corrisponde a una sorta di comportamento frattale nel tempo.
4. Tagliando l'albero filo genetico a diversi livelli di ramificazione si evidenzia una relazione a legge di potenza tra il numero di generi e il numero delle specie.
5. La frazione del numero totale di specie in un dato gruppo sembra decadere esponenzialmente col tempo. Si noti che le scale temporali caratteristiche di questi decadimenti esponenziali sono invece distribuite secondo una legge di potenza (punto 2). Come abbiamo discusso nel paragrafo sulle proprietà dei frattali, le distribuzioni a legge di potenza sono aspetti caratteristici delle proprietà di invarianza di scala (così vale anche per il rumore I/f). In realtà abbiamo una situazione mista di comportamento esponenziale con una distribuzione delle scale temporali a legge di potenza, una combinazione che incontriamo anche in alcuni problemi fisici. Sembra quindi naturale considerare la dinamica dell' evoluzione biologica come un problema estremamente difficile nel quale però la comprensione dello sviluppo spontaneo delle proprietà dell'invarianza di scala dovrebbe giocare un ruolo importante. Possiamo dunque ragionevolmente aspettarci che i concetti e i metodi sviluppati ne II ' ambito della fisica statistica possano fornire una nuova prospettiva in questo campo.
Adattamento in potenziali variabili (profili di fitness)
L'evoluzione adattativa consiste nell'accumulo progressivo di piccole variazioni del fenotipo. L'idea è che il genotipo venga sottoposto a fluttuazioni casuali a ogni generazione e che questo fatto modifichi la fitness (capacità di adattamento) del sistema rispetto all'ambiente. La fitness può essere definita grosso modo come la probabilità del sistema di sopravvivere e di generarsi. l fenotipi con la miglior fitness hanno una probabilità maggiore per la generazione futura. Questo porta a un processo di adattamento attraverso la selezione. È facile notare che già a livello di questo semplice esempio la situazione ottimale corrisponde a una combinazione opportuna di casualità e regolarità. La casualità è necessaria per produrre i cambiamenti nel genotipo e una certa regolarità è indispensabile per rendere la selezione efficace. Dal punto di vista dei modelli fisici, il processo della microevoluzione è relativamente facile da formulare. Per esempio, nella sua forma più semplice è simile alla ricerca delle configurazioni ottimali (minimi di energia) di un sistema sottoposto a date condizioni e interazioni. Questo porta a un profilo (landscape) di fitness (che in fisica corrisponde a una curva di potenziale), nel quale il sistema può muoversi (evoluzione) per raggiungere l'equilibrio migliore (un massimo di fitness).
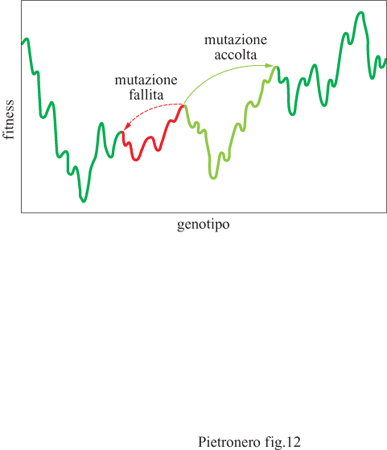
Il modello dell' adattamento in un potenziale fluttuante si è rivelato molto utile per l'analisi di alcuni possibili meccanismi evolutivi (Kauffinan, 1993). Definendo la fitness come una variabile matematica, per esempio come la probabilità di generare, si assume che a ogni genotipo corrisponda un certo valore di fitness che dipende dall'ambiente. Questa descrizione ha una relazione diretta con la meccanica statistica, in cui a ogni configurazione degli atomi corrisponde un certo valore dell' energia potenziale che porta a una curva del tipo rappresentato schematicamente in figura (fig. 12). In tal senso, è possibile utilizzare direttamente in questo contesto vari concetti e metodi della meccanica statistica.
S.A. Kauffman e collaboratori (Kaufmann, 1993) hanno considerato modelli di ottimizzazione (evoluzione) in un potenziale ispirati all'evoluzione delle proteine. In questo caso la fitness corrisponde alla capacità della proteina di catalizzare una reazione specifica. La maggior parte di questi studi si basa su un modello con due parametri, il modello NK. N rappresenta il numero di geni nel cromosoma e ogni gene può assumere due configurazioni, 0 oppure 1. La fitness di ogni gene dipende da se stesso e dai geni in altre K posizioni. Per ogni combinazione di K elementi viene assegnato un valore casuale per la fitness. L'idea è che queste configurazioni dipendano dall' ambiente in un modo così complesso che può essere considerato casuale. Il punto cruciale non è l'assegnazione di questi valori, ma come il sistema si ottimizza per una data assegnazione. Partendo da una configurazione iniziale dei geni si procede con mutazioni casuali che vengono accettate se la loro fitness finale è migliorata. Un elemento interessante di questo modello è che esso porta a potenziali il cui grado di irregolarità può essere controllato con i parametri del modello. Per piccoli valori di K il potenziale è piuttosto regolare con pochi massimi facilmente accessibili. Se il valore di K è invece grande, dell'ordine di N, il potenziale diventa fortemente irregolare con molti massimi (di fitness) locali e il sistema rimane intrappolato in un massimo locale dopo alcuni passi del processo evolutivo. Questa situazione ricorda molto il modello dei vetri di spino Questi studi sul modello NK hanno prodotto vari risultati interessanti, soprattutto in relazione alla microevoluzione. Un risultato generale è che l'evoluzione ottimale corrisponde a una combinazione opportuna di ordine e disordine: l'ordine per garantire una certa stabilità al processo evolutivo e il disordine per poter avere una certa variabilità e ricchezza nelle possibili mutazioni. D'altra parte, le limitazioni di questo modello sono date dal fatto che non possiede alcun elemento di auto organizzazione e che è eccessivamente statico. Una volta raggiunte le posizioni ottimali, il sistema smette di evolversi.
Microevoluzione, coevoluzione e macroevoluzione
Il concetto del profilo di fitness, che abbiamo appena discusso e sul quale torneremo anche in seguito, è forse il più vicino all'idea originale di DaIwin e ci porta a risultati interessanti, ma nello stesso tempo evidenzia alcuni limiti crociali. In questo modello l'evoluzione è troppo regolare e continua ed è difficile definire il fenomeno dell' apparizione delle nuove specie (speciazione) e di tutti quegli eventi fortemente irregolari che hanno portato al concetto di equilibrio puntuato (Gould, 1996).
La situazione descritta precedentemente si riferisce però al caso di una singola specie in un potenziale fisso. Il modello può essere generalizzato considerando esplicitamente le interazioni tra le diverse specie (coevoluzione). La forma più semplice di questo effetto è la relazione tra preda e predatore che porta alle famose equazioni di Volterra che costituiscono uno dei primi esempi di caos deterministico. Nell'evoluzione biologica si trovano certamente alcuni elementi caotici (Kauffman, 1993), però in un regime caotico le fluttuazioni e le correlazioni decadono esponenzialmente (esponenti di Lyapunov). In questo senso il comportamento di un sistema caotico appare troppo aleatorio rispetto alle proprietà critiche (leggi di potenza) osservate nella maggior parte dei dati. È facile immaginarsi quale livello di complessità possa essere raggiunto se si considerano molte specie che interagiscono in un ambiente che può anche cambiare nel tempo. Una visione diversa del problema della coevoluzione è rappresentata dal modello di P. Bak e K. Sneppen (1993). Questo modello è estremamente semplificato e non chiarisce la relazione tra microevoluzione e macroevoluzione, ma indica una situazione in cui la coevoluzione può portare spontaneamente (autoorganizzazione) a un equilibrio critico tra ordine e disordine.
Il concetto della macroevoluzione si riferisce al comportamento globale del processo evolutivo, l'apparire di nuove specie, la complessa ramificazione auto simile degli alberi filogenetici e la distribuzione degli eventi d'estinzione. In linea di principio, questi fenomeni dovrebbero essere connessi alla microevoluzione ma, al momento, questo appare come uno dei problemi aperti più complessi. Uno dei fatti più difficili da spiegare è perché le specie sono stabili per lunghi periodi di tempo, seguiti da eventi improvvisi, come lo sviluppo di nuove specie in tempi relativamente brevi; queste osservazioni hanno portato allo sviluppo del concetto di equilibrio puntuato (Gould, 1996). Questi aspetti di forte irregolarità coinvolgono anche i fenomeni di estinzione che, come abbiamo visto, sono caratterizzati da eventi a valanga di tutte le dimensioni.
Una possibilità è che questi eventi drastici potrebbero essere dovuti a qualche agente esterno come i meteoriti. La nostra conoscenza delle dinamiche dei sistemi complessi irreversibili ci suggerisce però anche la possibilità di ipotesi diverse. Abbiamo molte specie che interagiscono tra loro e agiscono in un ambiente complesso. Questo fatto ci fa pensare che potrebbe essere la dinamica del sistema stesso che porta spontaneamente a uno stato critico con proprietà irregolari caratterizzate da esplosioni evoluzionistiche e instabilità di ogni dimensione. Naturalmente queste ipotesi dovrebbero essere poi sviluppate con l'identificazione dei meccanismi specifici responsabili di queste proprietà e che possano essere confrontati, in linea di principio, con i dati sperimentali.
L'invasione di nuovi spazi delle fasi
Uno di questi meccanismi può essere l'invasione improvvisa di aree nuove e inaspettate dell' eco sistema. Per esempio, lo sviluppo delle ali e la successiva possibilità di volare rappresentano questo tipo di situazione, che è qualitativamente diversa dai concetti evoluzionistici elementari. La selezione funziona per i cambiamenti graduali e quindi lo sviluppo delle ali, che permettono di volare solo se superano una certa grandezza, deve essere stato motivato da qualche altro fattore. Sembra infatti che lo scopo originale fosse il raffreddamento del sangue. La selezione ha funzionato quindi come meccanismo di microevoluzione per questi radiatori di sangue che, presumibilmente, si sono sviluppati maggiormente nelle regioni a clima caldo. A un certo punto, le ali devono aver raggiunto una grandezza sufficiente per piccoli voli. In questo periodo i fenotipi che iniziano a volare sperimentano un profilo di fitness completamente diverso da prima. La possibilità di volare apre una quantità di nuove dinamiche per l'evoluzione che non hanno relazioni con la microevoluzione che ha generato l'organo del volo per motivi diversi. In questo senso, il fenomeno non è contenuto nel quadro tradizionale dell'evoluzione. Questo cambiamento drastico e imprevedibile porta a una rapida ottimizzazione rispetto alla nuova situazione che si riferisce a un diverso tipo di microevoluzione. Essendo queste ali primitive ben lontane dall'ottimizzazione, la nuova evoluzione procede molto rapidamente rispetto alla precedente. Si può quindi proporre questo fenomeno come un possibile meccanismo per una rapida speciazione preceduta da una lunga stasi. In termini fisici chiameremo questo evento una biforcazione o un punto di comportamento non analitico, che potrebbe rappresentare il punto di contatto tra la micro- e la macroevoluzione. Una delle questioni crociali è quanto spesso la bioevoluzione incontri casualmente questi punti nei quali lo spazio delle fasi delle possibilità evolutive si apre repentinamente verso nuove situazioni impreviste. Se, come sembra, questi fenomeni sono in realtà molto frequenti, si potrebbe ipotizzare una nuova prospettiva per la connessione tra la micro- e la macroevoluzione all'interno della fenomenologia dell'equilibrio puntuato (Pietronero, 1998). Le conseguenze più importanti di questo punto di vista sono che la stabilità di tutto il processo evolutivo è dovuta alla continua invasione di nuovi spazi. È ragionevole ipotizzare che questo accada maggiormente prima che gli organi che sono in fase di sviluppo raggiungano i loro requisiti ottimali. Un'eccessiva ottimizzazione rende quindi il sistema statico rispetto a questi bruschi cambiamenti. La stabilità globale viene raggiunta dai cambiamenti continui (instabilità) a livello locale. Il sistema deve essere in grado di invadere continuamente nuovi spazi, in modo da rimanere globalmente stabile. Queste idee sono al momento del tutto speculative, ma suggeriscono un percorso interessante per sviluppi futuri.
La vita come stato di criticità autoorganizzato tra ordine e caos
Riassumendo, possiamo aspettarci che la fisica dei sistemi invarianti di scala e auto organizzati possa essere rilevante per l'evoluzione biologica nei punti seguenti:
1. Autoorganizzazione delle prime strutture, come le cellule; questo dovrebbe accadere prima che l'evoluzione cominci ad avere un ruolo.
2. Inserimento della selezione naturale all'interno di uno schema più ampio di auto organizzazione e definizione di leggi generali per l'emergenza di queste proprietà. Le dinamiche irreversibili del processo trasformano l'insorgere della vita in un processo dipendente specificamente dalla sua particolare storia. La possibilità di storie alternative può essere considerata in una nuova prospettiva. Nella visione tradizionale la vita appare come una sorta di evento accidentale con probabilità estremamente basse. Il quadro della auto organizzazione, non ancora ben definito operativamente, potrebbe aumentare di molto queste probabilità e rendere l'apparire della vita più naturale, se non addirittura inevitabile in opportune condizioni.
3. Identificazione di sistemi e ambienti che possono condurre a un processo efficace di evoluzione attraverso la selezione. Vi sono indicazioni che un meccanismo di autoorganizzazione e di evoluzione dovrebbe mantenere il sistema in uno stato critico tra ordine e caos.
4. Comprensione dell'origine della natura discontinua dell'evoluzione. Ramificazioni o estinzioni improvvise sono precedute e seguite da lunghi periodi di relativa stabilità (equilibrio puntuato). Queste dinamiche altamente irregolari appaiono legate in modo naturale al comportamento a legge di potenza di molti dati fossili. Le dimensioni e i tempi delle estinzioni si estendono su ampie distribuzioni di valori con proprietà di invarianza di scala. Sotto questa prospettiva sembra importante studiare le leggi generali per il comportamento dei processi di selezione e auto organizzazione.
Questo programma è molto speculativo e finora sono stati fatti soltanto passi molto limitati. È possibile progredire selezionando alcuni punti specifici, sviluppando li in dettaglio e confrontando li con i dati a disposizione. In ogni caso i concetti descritti danno un'idea di come i recenti progressi sulle strutture invarianti di scala in fisica possano avere un impatto nella biologia, fornendo una nuova prospettiva all'affascinante problema dell' emergere e dello stabilizzarsi di strutture ordinate.
L'invarianza di scala in fisiologia
La fisiologia è un campo in cui l'invarianza di scala e le strutture frattali sono molto frequenti. Uno dei motivi è che gli scambi con l'ambiente avvengono su superfici che devono essere molto estese ma anche inserite in un corpo compatto. Questo requisito porta naturalmente alle strutture frattali e auto simili. Un esempio comune è il fatto che se ci pungiamo in un punto qualsiasi del nostro corpo uscirà del sangue. Dal punto di vista geometrico questo dovrebbe apparire strano perché il volume totale del nostro sangue è meno del 10% del volume del corpo. Ciò implica che la distribuzione dei vasi sanguigni non può essere semplicemente euclidea e che le superfici devono essere estremamente estese. Questa è proprio una caratteristica dei frattali i quali, in sostanza, sono quasi interamente composti di superficie. Un esempio è rappresentato dalla struttura dei vasi sanguigni della retina umana. Altri esempi sono offerti dalla struttura dei reni e da quella dei polmoni. La superficie degli alveoli, nei quali ossigeno e diossido di carbonio vengono scambiati con l'ambiente, è dell'ordine di un chilometro quadrato. La struttura dell'albero bronchiale è stata analizzata recentemente usando concetti frattali e questo appare essere il quadro naturale per descrivere le loro proprietà (Havlin et al., 1995).
Altri sistemi biologici nei quali sono state identificate chiaramente strutture frattali sono le colonie batteri che mostrate in figura 2. In questi casi abbiamo una completa analogia con il modello DLA discusso in precedenza e addirittura i dettagli quantitativi sono ben riprodotti da questo modello. Più speculativa è l'ipotesi che la struttura del neurone, come mostra la figura (fig. 15), potrebbe essere frattale. Anche in questo caso il modello base sarebbe la DLA, con dimensioni frattali maggiori per i neuroni più sviluppati.
Il sorprendente esponente 1/4
Le dimensioni degli organismi viventi, dai microbi alle balene più grandi, si estendono su scale che possono variare di ben 21 ordini di grandezza. Questa osservazione già di per sé costituisce una notevole evidenza per qualche tipo di invarianza di scala. La dimensione condiziona le proprietà di tutte le strutture e funzioni biologiche e le relazioni tra il volume del corpo e la fisiologia sono state studiate in dettaglio con risultati sorprendenti (West et al., 1997). La relazione tra una variabile biologica Y e la dimensione del corpo M è normalmente caratterizzata dalla legge di potenza del tipo Y = YoMb. Se si ritenesse che queste leggi riflettano solo i vincoli geometrici imposti dalle dimensioni del corpo, ci si aspetterebbe che questi esponenti dipendano da una lunghezza caratteristica data dalla radice cubica della massa M. Ciò implicherebbe che l'esponente b sia un multiplo di 1/3. Invece si osserva che per il tasso metabolico di un organismo si ha b = 3/4. Il tasso metabolico delle cellule, il battito cardiaco e la crescita massima della popolazione presentano b =1/4. I tempi della circolazione sanguigna, la crescita embrionale e la durata della vita mostrano anch'essi b =1/4. Questi dati sono abbastanza generali e suggeriscono fortemente una struttura universale autosimile connessa all'esponente anomalo b=1/4, piuttosto che all'esponente 'euclideo' b=1/3. Tutto questo costituisce una chiara indicazione di proprietà frattali basate sugli stessi principi generali. Ispirati da queste considerazioni, G.B. West e collaboratori (1997) hanno sviluppato recentemente un modello per la rete che trasporta risorse in un organismo, basato sulla geometria e sulla idrodinamica frattali e caratterizzato da tre elementi essenziali: la rete riempie lo spazio, nel senso che deve raggiungere tutte le zone del corpo tridimensionale; l'energia dissipata per trasportare il materiale nel mezzo fluido deve essere minimizzata; i rami terminali (capillari) della rete devono avere la stessa dimensione minima. Il risultato è che la legge di potenza 1/4 appare naturalmente in questo modello che genera strutture frattali, come mostrato in figura (fig. 16).
Nonostante la natura altamente semplificata del modello, è quindi concepibile che questo possa essere il punto di partenza per studi più realistici basati su nuovi concetti e metodi ispirati alla fisica statistica. A questo riguardo l'invarianza di scala e la geometria frattale sembrano rappresentare uno degli argomenti più generali che sono alla base di tutte le diversità biologiche.
Bibliografia citata
AMIT, D.l. (1978) Field theory, the renormalization group and criticaI phenomena. Londra, McGraw-Hill.
BAK, P., SNEPPEN, K. (1993) Punctuated equilibrium and criticality in a sandpile model of evolution. Phys. Rev. Lett., 71, 4083-4086.
BAK, P., TANG, C., WIESENFELD, K. (1987) Self-organized criticality: an explaination of lifnoise. Phys. Rev. Lett., 59, 381-384.
COLEMAN, P.H., PIETRONERO, L. (1992) The fractal structure of the Universe. Phys. Rep., 213, 311-389.
ERZAN, A., PIETRONERO, L., VESPIGNANI, A. (1995) The fixed scale transformation approach to fractal growth. Rev. Mod. Phys., 67, 545-604.
EVERTSZ, C.lG., PEITGEN, H.O., Voss, R.F., a c. di (1996) Fractal geometry and analysis. Singapore, World Scientific.
GELL-MANN, M. (1994) The quark and the jaguar: adventures in the simple and the complex. New York, Freeman.
GOULD, S.I. (1996) Dynosaur in a haystack. Londra, Random House.
HAVLIN, S., BULDYREV, S.V., GOLDBERGER, A.L., MANTEGNA, R.N., OSSADNIK, S.M., PENG, C.-K., SIMONS, M., STANLEY, H.E. (1995) Fractals in biology and medicine. Chaos, Solitons and Fractals, 6, 171.
CADANOFF, L.P. (1990) Scaling and universality in statistical physics. Physica A, 163, 1-14.
CADANOFF, L.P. (1991) Complex structures from simple systems. Physics Today, 44, 9-11.
CAUFFMAN, S.A. (1993) The origins of order: selforganization and selection in evolution. New York, Oxford University Press.
MANDELBROT, B. (1983) The fractal geometry of nature. New York, Freeman.
MEZARD, M., PARISI, G., VIRASORO, M. (1987) Spin glass theory and beyond. Singapore, World Scientific.
NIEMEYER, L., PIETRONERO, L., WIESMANN, H.I. (1984) Fractal dimension of dielectric breakdoWI1. Phys. Rev. Lett., 52, 1033-1036.
PEEBLES, P.E.I. (1980) The large-scale structure of the Universe. Princeton, Princeton University Press.
PEEBLES, P.E.I. (1993) Principles of physical cosmology. Princeton, Princeton University Press.
PIETRONERO, L. (1998) A statistical model of exaptation. In corso di stampa.
PIETRONERO, L., MONTUORI, M., SYLOS LABINI, F. (1997) On the fractal structure in the visible Universe. In CriticaI dialogues in cosmology, a C. di Turok N. et al., Singapore, World Scientific, pp. 24-49.
PIETRONERO, L., TOSATTI, E. (1986) Fractals in physics. Amsterdam-New York, North Holland.
PIETRONERO, L., VESPIGNANI, A., ZAPPERI, S. (1994) Renormalization scheme for self-organized criticality in sandpile models. Phys. Rev. Lett., 72, 1690-1693.
SOLÉ R.V., MANRUBIA, S.C., BENTON, M., BAK, P. (1997) Selfsimilarity of extinction statistics in the fossil record. Nature, 388,764-767.
SYLOS LABINI, F., MONTUORI, M., PIETRONERO, L. (1998) Scale-invariance of galaxy clustering. Physics Reports, 293, 61-226.
VICSEK, T. (1992) Fractal growth phenomena. Singapore, World Scientific.
WEINBERG, S.E. (1972) Gravitation and cosmology. New York, Wiley.
WEITZ, D., OLIVERIA, M. (1984) Fractal structures formed by kinetic aggregation of aqueous gold colloids. Phys. Rev. Lett., 52, 1433-1436.
WEST, G.B., BROWN, I.H., ENQUlST, B.l (1997) A generaI model for the origin of allometric scaling laws in biology. Science, 276, 122-126.
WILSON, K.G. (1983) The renormalization group and criticaI phenomena. Rev. Mod. Phys., 55, 583-600.
WITTEN, T.A., SANDER, L.M. (1981) Diffusion-limited aggregation, a kinetic criticaI phenomenon. Phys. Rev. Lett., 47, 1400-1403
© Istituto della Enciclopedia Italiana - Riproduzione riservata