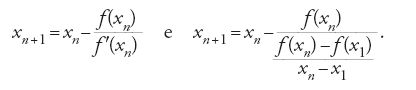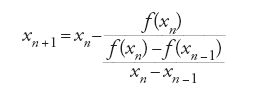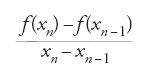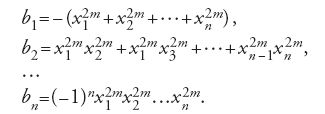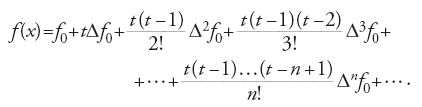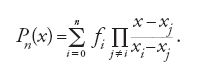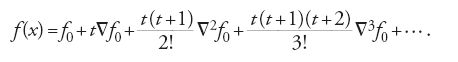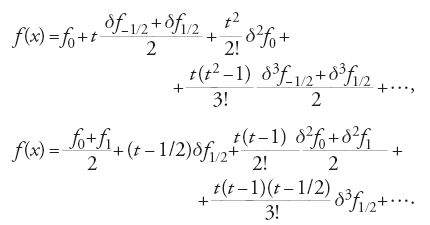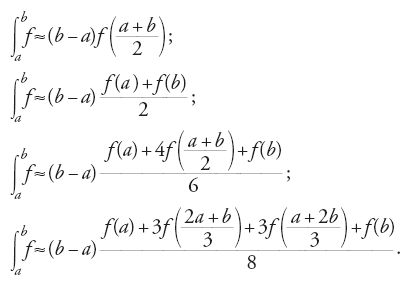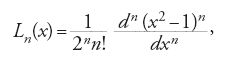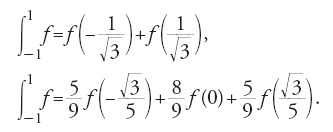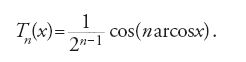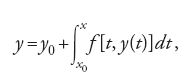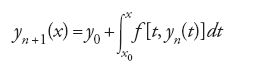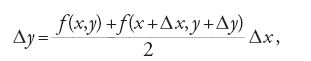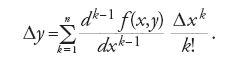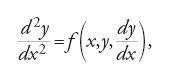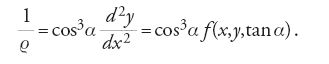L'Ottocento: matematica. Metodi del calcolo numerico

L'Ottocento: matematica. Metodi del calcolo numerico

Metodi del calcolo numerico

Prima del 1870 l'analisi numerica non si era ancora sviluppata come disciplina autonoma; esisteva naturalmente la necessità di effettuare calcoli, sia nella contabilità legata allo sviluppo delle attività finanziarie e commerciali, sia nei campi dell'ingegneria civile e militare, della fisica e dell'astronomia nei quali dovevano essere effettuate quotidianamente operazioni matematiche sempre più elaborate. Tuttavia le ricerche teoriche e pratiche necessarie per concepire, ottimizzare ed eseguire tali calcoli non erano organizzate, salvo eccezioni, attorno a pubblicazioni specifiche o a insegnamenti specializzati. Il più delle volte nuovi metodi di calcolo comparivano direttamente nelle applicazioni, a seconda delle esigenze, in luoghi e contesti diversi, salvo poi essere dimenticati e reinventati più volte in modo indipendente.

Pur tenendo presente questa situazione, è possibile tuttavia raggruppare sotto il termine generico di 'calcolo numerico' tutti i metodi, le tecniche e gli strumenti che servono a calcolare i valori numerici, nella maggior parte dei casi approssimati, di grandezze necessarie a coloro che si servono della matematica: soluzioni di equazioni algebriche o trascendenti, integrali definiti, valori particolari di funzioni determinate mediante un algoritmo algebrico finito o infinito, ottenuti interpolando a partire da una tavola di valori sperimentali, o implicitamente da un'equazione funzionale, differenziale o integrale. In tutto questo la principale innovazione del periodo 1800-1870 rispetto ai secoli precedenti è forse il fatto che sotto l'influenza di matematici come Joseph-Louis Lagrange, Jean-Baptiste-Joseph Fourier o Augustin-Louis Cauchy si sviluppi un interesse più esplicito verso concetti come la convergenza, la rapidità di convergenza e la valutazione dell'errore. In compenso non c'è ancora traccia, se non qua e là e allo stato embrionale, di altri argomenti essenziali nell'analisi numerica moderna, quali l'efficienza e la complessità degli algoritmi, la propagazione degli errori e la stabilità numerica.

Gli strumenti del calcolo numerico

Fin dal XVII sec. le tavole dei logaritmi sono state uno strumento prezioso per trasformare la moltiplicazione in addizione ed eliminare così la parte più faticosa del calcolo. Ai primi del XIX sec. l'esigenza di una sempre maggior precisione nei calcoli, in particolare in quelli astronomici, spinge a compilarne di nuove, con un numero molto maggiore di decimali. Ricordiamo le tavole a 10 decimali di Georg von Vega (1794), a 12 e 19 decimali di Gaspard-François-Clair-Marie Riche de Prony (1794) e a 28 decimali di Edward Sang (1848-1890). Si pubblicano anche nuove tavole delle funzioni trigonometriche e dei loro logaritmi, soprattutto in seguito all'adozione del grado come unità di misura dell'angolo stabilita dalla Rivoluzione francese.

La prima metà del XIX sec. è anche l'epoca in cui numerose applicazioni richiedono l'introduzione, accanto alle funzioni trigonometriche e logaritmiche, di nuove funzioni trascendenti chiamate 'funzioni speciali': integrali ellittici, funzioni ellittiche, funzioni Gamma e Beta, funzioni di Legendre, funzioni di Bessel, funzioni ipergeometriche, funzioni di Lamé e di Mathieu, ecc. Man mano che queste funzioni vengono fatte proprie dagli scienziati nel loro lavoro quotidiano, diviene indispensabile tabularle. Si stima che nel periodo 1800-1870 siano state compilate un migliaio di tavole matematiche, dato che dà una misura del fenomeno. Le prime tavole importanti di funzioni speciali sono quelle di Adrien-Marie Legendre (1752-1833) per la funzione Gamma e gli integrali ellittici, quelle di Christian Kramp (1799) e di Friedrich Wilhelm Bessel (1818) per la funzione degli errori, necessarie per l'applicazione della distribuzione normale di Gauss nel calcolo delle probabilità, e quelle di Bessel (1826) per le funzioni di Bessel J₀ e J₁.

Accanto alle tavole, un'altra famiglia di strumenti utili è quella delle macchine meccaniche che eseguono le operazioni aritmetiche elementari: addizione e sottrazione per le macchine più semplici, moltiplicazione e divisione per le più elaborate. Le prime, come quelle di Wilhelm Schickard (1623), Blaise Pascal (1642) o Gottfried Wilhelm Leibniz (1674), erano state costruite in alcune decine di esemplari riservati a pochi fruitori privilegiati. Ai primi del XIX sec. i progressi della tecnologia si uniscono alle esigenze di calcolo aritmetico dovute allo sviluppo delle transazioni contabili, nelle quali si addizionano continuamente lunghe colonne di cifre. Compariranno così nuove macchine, fabbricate in serie e suscettibili di una più ampia utilizzazione. Una delle più significative è l''aritmometro' di Charles-Xavier Thomas (1820), del quale furono venduti 1500 esemplari tra il 1821 e il 1878. Viene inventata a Colmar, in Alsazia, la prima macchina moltiplicatrice robusta, di tipo industriale, capace di fornire un servizio continuo e prolungato. Ispirata a quella di Leibniz, essa esegue ancora le moltiplicazioni sommando ripetutamente gli addendi. Le prime macchine a moltiplicazione diretta, che memorizzano una tavola pitagorica sotto forma di rappresentazione materiale, compariranno soltanto dopo il 1870.

In questo periodo, assistiamo anche ai primi sforzi volti a concepire strumenti meccanici che vadano al di là delle operazioni elementari. In Inghilterra Charles Babbage, spinto dai numerosi errori che scopre nelle tavole matematiche e nautiche dell'epoca, cerca di automatizzarne la costruzione. Intorno al 1820 egli concepisce l'idea di una 'macchina alle differenze', che avrebbe dovuto calcolare tavole numeriche con il metodo delle differenze finite e stampare automaticamente i risultati. A partire dal 1834 progetta una macchina ancora più ambiziosa, la 'macchina analitica', che può essere programmata grazie a schede perforate ispirate ai telai Jacquard per la tessitura e che prefigura i calcolatori moderni. Mancano, tuttavia, i finanziamenti e gli appoggi necessari e Babbage morirà nel 1871 senza essere riuscito a portare a compimento la costruzione della sua macchina. In compenso un ricco svedese, Georg Scheutz, ispirandosi ai lavori di Babbage, costruisce due macchine alle differenze che eseguono calcoli con numeri a 15 cifre mediante differenze quarte. La prima, completata nel 1853, fu venduta negli Stati Uniti, dove fu usata per il calcolo delle effemeridi, in particolare per la determinazione dell'orbita del pianeta Marte; la seconda, costruita nel 1859, fu utilizzata dal governo inglese per la compilazione di più di 600 tavole di matematica finanziaria.

Parallelamente al calcolo numerico propriamente detto, nel XIX sec. si faceva di frequente ricorso al calcolo grafico. In tale tipo di calcolo i numeri sono rappresentati, su un foglio da disegno, da segmenti di diversa lunghezza e le operazioni algebriche sui numeri sono sostituite da costruzioni geometriche su questi segmenti. Le costruzioni si possono fare con la riga, il compasso e altri strumenti da disegno di ogni tipo. Il calcolo grafico era particolarmente apprezzato dagli ingegneri in quanto, senza richiedere una grande precisione, risultava più rapido e meno faticoso del calcolo manuale o con le tavole dei logaritmi. Uno dei primi trattati di calcolo grafico appare nel 1839 a opera di Barthélemy-Édouard Cousinéry, ingegnere francese del genio civile.

Per analogia con le tavole numeriche si immaginarono, per il calcolo grafico, tavole grafiche formate da linee di livello, con scale graduate, mobili o meno, sulle quali si poteva leggere direttamente, in funzione dei dati, la soluzione di un'equazione o il valore di una funzione. Queste tavole grafiche, chiamate dapprima 'abachi', saranno denominate 'nomogrammi' alla fine del XIX secolo. I primi abachi furono costruiti nel 1795 da un fabbricante di Rouen, Louis-Ezéchiel Pouchet, per facilitare ‒ in particolare a commercianti e artigiani ‒ i calcoli aritmetici elementari e le conversioni di unità di misura conseguenti all'adozione delle nuove scale metriche di pesi e misure imposte dalla Rivoluzione francese. Nel 1843 Léon-Louis Lalanne, anch'egli ingegnere francese del genio civile, fece compiere alla teoria degli abachi un passo decisivo: utilizzando scale non regolari e sostituendo le variabili primitive con funzioni ausiliarie di queste, riuscì a ridurre le curve dell'abaco a delle rette: da qui una grande facilità di costruzione e di utilizzazione. Gli abachi di Lalanne, grazie al basso costo e alla loro praticità, furono immediatamente adottati dall'amministrazione francese per il calcolo dei materiali di sterro e di riporto richiesto dalla costruzione di una rete ferroviaria estesa all'intero territorio.

Nel 1846 Lalanne progettò un abaco, o 'contatore universale', fondato sull'uso di scale logaritmiche che permettesse di eseguire tutte le operazioni matematiche usuali. Questo mezzo, semplice e a buon mercato, non ottenne il successo sperato, avendo subito la concorrenza del regolo calcolatore, altro equivalente grafico delle tavole dei logaritmi inventato dagli Inglesi nel XVII secolo. L'uso del regolo calcolatore si diffuse nel Continente intorno alla metà del XIX sec., soprattutto in seguito a un miglioramento decisivo introdotto da un ufficiale di artiglieria francese, Amédée Mannheim; questi nel 1850 suggerì di aggiungere un cursore trasparente a doppia faccia, permettendo in tal modo di riportare automaticamente i risultati di una scala su un'altra e di concatenare facilmente più operazioni. Grazie a questa innovazione il regolo calcolatore raggiunse una forma pressappoco definitiva e divenne rapidamente lo strumento prediletto di fisici e ingegneri.

Un'ultima famiglia di strumenti è quella degli strumenti grafici per l'integrazione meccanica, che compaiono nella prima metà del XIX sec. per facilitare le operazioni di calcolo infinitesimale. Planimetri (apparecchi che misurano l'area della superficie limitata da un contorno chiuso), integrometri (per misurare il valore dell'integrale di una funzione data graficamente), integrafi (che tracciano direttamente la curva che rappresenta l'integrale), sono strumenti concepiti attorno a una 'rotella integrante' solidale a un indice, che segue il contorno della superficie e il cui angolo di rotazione è proporzionale alla sua area. Sembra che il primo a costruire un tale apparecchio sia stato l'ingegnere bavarese Johann Martin Hermann nel 1814, utilizzando una rotella fatta ruotare su una superficie conica. Dopo Hermann altri ingegneri pensarono di far ruotare la rotella integrante su un disco, poi direttamente sul piano del foglio, fino a giungere al famoso planimetro polare ideato nel 1854 da Jacob Amsler, allora studente universitario a Königsberg. Questo planimetro, semplice e relativamente poco costoso, ebbe un grande successo commerciale: si stima che ne siano stati costruiti, in diverse varianti, più di 500.000 esemplari.

Equazioni numeriche

Uno dei problemi più comuni del calcolo numerico è la risoluzione approssimata delle equazioni algebriche o trascendenti. Prima del 1800 erano stati messi a punto numerosi metodi di calcolo per approssimazioni successive delle soluzioni di queste equazioni. Tali metodi iterativi, eredi dei metodi della falsa posizione, delle tecniche di interpolazione degli astronomi e degli algoritmi per l'estrazione di radici quadrate o cubiche, si basano il più delle volte su due grandi idee: la linearizzazione mediante il calcolo differenziale che va sotto il nome di 'metodo di Newton-Raphson' o 'metodo delle tangenti', e l'interpolazione lineare. Per un'equazione f(x)=0 questi metodi si traducono rispettivamente negli schemi di correzioni successive:

In altri termini, a ogni passo il valore precedente viene corretto con un procedimento che geometricamente significa sostituire la curva che rappresenta la funzione f con una tangente o una corda. Si trova anche, a volte, lo schema intermedio doppiamente ricorrente:

che può essere visto sia come un miglioramento del metodo di interpolazione lineare (perché prende in considerazione i due valori approssimati precedenti) sia come un adattamento pratico del metodo di Newton-Raphson nel quale la derivata f′(x_n), spesso difficile da calcolare, viene sostituita dal tasso di variazione

che l'approssima abbastanza bene quando i valori x_n e x_n−1 sono molto vicini. Infine, soprattutto fra gli astronomi e nel caso di equazioni trascendenti (frequenti in astronomia per via dell'onnipresenza delle funzioni trigonometriche), si trovano regolarmente schemi di approssimazioni successive più generali del tipo x_n+1=φ(x_n), dove la funzione φ viene scelta opportunamente (cioè in modo da assicurare empiricamente la convergenza).

All'inizio del XIX sec. comincia una riflessione teorica su questi metodi. Nel 1826 Germinal-Pierre Dandelin (1794-1847), basandosi sul fatto che il grafico di una funzione convessa è situato sotto le proprie corde e sopra le sue tangenti, osserva che, se si utilizzano congiuntamente il metodo di interpolazione e quello di Newton-Raphson, si ottiene un intervallo di valori che contiene la radice cercata, e quindi una valutazione dell'errore. Si assiste inoltre a uno studio approfondito del metodo di Newton-Raphson, di gran lunga il metodo preferito per via del buon compromesso che offre tra rapidità di convergenza e facilità di applicazione. Lagrange (1798) determina le condizioni iniziali che ne assicurano la convergenza, Fourier (1818) ne misura la rapidità di convergenza, raddoppiando a ogni passo il numero di cifre decimali esatte, e Cauchy (1821) ne calcola i limiti precisi di errore. Egli studia anche la convergenza del metodo generale delle approssimazioni successive.

Riguardo alle equazioni polinomiali Paolo Ruffini (1804), François-Desiré Budan (1807), William Horner (1819) e Teofilo Holdred (1820) pubblicano, indipendentemente l'uno dall'altro, varianti di quello che oggi si chiama lo 'schema di Horner'. Questo schema, del quale peraltro sono note numerose anticipazioni anteriori al XIX sec., è un algoritmo che ottimizza il calcolo dei coefficienti del polinomio P(x+α) a partire da quelli del polinomio P(x), facilitando l'estrazione progressiva delle cifre di una radice di P(x) per mezzo di trasformazioni successive dell'equazione P(x)=0 e restituendo così interesse a metodi antichi che erano stati abbandonati per la complessità dei calcoli. L'idea è quella di mettere un'espressione polinomiale:

[4]  a_nx_n+a_n-1x^n-1+…+a₁x+a0

nella forma

[5]  (…((a_nx+a_n-1)x+a_n-2)x+…+a₁)x+a₀

allo scopo di minimizzare il numero delle moltiplicazioni da effettuare.

Per calcolare le radici di un polinomio Dandelin (1826), Nikolaj Ivanovič Lobačevskij (1834) e Karl Heinrich Graeffe (1837) seguirono, indipendentemente l'uno dall'altro, un'altra via, più marginale ma con sviluppi che arriveranno fino ai nostri giorni. Si moltiplica il polinomio

[6] P(x)=(x-x₁)(x-x₂)…(x-x_n)

per P(−x) e si ottiene

Ripetendo questo procedimento m volte si arriva a un'equazione:

[8]  (x^2m)ⁿ+b₁(x^2m)^n-1+…+b_n=0.

Si ha allora:

Consideriamo per semplicità il caso in cui le radici sono reali, positive e distinte (negli altri casi occorre fare delle modifiche), numerate dalla più grande alla più piccola. Con l'elevazione alla potenza 2m le radici si separano notevolmente e ciò permette di ottenere in una sola volta delle buone approssimazioni per tutte le radici:

Infine, sempre nel caso delle equazioni polinomiali, occorre sottolineare il ruolo dei metodi grafici. Per le equazioni più comuni di grado non elevato, si fa progressivamente ricorso ad abachi: uno dei primi è quello di Lalanne, del 1846, per le equazioni di terzo grado. Più in generale si sviluppano tecniche di calcolo grafico per costruire per punti la curva di equazione P(x)=0 e leggere sul grafico i valori numerici delle radici. Nelle Leçons à l'École Normale de l'an III (1795) Lagrange pubblica una costruzione inventata nel secolo precedente da Johann Andreas von Segner. Un'altra tecnica, detta 'metodo dell'ortogono di Lill', viene pubblicata nel 1867 da Eduard Lill, un oscuro capitano del Genio dell'esercito austriaco. La costruzione di Segner si basa sul tracciato di rette parallele, quella di Lill sul tracciato di rette perpendicolari, ma in entrambi i casi si tratta di equivalenti grafici dello schema di Horner che minimizzano il numero di costruzioni geometriche elementari da effettuare.

Sistemi di equazioni lineari

Ai primi del XIX sec. nei lavori di astronomia e di geodesia intervengono sistemi lineari con un gran numero di equazioni. Inoltre, le misure sperimentali sono in pratica più numerose delle quantità indeterminate. Per esempio, bastano tre osservazioni per determinare l'orbita di una cometa, ma in generale se ne fanno molte di più nella speranza di migliorare la precisione e ciò conduce, tenuto conto degli errori di misura, a un sistema incompatibile, con più equazioni che incognite. Per trattare in modo ottimale un tale sistema Legendre (1805) e Carl Friedrich Gauss (1809) mettono a punto il 'metodo dei minimi quadrati'. Dato un sistema di k equazioni a n incognite (con k>n), in forma matriciale MX+N=0, si cerca il valore di X che minimizza ∥MX+N∥² per la struttura euclidea, cioè la somma dei quadrati degli errori. Questo valore di X è ottenuto come soluzione del sistema ^tMMX+^tMN=0 di n equazioni a n incognite, detto 'sistema delle equazioni normali'. Nel periodo che qui ci interessa, un problema essenziale del calcolo numerico è dunque la risoluzione efficiente di grandi sistemi AX=B con un numero di equazioni pari al numero delle incognite. Le formule di Gabriel Cramer (1750), che forniscono il valore delle incognite sotto forma di un quoziente di due determinanti, non sono utilizzabili in questo contesto perché il numero di operazioni aritmetiche da eseguire diventa proibitivo al di là di tre o quattro equazioni. Era dunque assolutamente necessario definire nuovi algoritmi.

In una memoria del 1810 riguardante l'orbita dell'asteroide Pallade, Gauss pubblica il procedimento di eliminazione noto oggi come 'metodo del pivot'. L'idea generale alla base di tale algoritmo è di arrivare progressivamente a ottenere un sistema triangolare, sapendo che un tale sistema si risolve facilmente a partire dall'ultima equazione. Si tratta, per grandi linee, di scegliere a ogni passo un coefficiente non nullo (il pivot) su una delle colonne della matrice e, dopo aver eventualmente permutato le righe per portare questo pivot sulla diagonale principale, far apparire degli zeri al di sotto mediante opportune combinazioni lineari delle righe. Ciò equivale a trovare una matrice invertibile M tale che la matrice prodotto MA sia triangolare superiore, e a risolvere il sistema nella forma MAX=MB. Ci si rende pienamente conto dell'efficienza di questo algoritmo, osservando che il numero di operazioni aritmetiche da effettuare con il metodo di Gauss è dell'ordine di 2n³/3, mentre con il metodo di Cramer è dell'ordine di n²n! (per n=6, caso frequente in astronomia, occorrono 144 operazioni nel primo caso e circa 26.000 nel secondo).

Dopo il 1817 Gauss si allontana dall'astronomia per approfondire maggiormente gli studi sulla geodesia. Incaricato di svolgere un programma di triangolazione del ducato di Hannover utilizzando una catena di 26 triangoli, egli si trova davanti a sistemi di equazioni enormi per i quali lo stesso metodo del pivot diventa impraticabile. In una lettera indirizzata a Christian Ludwig Gerling del 1823 Gauss propone un metodo iterativo per accelerare i calcoli. Sia A=D−E−F, dove D è la matrice diagonale avente gli stessi elementi diagonali di A e −E (rispettivamente −F) è la matrice avente gli stessi elementi di A al di sotto (rispettivamente al di sopra) della diagonale principale e zero altrove. Il sistema si può scrivere allora nel modo seguente: (D−E)X=FX+B. Senza entrare nei dettagli, Gauss determina un primo valore approssimato X₀ e poi lo corregge mediante le formule:

[11]  X_n+1=(D-E)^-1FX_n+(D-E)^-1B

finché non vi è più una sensibile differenza tra due valori successivi. Lo stesso algoritmo sarà riscoperto in maniera indipendente da Ludwig Seidel nel 1874, un astronomo che doveva risolvere un sistema di 72 equazioni per lo studio della luminosità delle stelle: da qui il nome oggi in uso di 'metodo di Gauss-Seidel'.

Carl Gustav Jacob Jacobi (1804-1851), anch'egli alle prese con grandi sistemi lineari originati da problemi di meccanica celeste o dallo studio di sistemi fisici sottoposti a piccole oscillazioni, pubblica nel 1845 un algoritmo dello stesso tipo di quello di Gauss-Seidel. Particolarmente adatto al caso in cui i coefficienti diagonali sono preponderanti, esso si scrive:

[12]  X_n+1=D^-1(E+F)X_n+D^-1B.

Sia nel metodo di Jacobi sia in quello di Gauss-Seidel l'idea è quella di mettere il sistema nella forma X=UX+V, dove U è una matrice tale che ∥U∥⟨1 per assicurare la convergenza. Gauss e Jacobi non affrontano esplicitamente questo problema teorico e per la scelta di una matrice V opportuna si rimettono all'abilità di chi effettua i calcoli. Seidel invece dimostra esplicitamente la convergenza, almeno nel quadro dei problemi che gli interessano.

Differenze finite, interpolazione di funzioni, quadrature numeriche

Un fisico o un ingegnere conoscono spesso una funzione soltanto in un numero finito di valori ottenuti sperimentalmente; a partire da questi devono interpolare i valori mancanti. D'altra parte, per la compilazione di tavole numeriche si calcolano direttamente e con grande precisione un certo numero di valori di partenza, ottenendo poi gli altri valori per interpolazione a partire dai primi. È lo stesso lavoro che deve compiere chi utilizza le tavole quando ha bisogno di valori diversi da quelli tabulati. Tutto ciò mostra il ruolo centrale che gioca l'interpolazione nelle applicazioni della matematica e nel calcolo numerico.

Dopo i lavori di Newton e della scuola inglese dei primi del XVIII sec., l'interpolazione si basa sulle differenze finite. Si consideri una funzione f della quale si conoscono i valori f_i=f(x_i) in punti equidistanti x_i = x₀+ih, con i intero positivo o negativo (nel seguito per semplificare ci limiteremo al caso di valori equidistanti, ma esistono anche formule per il caso generale). Come calcolare f(x) per un valore x=x₀+th che non si trova nella tavola? In pratica, il metodo usuale consiste nell'introdurre le 'differenze finite progressive', definite da Δf_i=f_i+1−f_i e, per m≥2, da Δ^mf_i=Δ^m−1f_i+1−Δ^m−1f_i, e nell'utilizzare la 'formula d'interpolazione progressiva di Gregory-Newton':

Troncando questa serie all'ordine n si ottiene un'approssimazione della funzione f mediante un polinomio P_n di grado al più n, che coincide con f negli n+1 punti x₀,x₁,…,x_n. Questo polinomio si chiama 'polinomio interpolatore di Lagrange', perché Lagrange (1795) l'aveva studiato scrivendolo nella forma:

Il primo a studiare rigorosamente l'errore di interpolazione fu Cauchy (1840). Egli dimostrò che l'errore è pari a:

dove ζ è un punto appartenente al più grande intervallo contenente i punti x₀,x₁,…,x_n e x. Per sfruttare i valori situati dall'altro lato di x₀ si possono utilizzare le differenze finite 'regressive' definite da ∇f_i=f_i−f_i−1 e ∇^mf_i=∇^m−1f_i−∇^m−1f_i−1 e la 'formula regressiva di Gregory-Newton':

Le formule di Gregory-Newton non sono completamente soddisfacenti per via della loro asimmetria. Per approssimare al meglio la funzione f in un intorno di x₀ sarebbe più opportuno sfruttare le due parti della tavola contemporaneamente. Con idonee operazioni di media sulle formule progressiva e regressiva di Gregory-Newton, gli astronomi costruirono formule di interpolazione più precise. Nella prima metà del XIX sec. le formule più utilizzate sono la 'formula di Newton-Stirling', che introduce una simmetria rispetto a un valore tabulato x₀, e la 'formula di Newton-Bessel', che introduce una simmetria rispetto al punto di mezzo fra due valori consecutivi x₀ e x₁. Queste formule, che utilizzano le 'differenze centrali' definite da δf_i=f_i+1/2−f_i−1/2 e δ^mf_i =δ^m−1f_i+1/2−δ^m−1f_i−1/2 si scrivono rispettivamente:

Oltre alla costruzione di tavole, un'applicazione essenziale dell'interpolazione riguarda le quadrature numeriche, cioè il calcolo approssimato degli integrali definiti. Dall'epoca di Newton, di Roger Cotes e di Thomas Simpson la tecnica di base consiste nel suddividere l'intervallo di integrazione in piccoli intervalli e nel sostituire in ciascun intervallo [a,b] la funzione integranda con il polinomio interpolatore che coincide con essa in un numero finito di punti, scelti in generale equidistanti e in modo simmetrico. Per un'interpolazione a uno, due, tre o quattro punti si ottengono le usuali regole dette 'del punto di mezzo' (o 'delle tangenti'), 'dei trapezi', 'di Simpson' e 'dei tre ottavi di Newton', che si scrivono rispettivamente:

Gli ingegneri, che non hanno bisogno di una grande precisione, si accontentavano di queste regole. In effetti, spesso calcolavano graficamente anche gli integrali, o per mezzo dei planimetri, che cominciano a fare la loro comparsa in quest'epoca, o decomponendo l'area sottesa dalla curva in piccoli rettangoli o trapezi che trasformano, con costruzioni grafiche, in un unico rettangolo o quadrato da misurare, ponendosi in tal modo nel solco di una lunga tradizione che risale all'Antichità. Va segnalato che Jean-Victor Poncelet, in particolare attraverso l'insegnamento che impartì presso l'École d'Application de l'Artillerie et du Génie di Metz a partire dal 1825, contribuì notevolmente al progresso delle pratiche di calcolo degli ingegneri. In primo luogo, sfruttando il fatto (di cui si è già detto sopra) che una funzione convessa è al di sotto delle sue corde e al di sopra delle sue tangenti, egli pensò di utilizzare contemporaneamente il metodo dei trapezi e quello del punto di mezzo per ottenere limitazioni per il valore dell'integrale e pertanto una valutazione dell'errore. Il procedimento, che consiste nel fare la media dei valori forniti dalla regola dei trapezi e delle tangenti, è noto da allora come 'metodo di Poncelet'. Inoltre, a proposito di un problema di stabilità delle volte (1835), Poncelet fu il primo a superare le vecchie suddivisioni in rettangoli e trapezi per definire un utile equivalente grafico del metodo di Simpson.

Nei calcoli astronomici, le regole elementari precedenti non bastano più. Si adoperano forme di quadratura più precise ottenute dall'integrazione della serie di interpolazione di Gregory-Newton con un maggior numero di termini (le 'formule di Newton-Cotes'). All'inizio del XIX sec. tuttavia, la scoperta di asteroidi che gravitano tra Marte e Giove, con orbite che hanno un'elevata inclinazione e una forte eccentricità, comporterà un salto qualitativo. Motivato dallo studio dell'asteroide Pallade, Gauss pensa di integrare le serie di interpolazione di Newton-Stirling e di Newton-Bessel per costruire formule di quadratura a convergenza più rapida. In effetti, per via della simmetria di queste due serie, le differenze finite di ordine dispari si annullano nell'integrazione. Gauss insegna queste nuove formule di quadratura numerica a Gottinga intorno al 1812 ed è uno dei suoi allievi, Johann Franz Encke, che le diffonde presso gli astronomi pubblicandole nel 1837. Legendre (1816) ritrova indipendentemente le stesse formule e se ne serve per la costruzione delle sue tavole di integrali ellittici.

Anche Pierre-Simon de Laplace, in tutti i suoi lavori di meccanica celeste e di calcolo delle probabilità, riflette a lungo sull'interpolazione e sulle quadrature numeriche. Ritrova i risultati precedenti e ne deriva di nuovi in modo molto formale, utilizzando serie generatrici e facendo un uso simbolico dell'operatore delle differenze Δ. Egli eccelle in particolare nell'arte di migliorare le formule classiche mediante l'aggiunta di termini correttivi che diminuiscono l'errore. Pressappoco nello stesso ordine di idee, Jacques-Frédéric Saigey (1859) definisce un metodo di accelerazione della convergenza a partire dal metodo dei trapezi, che prefigura lo schema di estrapolazione di Richardson-Romberg.

Ciò che precede riguarda essenzialmente l'interpolazione a partire da punti equidistanti, come è d'uso nelle tavole numeriche. Sarà sempre Gauss a orientare la ricerca sulle quadrature numeriche in una diversa direzione. Nel 1816 fornisce una diversa dimostrazione delle formule di Newton-Cotes e ne valuta la precisione osservando che, per n punti di interpolazione equidistanti e comprendenti gli estremi dell'intervallo, si ottiene una formula esatta per tutti i polinomi di grado minore o uguale a n−1. Gauss immagina allora di prendere n punti di interpolazione indipendenti nell'intervallo di integrazione, senza alcun vincolo a priori. Grazie agli n gradi di libertà così introdotti, egli trova condizioni su questi punti affinché la formula di quadratura sia esatta per tutti i polinomi di grado minore o uguale a 2n−1; ciò ottimizza l'approssimazione. Nel caso dell'intervallo [−1,1], al quale ci si può sempre ricondurre con un cambiamento di riferimento affine, gli n punti in questione sono le radici del polinomio di Legendre di grado n, definito dalla:

e le prime formule di Gauss per due e tre punti si scrivono, rispettivamente,

Jacobi (1826) dimostrò i risultati di Gauss in modo molto più semplice. Rehuel Lobatto (1852) ed Elwin Bruno Christoffel (1858) studiarono generalizzazioni al caso misto nel quale alcuni punti di interpolazione sono imposti e gli altri sono da scegliere in modo ottimale. In pratica, le formule di Gauss furono poco usate all'epoca: la presenza di irrazionali è infatti un handicap pesante nei calcoli a mano, ma sono nondimeno interessanti perché offrono la possibilità di ridurre della metà il numero delle misure fisiche da effettuare per ottenere una data precisione e ciò è fondamentale nel caso di misure costose. Infine, sul piano teorico, le formule di Gauss aprirono la strada a tutta una corrente di ricerche su varie famiglie di polinomi ortogonali. Pafnuty Lvovich Chebyshev (1854), studiando sistemi strutturati per convertire al meglio un moto rotatorio in un moto rettilineo nelle macchine a vapore, dimostrò che l'interpolazione di Lagrange nell'intervallo [−1,1] è ottimale nel senso dell'approssimazione uniforme quando gli n punti di interpolazione sono le radici del polinomio di Chebyshev di grado n, definito dalla:

Le ricerche concernenti i polinomi ortogonali e le loro applicazioni al calcolo numerico conosceranno un grande sviluppo dopo il 1870.

Equazioni differenziali e integrali

Numerosi fenomeni fisici, tecnici, biologici, economici, ecc., sono determinati una volta noti uno stato iniziale e una legge di evoluzione, a partire dai quali è possibile calcolare gli stati futuri. Matematicamente ciò si traduce in un 'problema di Cauchy', cioè in un'equazione differenziale ordinaria y′=f(x,y) e in una condizione iniziale y(x₀)=y₀ (in questa notazione, la lettera y può anche rappresentare una funzione vettoriale in uno spazio a p dimensioni; ciò permette di ricondurre alla stessa forma un sistema differenziale di p equazioni di ordine 1, o un'equazione differenziale scalare di ordine p).

Se si riesce a esprimere la soluzione esatta con un numero finito di quadrature, dal punto di vista del calcolo ci si riconduce a quadrature numeriche e alle tecniche ricordate sopra. Purtroppo è noto che la maggior parte delle equazioni differenziali non è risolubile per quadrature e pertanto occorre trovare altri metodi numerici. Gli astronomi, che dovevano continuamente risolvere sistemi differenziali a sei dimensioni (per descrivere il moto di un corpo celeste occorrono tre coordinate per la posizione e tre per la velocità; ovvero, con il metodo di Lagrange, i sei elementi orbitali dell'ellisse osculatrice di Kepler), pensarono di ricondursi in modo approssimato a un numero finito di quadrature. A questo scopo viene espresso il problema di Cauchy nella forma integrale equivalente:

e a partire da una prima soluzione approssimata y₁(x) (per es., quella fornita dal moto kepleriano trascurando le perturbazioni) si apportano le correzioni:

finché non vi sono più differenze sensibili. Pertanto a ogni passo ci si riduce a tante quadrature numeriche quante sono le dimensioni del sistema. Già Alexis-Claude Clairaut nel 1759 aveva proceduto in questo modo per prevedere il ritorno della cometa di Halley, utilizzando le formule di quadratura provenienti dalla serie di interpolazione di Gregory-Newton. Nel XIX sec., in seguito ai lavori di Gauss e di Encke, sono le formule di quadratura provenienti dalle serie di Newton-Stirling e di Newton-Bessel che diventano lo strumento comunemente usato dagli astronomi. Intorno al 1830 Cauchy e Joseph Liouville dimostrano la convergenza di questo metodo di approssimazioni successive e danno una valutazione dell'errore, ma soltanto nel caso delle equazioni differenziali lineari. Il caso generale sarà affrontato dal punto di vista teorico soltanto alla fine del XIX secolo.

Un altro approccio numerico al problema di Cauchy consiste nella 'discretizzazione' dell'equazione. La tecnica di base, nota come 'metodo di Euler', consiste nel prendere come curva integrale approssimata una linea poligonale, i cui vertici vengono costruiti gradualmente a partire da un punto iniziale, e nel sostituire l'equazione differenziale con un'equazione alle differenze finite. Ogni punto (x,y) è congiunto al punto seguente (x+Δx,y+Δy) da un segmento di retta, con una differenza Δy determinata esplicitamente dalla formula Δy=f(x,y)Δx o implicitamente dall'equazione Δy=f(x+Δx,y+Δy)Δx. I calcoli si possono fare numericamente o graficamente. Questa idea sarà ripresa e approfondita prima da Cauchy nei corsi all'école Polytechnique (1824), e poi in maniera indipendente da Rudolf Otto Sigismund Lipschitz (1868), per stabilire, con i nuovi criteri di rigore del XIX sec., il teorema fondamentale di esistenza detto di 'Cauchy-Lipschitz'. Inoltre, sempre dimostrando la convergenza delle linee poligonali di Euler verso una soluzione esatta quando il passo Δx tende a zero, Cauchy fornì anche una valutazione esplicita dell'errore.

Di fatto, a partire dal XVIII sec. il metodo di Euler non viene più usato. In effetti, si tratta di un metodo di ordine 1 e troppo poco preciso. Varianti del metodo del trapezio, di ordine 2, che consiste nel calcolare la media dei metodi di Euler ‒ metodo esplicito e implicito ‒ utilizzando a ogni passo l'equazione alle differenze:

sono introdotte in balistica da J.C.F. Otto (1842) e Isidore Didion (1848) per la compilazione delle tavole di artiglieria.

Si incontra anche, ma raramente perché il calcolo delle derivate successive è proibitivo, il metodo di Euler con uno sviluppo di Taylor spinto oltre il primo ordine, cioè:

Tutti questi algoritmi erano già stati descritti e utilizzati da Euler nel secolo precedente. Nel 1837 Gaspard-Gustave Coriolis, ispirandosi ai lavori di Cauchy, li studiò da un punto di vista teorico per determinare in particolare una valutazione dell'errore.

Oltre all'idea di sostituire la curva integrale con una successione di piccoli segmenti di tangenti, si pensa anche a utilizzare una successione di piccoli archi di cerchi osculatori. Il procedimento è particolarmente adatto a un'equazione del secondo ordine:

perché è noto che il raggio di curvatura di una curva soluzione è dato, posto dy/dx=tan α, dalla:

Sotto questa nuova forma l'equazione differenziale fornisce il raggio di curvatura in funzione della posizione del mobile e della direzione del moto. Si pensa dunque alla possibilità di ottenere, a partire da un punto iniziale nel quale si conosce l'inclinazione della tangente, una curva approssimata costruendo una successione di archi di cerchi osculatori. Tale metodo semigrafico è descritto per la prima volta da Sylvestre-François Lacroix (1814) e applicato concretamente da Poncelet (1829) al calcolo della traiettoria delle bombe. Didion (1848) ne sviluppò numerose varianti per la risoluzione di numerosi problemi di balistica esterna, tanto che esso è stato definito 'metodo di Poncelet-Didion'. La stessa tecnica fu impiegata per trattare il problema della capillarità. Intorno al 1855 William Thomson (lord Kelvin) integrò graficamente, a partire dai raggi di curvatura, l'equazione differenziale di Laplace per determinare la curva meridiana della superficie di rivoluzione formata da un liquido in un tubo o da una goccia di liquido su una superficie piana.

Per quanto riguarda le equazioni alle derivate parziali, le equazioni integrali e le equazioni funzionali più generali, vi sono tentativi sporadici di risoluzione, più o meno eterogenei, che talvolta prefigurano gli algoritmi moderni. È soprattutto dopo il 1870, però, che la trattazione numerica di questi problemi si sviluppa e si organizza, in particolare in seguito ai progressi dell'analisi funzionale.

Bibliografia

Aspray 1990: Computing before computers, edited by William Aspray, Ames, Iowa State University Press, 1990.

Chabert 1994: Histoire d'algorithmes. Du caillou à la puce, édité par Jean-Luc Chabert, Paris, Belin, 1994 (trad. ingl.: A history of algorithms. From the pebble to the microchip, translated by C. Weeks, New York, Springer, 1999).

Evesham 1986: Evesham, Harold Ainsley, Origins and development of nomography, "Annals of the history of computing", 8, 1986, pp. 324-333.

Fuller 1999: Fuller, A. Thomas, Horner versus Holdred. An episode in the history of root computation, "Historia mathematica", 26, 1999, pp. 29-51.

Goldstine 1977: Goldstine, Herman H., A history of numerical analysis from the 16th through the 19th century, New York, Springer, 1977.

Grattan-Guinness 1990: Grattan-Guinness, Ivor, Work for the hairdressers. The production of de Prony's logarithmic and trigonometric tables, "Annals of the history of computing", 12, 1990, pp. 177-185.

Marguin 1994: Marguin, Jean, Histoire des instruments et machines à calculer. Trois siècles de mécanique pensante, 1642-1942, Paris, Hermann, 1994.

Prange 1904-35: Prange, Georg, Die allgemeinen Integrationsmethoden der analytischen Mechanik, in: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. IV/2: Mechanik, redigiert von Felix Klein und Conrad Müller, 1904-1935, pp. 505-804.

Pulte 2002: Pulte, Helmut - Thiele, Rüdiger, Meccanica variazionale, in: Storia della scienza, diretta da Sandro Petruccioli, Roma, Istituto della Enciclopedia Italiana, 2001-; v. VI, 2002, pp. 453-461.

Tournès 1998: Tournès, Dominique, L'origine des méthodes multipas pour l'intégration numérique des équations différentielles ordinaires, "Revue d'histoire des mathématiques", 4, 1998, pp. 5-72.

‒ 2000: Tournès, Dominique, Pour une histoire du calcul graphique, "Revue d'histoire des mathématiques", 6, 2000, pp. 127-161.