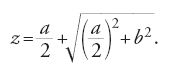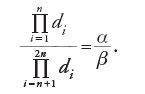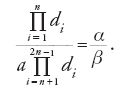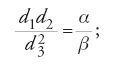La Rivoluzione scientifica: i domini della conoscenza. La rivoluzione cartesiana e gli sviluppi della geometria
Storia della Scienza (2002)
La Rivoluzione scientifica: i domini della conoscenza. La rivoluzione cartesiana e gli sviluppi della geometria
La rivoluzione cartesiana e gli sviluppi della geometria
La rivoluzione cartesiana
La Géométrie di René Descartes, pubblicata nel 1637, modificò radicalmente la concezione e la pratica della geometria. Le caratteristiche di questo testo fondamentale devono dunque essere interpretate e valutate alla luce della matematica greca classica e, soprattutto, di quella del Tardo Medioevo e del Rinascimento. È in quest'epoca, infatti, che comincia a essere sottoposta a una parziale revisione la divisione classica delle matematiche in due settori nettamente separati: quello della geometria, regno delle figure, e quello dell'aritmetica, mondo dei numeri.
Verso la metà del XV sec. due eventi simultanei ‒ la fine dell'Impero bizantino e l'invenzione della stampa ‒ misero a disposizione della comunità scientifica traduzioni latine di trattati di geometria greca fino ad allora sconosciuti. Nella prima metà del XVI sec. la geometria non si distaccò molto da Euclide (gli Elementi furono tradotti, commentati e stampati innumerevoli volte); ma, a partire dalla seconda metà del secolo, Federico Commandino pubblicò le traduzioni latine di Archimede (1558), Apollonio (1566) e Pappo (1588). L'influsso di queste idee geometriche si scontrava con un movimento di pensiero che si era sviluppato in senso quasi opposto. Nel Medioevo (in particolare nel XII sec. in Spagna e nel XIII in Italia) si era affermato il sistema di numerazione arabo e avevano avuto diffusione gli sviluppi nel campo dell'algebra (codificati nel IX sec. nei trattati di Mūsā al-Ḫwārazmī). Tra la metà e la fine del XVI sec., l'algebra conobbe una grande fioritura grazie all'opera di tre importanti studiosi italiani: Niccolò Tartaglia, Gerolamo Cardano e Raffaele Bombelli. L'uso, ancorché parziale, di notazioni simboliche rese possibile ricavare la soluzione generale delle equazioni di terzo e quarto grado, fatto che conduceva naturalmente alla ricerca delle soluzioni per le equazioni di quinto grado e ‒ più in generale ‒ per equazioni polinomiali di grado qualsiasi. La soluzione delle equazioni per radicali (ottenere espressioni che permettano di esprimere le radici di un'equazione in funzione dei coefficienti e con formule che contengano solo le quattro operazioni aritmetiche e l'estrazione di radici) era un programma di ricerca ben definito, anche se nessuno poteva allora immaginare le difficoltà che avrebbe comportato.
L'evoluzione dell'algebra da un approccio sostanzialmente orientato alla soluzione di problemi a uno più simbolico e astratto comportò una trasformazione dell'utilizzazione di questa disciplina, insieme con un cambiamento del suo oggetto. Sebbene all'inizio fosse impiegata in problemi di natura numerica, l'algebra cominciò a essere applicata anche nello studio di problemi geometrici e, man mano che si sviluppava una notazione astratta per le variabili e le costanti, andò trasformandosi in una scienza delle grandezze astratte in generale, in una mathesis universalis. Questa crescente ambivalenza dell'algebra provocò un cambiamento nel modo di concepire le figure geometriche e i numeri. Fu questa trasformazione che, in ultima analisi, condusse nel XIX sec. alla creazione della retta dei numeri reali, un ibrido di aritmetica e geometria.
Anche un altro orientamento ‒ dovuto all'imporsi di problemi pratici nel campo della matematica ‒ spinse gli studiosi del Rinascimento a considerare numero e figura come un'unica entità invece di due separate. Fra questi problemi c'erano il calcolo dei tassi d'interesse e di cambio delle varie valute, lo studio della prospettiva, la compilazione di mappe per l'agrimensura e la navigazione, l'analisi delle traiettorie in meccanica, il perfezionamento degli orologi, lo sviluppo della trigonometria e l'introduzione dei logaritmi. La crescente consapevolezza dell'applicabilità della matematica a situazioni pratiche stimolò l'interesse nei confronti dei rapporti tra forma astratta e caso concreto, tra indeterminato (ma comunque formale) e determinato; i matematici furono quindi costretti a ricercare mezzi di espressione sempre più generali e sempre più in grado di chiarire le relazioni tra gli oggetti: in grado, cioè, di collegare casi diversi rendendo esplicita la struttura relazionale comune.
All'inizio del XVII sec., dunque, la geometria non solo era oggetto di rinnovato interesse, ma stava subendo una trasformazione, anche se la fusione di geometria, aritmetica e algebra presentava molte difficoltà. D'altronde, vi erano profonde differenze fra i metodi dell'aritmetica e quelli della geometria: in particolare la moltiplicazione e la divisione erano collegate da analogie poco chiare, piuttosto limitate e poco promettenti. Il prodotto di due segmenti era interpretato come un'area e quello di tre come un volume: la moltiplicazione coinvolgeva un cambio di dimensione e oltretutto, nel caso di più di tre dimensioni, non poteva essere né rappresentata, né interpretata intuitivamente. La divisione, dal canto suo, veniva spesso considerata come rapporto, cioè come una relazione: questo implicava che il risultato della divisione non fosse visto come una grandezza. Nonostante queste difficoltà, i matematici erano sempre più interessati all'applicazione dell'algebra e all'uso dei numeri nei problemi di analisi geometrica. Simon Stevin, uno dei primi a sviluppare la notazione decimale, sostenne in maniera molto convinta, nell'Arithmétique (1585), che i numeri erano mezzi adeguati per trattare le grandezze continue (in particolare quelle geometriche). Stevin arrivò ad affermare che le difficoltà che derivavano dal considerare le grandezze irrazionali come numeri potevano essere eliminate tramite un uso più sistematico dei numeri in geometria (proponendo così un programma che fu realizzato solo nel XIX sec.); ma sostenne anche che, siccome le approssimazioni sono adeguate ai bisogni della matematica applicata, i matematici non avrebbero dovuto rifiutarsi di usarle. Descartes fece suo il nuovo strumento algebrico nella Géométrie, evitando completamente di affrontare la questione del numero.
L'opera di François Viète (1540-1603), forse il più importante precursore di Descartes, si sviluppò da questa confluenza fra algebra e geometria. Per Viète l'algebra consisteva nello studio della grandezza astratta, termine con il quale indicava sia la grandezza geometrica sia il numero, considerato come un tipo di grandezza. Egli fu tra i primi a indicare le grandezze con lettere e a distinguerle all'interno di un'equazione in incognite o indeterminate ‒ designate con vocali ‒, e grandezze note (parametri) ‒ indicate con le consonanti. Non si trattava di una notazione compiutamente simbolica, dato che comparivano ancora parole latine, come in per indicare la moltiplicazione e termini come cubus, quadratus, aequalis; tale notazione, tuttavia, era più che sufficiente per sviluppare il suo programma algebrico della soluzione delle equazioni per radicali: per quanto riguarda la teoria delle equazioni, Viète arrivò molto vicino all'introduzione delle funzioni simmetriche delle radici. Tuttavia, dato che considerava solo radici positive, non si rese conto che un'equazione può avere tante radici quanto è il suo grado.
Inoltre, dal momento che conosceva bene le opere di Apollonio e Pappo, iniziò ad affrontare il problema geometrico della costruzione delle equazioni: determinare cioè procedure geometriche che permettessero di ottenere segmenti di lunghezza uguale alle radici di un'equazione polinomiale in un'incognita, un progetto che fu fatto proprio da Descartes. La più importante conseguenza dell'esplorazione vietiana delle forme algebriche in relazione con la geometria fu l'intuizione che ogni problema geometrico, se è traducibile algebricamente in un'equazione di terzo o quarto grado, può essere ridotto o alla trisezione dell'angolo o all'inserzione di due medie proporzionali (cioè di due medie geometriche tra due grandezze date). Fu dunque in grado di collegare l'innovativa manipolazione algebrica dell'aritmetica ad alcuni dei più raffinati risultati della geometria greca.
Viète aveva però introdotto un limite formale nella sua trattazione algebrica delle grandezze astratte. Infatti, interpretava la moltiplicazione seguendo gli schemi della geometria classica, per la quale la moltiplicazione di due segmenti, per esempio, produce un rettangolo e quindi implica un cambio di dimensione. Viète si limitò a generalizzare: ogni grandezza era inserita in una scala i cui gradini erano 'specie' di grandezze di dimensione più alta o più bassa, che chiamò i 'gradi' della grandezza. All'interno della scala solo le grandezze dello stesso grado potevano essere sommate, sottratte o confrontate; questa era la legge di omogeneità. Il prodotto di una grandezza di grado n e una di grado m era di grado (n+m); una grandezza poteva essere divisa da una di dimensione minore, e la dimensione del quoziente era la differenza fra le due. Il quoziente però non era la stessa cosa del rapporto, in quanto il rapporto è una relazione che si può avere solo fra grandezze della stessa dimensione. Così anche l'estrazione di radice poteva essere effettuata solo su grandezze di dimensione appropriata: per esempio, la radice cubica poteva essere trovata solo per una grandezza 'solida', di terzo grado. Nonostante queste limitazioni, l'approccio vietiano schiuse un intero nuovo campo di ricerche geometriche, mostrando come problemi più complessi di quelli costruibili con riga e compasso non fossero solo casi isolati ed eccezionali, ma costituissero una notevole schiera di quesiti, che potevano essere posti in relazione sistematica gli uni con gli altri, e la cui soluzione, senza dubbio, richiedeva metodi completamente nuovi.
Ci si può chiedere come mai nella ricerca matematica di Descartes il problema della costruzione geometrica delle radici delle equazioni occupasse un posto tanto rilevante; o, allo stesso modo, perché si ispirasse più a Pappo che ad Archimede. Possiamo dire che i due grandi cambiamenti che si verificano nella matematica all'inizio del XVII sec. sono, da una parte, l'algebrizzazione e, dall'altra, le tendenze che sfoceranno più tardi nel calcolo infinitesimale. Galilei, per esempio, fu più interessato a quest'ultimo aspetto e il suo modo di affrontare lo studio del moto influenzò direttamente i lavori dei suoi discepoli Bonaventura Cavalieri ed Evangelista Torricelli, i quali svilupparono metodi e concetti che avrebbero poi contribuito alla nascita del calcolo infinitesimale e della sua applicazione ai problemi della meccanica. Descartes riteneva, non meno di Galilei, che lo studio della Natura avesse implicazioni a livello filosofico e le sue riflessioni su questo tema contribuirono notevolmente all'impatto rivoluzionario dei suoi lavori. Tuttavia i suoi interessi matematici furono orientati soprattutto verso problemi di forma o, meglio, di configurazione, e non verso quelli di trasformazione o processo. Questa preferenza può essere spiegata meglio tenendo conto della concezione cartesiana del metodo e del suo impegno in questo senso.
L'interesse di Descartes per il metodo pervade tutta la sua opera, e questo implica che nessuno dei suoi scritti può essere adeguatamente compreso se esaminato singolarmente. Il Discours de la méthode fu pubblicato per la prima volta nel 1637 come introduzione ai tre trattati scientifico-matematici "qui sont des essais de cette méthode": uno di essi era proprio la Géométrie. Nel Discours c'è un précis delle argomentazioni che saranno sviluppate nelle Meditationes de prima philosophia (1641) e che verranno ricapitolate all'inizio dei Principia philosophiae (1644). Descartes, dunque, colloca con molta attenzione la sua matematica e la sua fisica: secondo l'ordine metodologico della ragione, gli argomenti delle Meditationes le precedono e forniscono loro legittimazione e giustificazione metafisica. Il metodo cartesiano è, prima di tutto, intuizionista: rende esplicito il modo attraverso cui l'oggetto della conoscenza viene percepito dal soggetto della conoscenza. Ogni filosofo intuizionista ‒ Epicuro come Kant e lo stesso Descartes ‒ propone un canone della rappresentazione, per criticare e correggere l'assunzione dogmatica che esistano asserzioni capaci di registrare la verità di oggetti dati a prescindere da qualsiasi attività del soggetto. L'adeguazione intuizionista tende piuttosto a identificare la rappresentazione con la procedura canonica della sua costruzione come oggetto di conoscenza. Per Descartes, il canone della costruibilità è il suo metodo: critico, finitista e costruttivista; tale metodo disegna una sfera in cui la conoscenza umana può essere estesa in modo attendibile, ma oltre la quale non può avventurarsi. È da qui che trae origine la distinzione che Descartes opera fra curve algebriche e curve trascendenti, le une da includere nella geometria, le altre, invece, da bandire.
Il canone intuizionista cartesiano è inoltre riduzionista. Il metodo cartesiano colloca l'oggetto della conoscenza in un dato ambito e i vari ambiti all'interno della sfera della conoscenza umana considerata come un tutto, secondo un 'ordine della ragione' che comincia con le idee chiare, distinte, indubitabili e di per sé evidenti, e prosegue attraverso una catena di ragionamenti che conservino e amplino la verità. Un'altra formulazione dell''ordine della ragione' è che il dispiegarsi della conoscenza deve cominciare con le cose semplici, che sono di per sé trasparenti alla ragione, e svilupparsi solo attraverso un canone costruttivo che, collegando le cose semplici, permetta di giungere a quelle più complesse. Dunque si spera ‒ e, in modo meno immediato, si sa ‒ che una situazione complessa possa sempre essere ricondotta agli oggetti semplici dai quali è scaturita. Descartes presenta gli oggetti semplici e il suo metodo relazionale di collegarli come se fossero ovvi, unici e trasparenti, senza alcuna giustificazione; assume inoltre che le cose semplici e quelle complesse siano omogenee, in senso forte.
Da un certo punto di vista, furono proprio queste assunzioni riduzioniste la chiave del successo matematico di Descartes. Secondo il ragionamento illustrato nella Géométrie i punti di partenza ‒ gli 'oggetti semplici' ‒ della geometria sono i segmenti di retta: "Tutti i problemi della geometria possono facilmente esser riportati a termini tali che poi, per costruirli, non c'è da conoscere che la lunghezza di alcune rette" (OS, II, pp. 528-529).
La spinta riduzionista del suo metodo lo rese un meraviglioso strumento per la soluzione dei problemi. Il passo successivo consiste infatti nella rivelazione che il prodotto e la divisione di segmenti devono anch'essi venire interpretati come segmenti. La sua algebra delle grandezze geometriche è dunque chiusa; con una brillante intuizione l'algebra applicata alle grandezze è liberata dagli impedimenti e dalle complicazioni che avevano ostacolato Viète. La regola di costruzione (come si combinano le entità più semplici) è prodotta principalmente dalla sua interpretazione delle operazioni aritmetiche, compresa l'estrazione di radice, e quindi dal metodo per costruire problemi algebricamente più complessi a partire dalle soluzioni dei problemi più semplici; proseguendo con questa gerarchia, Descartes fornisce anche metodi per costruire curve algebricamente più complesse a partire da quelle più semplici.
Ma questa valutazione del successo di Descartes deve subito essere un po' sfumata, poiché per molti aspetti egli non segue i criteri riduzionisti; per di più è il suo stesso riduzionismo a intralciare le sue scoperte matematiche. In ogni costruzione, è costretto a introdurre indebitamente entità (in particolare curve) non perfettamente adeguate a quel livello della costruzione; il suo 'punto di partenza', il segmento, richiede che siano disponibili delle curve come mezzo di costruzione, così come in seguito per ottenere certe curve più complicate ci sarà bisogno di costruirne altre tecnicamente non ancora disponibili. La regola di costruzione risulta essere una composizione di strumenti algebrici, geometrici e meccanici che Descartes non è in grado di collegare completamente in maniera razionale. In effetti, la stabilità concettuale di alcuni degli oggetti più complicati della sua nuova geometria è minacciata proprio dal suo metodo riduzionista e dal modo col quale tende a dividere le cose nelle loro entità più semplici. Infine, cosa più importante, i limiti del suo metodo (soprattutto il requisito forte dell'omogeneità tra cose semplici e complesse, e della rigidità della regola di costruzione) gli impedirono di addentrarsi in importanti ambiti che i suoi successori immediati cominciarono a esplorare. Descartes non comprese appieno il valore della nuova algebra che aveva creato; non arrivò mai, infatti, ad apprezzarla completamente, né come strumento ambivalente per 'unificare' (secondo una concezione profondamente innovativa di tale unificazione) i due mondi eterogenei del numero e della figura, né come fonte di nuovi oggetti matematici quali polinomi, curve e serie infinite.
Il contrasto con Pierre de Fermat è centrale per comprendere la questione. Fermat sviluppa una geometria algebrizzata più o meno nello stesso periodo di Descartes, esponendola nell'opera Ad locos planos et solidos isagoge (pubblicata nel 1679, ma che circolava fin dal 1637). Egli mostra, pur senza sfruttarlo fino in fondo, il potere dell'algebra nello stabilire analogie tra numero e figura geometrica, mettendo in evidenza la rappresentazione delle equazioni indeterminate in due variabili ed elaborando nei dettagli le relazioni fra equazioni, luoghi e curve. Fermat comincia la sua esposizione rappresentando il caso più semplice, l'equazione lineare ax=by, dimostrando che si tratta sempre di una retta e che, di conseguenza, ogni equazione di primo grado in due incognite rappresenta una retta. Prosegue, quindi, fornendo un'analisi esaustiva dei vari casi delle equazioni di secondo grado in due incognite, e delle curve (le coniche) associate a esse; considera inoltre una linea delle ordinate perpendicolare a quella delle ascisse; semplifica la forma delle equazioni con rotazioni e traslazioni degli assi.
La Géométrie cartesiana, invece, dedica molto spazio (specialmente nei Libri I e III) alla costruzione delle radici delle equazioni in un'incognita sola; la costruzione cioè di un nuovo segmento sulla base di una relazione data fra segmenti. Il modo in cui Descartes sceglie gli assi e le equazioni dipende sempre dalla configurazione geometrica del problema dato. L'esplorazione dell'analogia tra configurazioni geometriche e modelli numerici l'avrebbe portato a sollevare l'imbarazzante problema delle grandezze irrazionali e della loro eterogeneità rispetto ai numeri razionali. è dunque Fermat, più che Descartes, a sfruttare l'ambivalenza della notazione algebrica. John Wallis, nell'Arithmetica infinitorum del 1655 e nella Mathesis universalis del 1657 affronterà problemi algebrici in termini tanto di figura geometrica quanto di modello di numero, muovendosi liberamente (per non dire disinvoltamente) tra i due settori; sarà Leibniz, una generazione dopo, ad adoperare ed estendere la nuova algebra per dominare e riorganizzare l'aritmetica, la geometria e la meccanica, arrivando ad affrontare lo studio delle proprietà formali dei polinomi, delle serie infinite e delle equazioni differenziali.
La 'Géométrie'
Lo scopo principale della Géométrie è quello di presentare la geometria come un campo di problemi di costruzione, ordinato in modo tale che questi possono essere risolti non con la semplice abilità ma con un metodo; l'algebra è importante per le risorse e l'ordine che offre, ma svolge un ruolo ausiliario. I problemi più semplici sono quelli ereditati dal canone della geometria greca; per esempio, dati due segmenti, costruire la loro media proporzionale. I tre famosi problemi dell'Antichità erano: la quadratura del cerchio, la duplicazione del cubo e la trisezione dell'angolo. Secondo l'interpretazione di Viète della geometria greca ‒ che Descartes segue ‒, le costruzioni con riga e compasso sono le più rigorose e ben definite. Ovviamente, però, i tre problemi suddetti non possono essere risolti solo con intersezioni di rette e cerchi, le curve che, secondo Viète, erano le sole accettate dai Greci come 'curve da costruzione'. Secondo Descartes, un problema geometrico doveva venir tradotto in un'equazione algebrica in un'incognita; le radici dell'equazione dovevano poi essere costruite utilizzando mezzi geometrici accettabili. Le 'curve da costruzione' che egli ammette e cataloga sono le coniche e alcune cubiche, ma prevede anche l'uso di curve algebriche di ordine superiore.
La necessità di precisare cosa intendesse con 'complessità crescente' costrinse Descartes a considerare vari e insoliti strumenti meccanici per tracciare le curve, a studiare le proprietà delle curve stesse e a indagare la struttura delle equazioni algebriche associate sia ai problemi sia alle curve. Diversi studiosi hanno sottolineato questa sorta di fascinazione verso gli strumenti per disegnare, le curve e le equazioni, discutendo se Descartes debba essere considerato un geometra che si pone al termine di una lunga tradizione (Boyer 1956, Lenoir 1979, Bos 1981, Lachterman 1989) o un algebrista che intraprende una nuova strada (Giusti 1990, Mancosu 1996). Forse sarebbe più giusto sostenere che non fu nessuna delle due cose (Grosholz 1991, Bos 2001). Descartes non assomiglia a Euclide, che vedeva la geometria come lo studio di certi oggetti, né a David Hilbert (1862-1943), che sosteneva ‒ ma non sempre ‒ che la geometria è qualunque cosa possa costituire un modello di un dato sistema formale, deduttivo e assiomatizzato. Il Descartes matematico è una figura di transizione. Il suo metodo è riduzionista: per lui, la geometria è lo studio della costruzione di segmenti sulla base di altri segmenti dati, che stanno in certe determinate relazioni gli uni con gli altri. Curve da una parte ed equazioni dall'altra hanno un ruolo in questa visione, ma il loro posto non è al centro della scena.
Nella Géométrie Descartes affronta così in un programma di classificazione dei problemi secondo la complessità delle curve necessarie per la loro costruzione. Per prima cosa deve stabilire quali curve siano accettabili nelle costruzioni. In secondo luogo deve trovare un criterio per ordinarle. Infine, deve mostrare come scegliere, per un dato tipo di problema, la più semplice delle 'curve da costruzione'. Sperava insomma di fornire, usando l'algebra come mezzo per analizzare i problemi, un metodo generale per ricavare le costruzioni di ogni problema sorto nella tradizione geometrica e, nello stesso tempo, d'identificare e ordinare tutti i mezzi necessari per queste costruzioni che andassero al di là della riga e del compasso. In fin dei conti, egli riuscì più o meno a realizzare ciò che si era proposto.
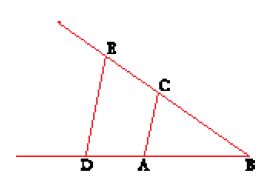
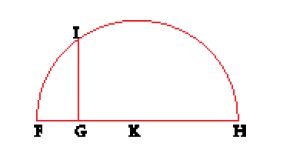
Proprio nelle prime pagine della Géométrie, Descartes dimostra come le operazioni di addizione, sottrazione, moltiplicazione, divisione ed estrazione di radice quadrata possano essere interpretate geometricamente, come operazioni su segmenti che producono ancora segmenti. L''ordine della ragione' impone che la geometria cominci con i segmenti e avanzi verso entità più complesse attraverso operazioni successive. L'addizione e la sottrazione sono semplici. La moltiplicazione e la divisione sono illustrate dalla fig. 5. Per moltiplicare BD per BC, si prende AB come unità; si uniscono i punti A e C e si traccia DE parallela a CA; allora BE è il prodotto di BD per BC. Per dividere BE per BD, si uniscono E e D e si traccia AC parallela a DE ; il segmento BC sarà allora il quoziente. Il caso della radice quadrata è illustrato nella fig. 6. Per trovare la radice quadrata di GH, si aggiunge a questo segmento un segmento uguale all'unità, FG; si biseca poi FH nel punto K e si descrive la semicirconferenza FIH di centro K. Si traccia ora la perpendicolare a FH in G, che interseca il cerchio in I: la radice richiesta è GI.
Descartes non dice nulla sulla sua scelta dei segmenti come punti di partenza semplici, né sul motivo per cui ha escluso le aree, le curve, i numeri, gli angoli e le grandezze infinitesimali dai rapporti e dalle proporzioni, né si esprime riguardo a come una teoria di questi oggetti stia in relazione all''ordine della ragione' e, dunque, all'algebra dell'aritmetica. È proprio questo aspetto intuizionista della dottrina cartesiana che Leibniz non trova convincente, vale a dire l'assunto che punti di partenza 'chiari e distinti' non richiedano ulteriori giustificazioni. La pretesa priorità di questi punti di partenza, i segmenti, serve a celare il debito di Descartes verso la geometria greca e l'esclusione degli sviluppi a lui contemporanei. Nasconde inoltre una circolarità nel procedere del suo ragionamento: l'introduzione delle linee curve deve essere successiva a quella dei segmenti. Ma, come abbiamo già visto, per ottenere i prodotti, i quozienti e la radice quadrata è necessario l'uso del cerchio come curva da costruzione; la costruzione di altre radici richiede dunque curve di grado algebrico superiore.
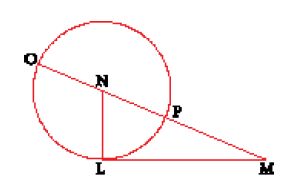
Descartes non spiega mai quale collegamento vi sia fra la teoria greca delle proporzioni e l'algebra delle equazioni. Semplicemente, esprime la relazione tra i problemi geometrici, enunciati in termini di rapporti e proporzioni, e le equazioni algebriche, spiegando come un geometra possa usare l'interpretazione delle operazioni per ricavare un'equazione algebrica, la cui soluzione fornirà la risposta al problema. La costruzione di problemi piani per mezzo dell'algebra è esemplificata nella fig. 7. Un problema che può essere costruito con riga e compasso si può esprimere con un'equazione di secondo grado a una sola incognita: il quadrato di una quantità incognita posto uguale al prodotto della sua radice per una quantità nota, aumentato o diminuito di una qualche altra quantità sempre nota. La fig. 7 rappresenta un problema espresso da z2=az+b2. Il lato LM del triangolo rettangolo NLM è uguale a b (la radice quadrata della quantità nota b2) e l'altro lato LN è uguale alla metà di a. Si prolunghi ora MN fino a O, in modo tale che NO sia uguale a NL. Il segmento OM sarà quindi uguale a z, che era quello che cercavamo, la radice dell'equazione. Una semplice applicazione del teorema di Pitagora dimostra che questa costruzione è espressa dalla seguente formula:
Notiamo che questa costruzione richiede la possibilità di usare il cerchio come curva da costruzione, e la validità del teorema di Pitagora, che coinvolge i triangoli; in quale posizione dovrebbero essere sistemati questi oggetti nell''ordine della ragione'? A questo punto Descartes si trova di fronte due possibili modi di generalizzare il suo approccio. Il primo è quello di passare a trattare problemi la cui espressione algebrica richieda non più una sola, ma due variabili. Descartes lo sviluppa discutendo il 'problema di Pappo', una famiglia di problemi nei quali ciò che deve essere costruito non è più un singolo punto (come per es. i punti O o I nelle due figure precedenti) e quindi un segmento determinato da esso, ma un luogo, che deve essere costruito per punti. Il secondo modo comporta la generalizzazione del suo approccio a problemi la cui espressione algebrica richieda esponenti maggiori di due; quando il grado dell'equazione è per esempio tre o quattro, vi sono formule generali per le radici, che però richiedono l'estrazione della radice cubica, operazione che non può essere fatta solo con l'uso di riga e compasso. Anche questo aspetto può essere illustrato dal teorema di Pappo.
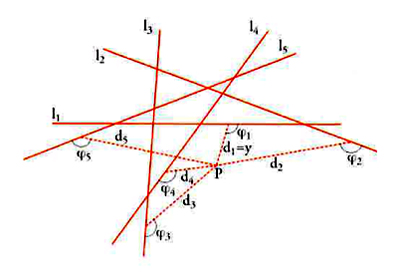
Descartes conobbe il problema di Pappo nel 1631, grazie a un matematico e orientalista olandese, Jacob Gool (Golius), il quale pensava che Descartes potesse essere interessato a sperimentare il suo nuovo metodo su di esso. Nel Libro VII delle Collectiones mathematicae, Pappo aveva proposto una sorta di generalizzazione di un problema che circolava fin dai tempi di Euclide, e che implicava una nuova classe di curve. Trattandosi di un problema che i matematici greci non avevano potuto risolvere in maniera metodica né avevano saputo generalizzare adeguatamente, si prestava assai bene a dimostrare la potenza del metodo cartesiano. Si tratta di determinare un luogo i cui punti P soddisfino una delle condizioni illustrate nella fig. 8. Sia di la lunghezza del segmento da P alla retta li (data), e sia φi l'angolo (anch'esso dato) che il segmento forma con la retta li. Sia ora α/β un rapporto dato e a un segmento dato. Il problema è trovare i punti P che soddisfino la seguente condizione: se il numero delle linee li, 'date in posizione', è pari (2n), il rapporto fra il prodotto delle prime n lunghezze di e il prodotto delle rimanenti n deve essere uguale al rapporto dato α/β, con α e β segmenti arbitrari; in formule:
Se il numero delle linee li 'date in posizione' è dispari (2n−1), il rapporto fra il prodotto delle prime n lunghezze di e il prodotto delle rimanenti n−1 per una lunghezza fissata a deve essere uguale al rapporto α/β; in formule:
vi sono infatti dei punti che soddisfano ognuna di queste condizioni e che formano, quindi, un luogo nel piano.
Da quanto riferisce Pappo, sembra che Apollonio avesse studiato questo problema, facendo uso di una tecnica chiamata 'applicazione delle aree', grazie alla quale riduceva il problema dato a una trasformazione geometrica di aree. Di conseguenza, quasi come un sottoprodotto del problema principale ‒ la determinazione di luoghi ‒ egli puntò a esprimere equivalenze fra aree (come nel caso delle quattro linee) in una forma il più possibile semplice e compatta. Poiché i Greci interpretavano il prodotto di due e di tre segmenti rispettivamente come un'area e un volume, l'applicazione delle aree non era utilizzabile nel caso con più di sei linee. Pappo, presentando il lavoro di Apollonio, sottolinea come si presenti complessa la generalizzazione del problema oltre le sei linee, suggerendo che si potrebbe forse procedere attraverso l'uso del rapporto composto, una sorta di 'moltiplicazione' di rapporti. Questa limitazione della matematica greca rivela le innovazioni insite nella definizione cartesiana delle operazioni aritmetiche per mezzo di segmenti, in quanto le somme, le differenze, i prodotti, le divisioni e le radici sono interpretate ancora come segmenti: cioè la sua algebra è chiusa e i suoi elementi sono tutti omogenei.
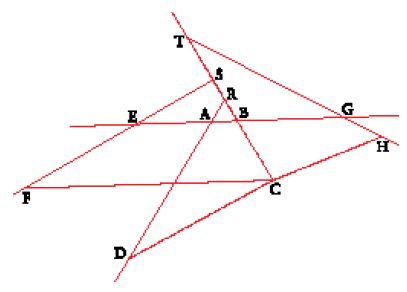
Verso la metà del primo libro della Géométrie, Descartes annuncia: "Mi pare di aver così interamente soddisfatto alle ricerche che, secondo Pappo, gli antichi avevano impostato in questo campo" (OS, II, p. 552), come se avesse risolto il problema in modo completo per un qualsiasi numero di linee. Ma anche se è vero che la combinazione di metodi geometrici e aritmetico-algebrici fornisce un importante sviluppo verso la soluzione del problema, ciò non significa che esso sia stato risolto completamente. Infatti sono presenti importanti e inaspettate complicazioni riguardo alle curve geometriche, alle equazioni polinomiali e al concetto stesso di numero (anche se Descartes pare non considerare affatto quest'ultimo aspetto) nonché ai loro collegamenti. È alla fine del primo libro che si trova la spiegazione del metodo per risolvere la famiglia di problemi definita dal problema di Pappo, accompagnata da una figura relativa al problema delle quattro linee (fig. 9).
Descartes comincia con l'analisi del problema, trattandolo cioè come se fosse già risolto e riducendo la complessità della figura: "considero una delle rette date e una di quelle che bisogna trovare, per esempio AB e CB, come le principali", le linee, cioè, attraverso le quali dovranno essere espresse tutte le altre. In altre parole, tutte le linee devono ricevere un nome e i segmenti noti devono essere attentamente distinti da quelli che cerchiamo; dobbiamo inoltre scrivere tutte le equazioni che esprimono le relazioni fra i segmenti noti e incogniti. Egli sceglie così di chiamare y il segmento BC (d1) e x il segmento AB, e quindi dimostra che tutti gli altri di possono essere espressi linearmente in x e y. Nel caso in cui si abbiano 2n linee, l'equazione sarà di grado al più n; per 2n−1 linee, sarà di grado al più n, ma la potenza di x sarà al massimo n−1. Nel caso di 2n e 2n−1 linee parallele solo la variabile y è coinvolta e il risultato che si ottiene è un'equazione in y di grado al più n.
La costruzione per punti del luogo si ricava come segue: si sceglie un valore per y e si sostituisce nell'equazione, ottenendo così un'equazione in una sola incognita, x. Per il caso delle tre linee, l'equazione in x è in generale di grado 2; per 2n linee, è di grado al più n; per 2n−1 linee, è di grado al più n−1. Nel caso di 2n−1 linee parallele l'equazione ha già una sola variabile, y, ed è di grado n. Le radici di questa equazione possono essere costruite per mezzo d'intersezioni di curve da determinare. Questa procedura genera la curva punto per punto e dunque è potenzialmente infinita, come Descartes nota: "Ancora, prendendo successivamente infinite grandezze diverse per la linea y, ne troveremo pure infinite per la linea x, e così si avrà un'infinità di punti diversi, come il punto C, per mezzo dei quali si descriverà la linea curva richiesta" (ibidem, pp. 552-557).
Parrebbe dunque che il problema di Pappo sia stato ridotto a determinare la costruzione geometrica delle radici delle equazioni in una incognita: la costruzione di segmenti in base a relazioni razionali tra altri segmenti.
Comunque, questa riduzione ha uno strano effetto sulla valutazione che Descartes dà dei risultati da lui stesso ottenuti. Una delle prime cose che afferma riguardo al problema di Pappo è che ha trovato un modo per classificare i vari casi dei problemi. Ma questa classificazione non si basa su una qualche caratteristica del luogo generato (come l'approccio fermatiano e una visione moderna del progetto cartesiano ci indurrebbero a ritenere), quanto piuttosto su quale tipo di 'curva da costruzione' si debba scegliere per ottenere la costruzione per punti del luogo: quella cioè del segmento x, una volta ottenuta l'equazione in x e y e fissato il valore della y. Descartes riprende questa classificazione dei vari casi proprio alla fine del Libro I in una forma più esplicitamente algebrica; essa non si riferisce alle curve (descrivibili per mezzo di equazioni indeterminate a due incognite), ma a problemi (descrivibili per mezzo di equazioni determinate a una incognita). Notiamo che la fig. 9 non contiene alcun riferimento al luogo cercato, ma in essa compaiono solo i collegamenti dei segmenti e le loro relazioni con un punto arbitrario C appartenente al luogo. Sembrerebbe quasi che queste figure si occupino solo di segmenti; anche la costruzione della curva interviene, ma la scelta di queste curve non viene per il momento discussa e la figura non le riguarda.
è nel Libro II che si trova un tentativo di classificazione delle curve a seconda della loro attitudine a essere utilizzate come curve da costruzione:
Gli antichi hanno osservato molto giustamente che i Problemi di Geometria sono o piani o solidi o lineari. Ciò significa che gli uni possono essere costruiti tracciando soltanto rette e cerchi, che altri richiedono invece per la loro costruzione l'uso di almeno qualche sezione conica e che i rimanenti, infine, abbisognano di qualche altra linea più composta. Mi stupisce però che essi, oltre a ciò, non abbiano distinto in diversi gradi queste linee più composte e non capisco perché le abbiano chiamate Meccaniche piuttosto che Geometriche. (ibidem, p. 559)
Descartes dunque critica i Greci per non essere riusciti né a generalizzare i loro metodi di costruzione, né a sottoporli a regole razionali o a una classificazione metodica. Dal suo punto di vista, i Greci seguirono un approccio piuttosto casuale, facendo tentativi di utilizzare la spirale e la quadratrice (curve che oggi chiamiamo trascendenti poiché non possono essere espresse con un'equazione algebrica) come curve da costruzione e, al tempo stesso, senza riuscire a generalizzare l'uso di riga e compasso.
Ci potremmo aspettare che Descartes generalizzi semplicemente sulla base dell'equazione algebrica. Ma, all'inizio del Libro II, invece di fare ricorso alle equazioni, egli fa uso di macchine per tracciare le curve. Infatti concepisce il suo progetto non solo come esplorazione della nuova algebra posta al servizio della ricerca di soluzioni ai problemi geometrici, ma anche, e principalmente, come costruzione geometrica delle radici delle equazioni algebriche, cioè la determinazione di segmenti sulla base di una configurazione data di altri segmenti. Inoltre, come sa molto bene, se la costruzione per punti dei luoghi che ha esposto nel Libro I può apparire come un buon metodo per generare curve sempre più complesse a partire da relazioni razionali fra segmenti, essa non è soddisfacente per generare curve da usare come mezzi da costruzione. La costruzione per punti iterata indefinitamente non garantisce l'esistenza di tutti i punti di intersezione richiesti per le curve che vengono usate come mezzi di costruzione; in questo caso sono richieste condizioni più forti di continuità.
Possiamo confrontare la classificazione dei luoghi che si trova alla fine del Libro I, che sembra più algebrica, con la classificazione dei luoghi, secondo il loro genere, dell'inizio del Libro II (il cui scopo è quello di rendere chiara la prima), che coinvolge strumenti per tracciare curve. Quella posta al termine del Libro I discende da una precedente classificazione dei problemi: quando sono date in posizione tre o quattro linee, i punti richiesti possono essere trovati con riga e compasso; quando le linee sono cinque, sei, sette od otto, i punti possono essere trovati per mezzo di una curva del livello superiore immediatamente successivo, quello che include le sezioni coniche; e quando ve ne sono nove, dieci, undici o dodici, la curva richiesta sarà di un livello ancora più alto. Che cosa dovrebbe includere questo livello?
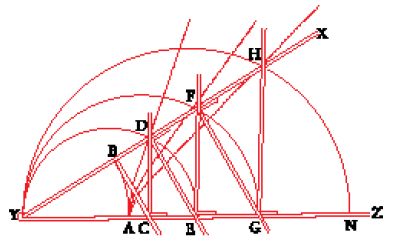
La definizione cartesiana di genere si trova nel bel mezzo della discussione su due macchine per tracciare curve, nelle prime pagine del Libro II. Descartes spiega per quale ragione tali macchine siano generalizzazioni accettabili della riga e del compasso, ovvero perché esse possano essere una possibile fonte per le curve da costruzione richieste nei problemi di livello più alto. La prima macchina di cui Descartes tratta (fig. 11) è un sistema di righe collegate che permette di trovare una, due, tre o più medie proporzionali tra due segmenti dati. Siamo di fronte, ovviamente, a una serie di problemi ordinati. Quando la macchina viene aperta, cioè la riga YX viene spostata verso l'alto, traccia le curve AD, AF, AH e così via, le quali vengono poi utilizzate come curve da costruzione, poiché le loro intersezioni con i cerchi determinano i segmenti cercati, le medie proporzionali. Descartes osserva che queste curve formano una serie di curve algebriche di complessità crescente, anche se non ricava le loro equazioni; non spiega nemmeno le relazioni tra questa serie di problemi e quelli riuniti nel problema di Pappo. Egli non può basarsi solamente sulla sua macchina traccia-linee per generare una serie completa di problemi e curve da costruzione; la serie che viene generata con questo mezzo è troppo specifica. Le sue righe incernierate, per esempio, non producono il frutto del suo metodo che più gli interessa mostrare, la 'parabola cartesiana', una curva che in effetti non è una parabola ma una cubica.
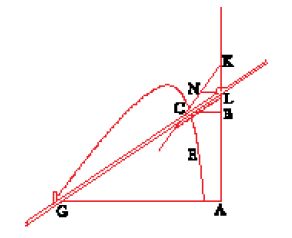
Egli traccia la sua 'parabola' usando un altro meccanismo (fig. 13), che genera curve nuove e più complesse, sfruttando il movimento di curve più semplici. Una riga GL è incernierata in L al dispositivo NKL, che può essere mosso lungo l'asse verticale mantenendo la direzione di KN costante; mentre L scivola su o giù lungo l'asse verticale, GL ruota attorno a G, e la linea KN si muove verso il basso rimanendo parallela a sé stessa. L'intersezione della linea KNC con GL traccia una curva GCE. Quando la linea KN è una retta, GCE è un'iperbole, della quale Descartes ricava l'equazione. Quando KN è un cerchio GCE è una concoide; quando KN è un'iperbole, GCE è la parabola cartesiana, della quale ricava l'equazione. Ci troviamo di fronte un'altra volta a una serie di curve da costruzione e, ancor di più, a una serie abbastanza specifica. Descartes non può assicurare che tutte le curve necessarie per tracciare i luoghi del problema di Pappo, e nemmeno i luoghi stessi, possano essere ottenute con questi meccanismi. Infatti, nel seguito del Libro II, nel secondo caso del problema delle cinque linee, Descartes descrive una curva che non è in grado di tracciare con un movimento continuo. In definitiva, la costruzione per punti del luogo di Pappo non fornisce punti sufficienti per poter essere sicuri che quelle curve siano curve da costruzione; i marchingegni traccia-linee garantiscono la continuità, ma producono serie troppo specifiche e non completamente comprensibili in maniera algebrica; e comunque, sebbene Descartes fosse convinto che tutte le curve algebriche potessero essere descritte come luoghi pappiani, le cose non stanno affatto così.
Inoltre non tutte le procedure per tracciare curve sono accettabili secondo Descartes, che distingue fra curve 'geometriche' e 'meccaniche': una distinzione che equivale a quella moderna fra curve algebriche e trascendenti. Le prime sono tutte e sole quelle che corrispondono a equazioni algebriche; le altre non sono accettabili in geometria. Anche le curve trascendenti possono però essere tracciate per mezzo di procedure precise e poiché nella sua esposizione afferma che le procedure per tracciare le curve devono integrare i metodi algebrici, Descartes deve fornire un criterio per distinguere tra i due tipi di curve. All'inizio del Libro II, non ammette tra le curve geometriche la spirale e la quadratrice (due curve trascendenti), affermando che appartengono alla meccanica e non alla geometria: "Le immaginiamo infatti descritte da due movimenti separati non aventi tra loro nessun rapporto misurabile esattamente" (ibidem, pp. 563-564).
I movimenti per disegnare le curve accettabili da Descartes devono essere tali che il punto tracciato dalla curva sia l'intersezione di due linee (algebriche) rette o curve in movimento, e i movimenti di queste linee devono essere continui e strettamente collegati in base a un movimento iniziale. Che cosa si intenda esattamente per moto continuo e stretta coordinazione non viene mai veramente spiegato nella Géométrie. In definitiva, la separazione posta da Descartes fra curve algebriche e trascendenti (oltre al fatto che egli ritenga che per queste ultime la coordinazione delle linee che le tracciano non sia stretta), si basa sulla convinzione che il 'retto' e il 'curvo' non abbiano fra loro un rapporto razionale. Tale convinzione si fonda sull'applicazione del suo metodo riduzionista alla geometria: nell''ordine della ragione', tutto viene costruito tramite la concatenazione di segmenti.
Per quale ragione Descartes non taglia il nodo gordiano e semplicemente definisce le curve nei termini delle loro equazioni algebriche, classificandole in base al grado della loro equazione? Nel Libro II, la definizione più esplicita di genere di una curva non è data in questi termini. Infatti, sebbene la loro definizione coinvolga la nozione di grado algebrico (dimension), i generi sono definiti in termini di coppie di gradi. Tutte le curve accettabili ammettono una misurazione precisa ed esatta e devono avere una relazione definita rispetto a tutti i punti di una retta; questa relazione deve essere espressa in termini di una sola equazione.
Se tale equazione non sale che al rettangolo di due quantità indeterminate, oppure al quadrato di una sola, la curva appartiene al genere primo e più semplice, nel quale sono comprese soltanto il cerchio, la parabola, l'iperbole e l'ellissi. Quando l'equazione sale invece alla terza o alla quarta dimensione di due quantità indeterminate, o di una delle due ‒ qui infatti ne occorrono due per spiegare la relazione di un punto all'altro ‒, la curva appartiene al secondo genere. E quando l'equazione sale fino alla quinta o sesta dimensione, la curva appartiene al terzo genere: e così delle altre all'infinito. (ibidem, pp. 569-570)
Ci sono almeno tre motivi per cui Descartes fonda la sua classificazione delle curve secondo generi definiti in termini di coppie di gradi. Tutti e tre indicano che egli pensava alle curve non come oggetti interessanti di per sé, ma come mezzi di costruzione nella soluzione dei problemi. Inoltre, tutti e tre comportano generalizzazioni malfondate che contraddicono la fede cartesiana nell''ordine della ragione'. Il primo di questi motivi riguarda la seconda macchina traccia-curve, quella che genera curve nuove e più complesse utilizzando il moto di rette e di curve più semplici. Se a tale macchina si dà in pasto una certa curva perché ne generi una più complessa, questa sembra produrre ‒ almeno nei casi studiati da Descartes ‒ non una curva di grado immediatamente successivo, ma una curva di genere immediatamente successivo. Egli ne derivò che ciò avvenisse sempre; ma le cose non stanno così.
Il secondo motivo è che Descartes fa appello a una regola che riduce ogni problema di quarto grado a una cubica e ogni problema di sesto a uno di quinto grado, di modo che non c'è necessità di considerare il problema di grado più elevato come più complesso dell'altro. È probabile che egli pensasse alla 'regola di Ferrari', che permette di ridurre le equazioni di quarto grado a quelle di terzo: ma una tale regola non sussiste per quelle di quinto e di sesto. E, in ogni caso, la regola di Ferrari riguarda i problemi (si tratta di equazioni a una incognita) e non le curve. Il terzo motivo si basa sulla sua esperienza della cubica nota oggi come 'parabola cartesiana'. Se viene usata quale nuova curva da costruzione, essa rende possibile la soluzione di problemi associati a equazioni di quinto e sesto grado, proprio come l'introduzione della parabola come curva da costruzione permette di risolvere problemi associati a equazioni di terzo e quarto grado. Descartes ne derivò che l'introduzione di una singola curva da costruzione di livello superiore rendesse possibile trovare nuove soluzioni che avrebbero potuto essere classificate per genere, ovvero per coppie di gradi.
Dietro tutti questi motivi che lo indussero a fondarsi sul concetto di genere invece che su quello di grado, possiamo vedere la sua tendenza a ricondurre la ricerca sulle curve a uno studio di problemi; una tendenza derivante dal principio che guida il suo programma: costruire le equazioni mediante la metodologia riduzionista dell''ordine della ragione'. Insomma, questa classificazione rivela che Descartes sta considerando le curve sia dal punto di vista algebrico sia da quello geometrico, cioè come mezzo per costruire geometricamente le radici delle equazioni algebriche. Rivela inoltre che il suo interesse riduzionista non è focalizzato tanto sulla curva in sé, quanto sul collegamento fra i segmenti di retta, nei cui confronti la curva, così come l'equazione algebrica, svolge un ruolo ausiliario. Ciò svela anche l'ambiguità insita nel criterio cartesiano di ammissibilità delle curve, che talvolta si trova formulato in termini di macchine per disegnarle, talvolta in termini di equazioni algebriche. Il suo criterio, infatti, risultava poco chiaro o poco convincente anche per i suoi seguaci, e non molto tempo dopo, quando le curve trascendenti divennero oggetti trattabili dalla matematica, fu abbandonato senza esitazioni.
Lo scopo di Descartes nella Géométrie non è solo quello di classificare i problemi e, rispetto ai problemi, le curve da costruzione, ma anche di fornire un criterio di eleganza ed economia: i problemi devono essere risolti col minor numero possibile di curve da costruzione. È questo l'argomento del Libro III, in cui Descartes tenta di definire un criterio secondo cui una curva possa essere considerata più semplice di un'altra. Il criterio è algebrico: una curva è più semplice se il grado della sua equazione è più basso. Il Libro III è per la maggior parte dedicato alla teoria delle equazioni e delle loro radici; ma non è così puramente algebrico come a prima vista potrebbe sembrare, dato che cerca di trovare costruzioni geometriche standard delle radici delle equazioni che facciano uso della curva da costruzione più semplice possibile. Descartes propone il seguente procedimento: il geometra, di fronte a un problema, deve prima di tutto tradurlo in un'equazione algebrica. Se l'equazione è a una sola incognita, deve verificare se è irriducibile; altrimenti deve ridurla al minimo grado possibile e quindi riscriverla in una forma campione, per determinare quale sia la costruzione standard delle radici per la suddetta forma di equazione. Se l'equazione è in due variabili (come nel caso del problema di Pappo) la soluzione forma un luogo; quindi il geometra costruisce ogni punto che si trova nel luogo scegliendo un valore arbitrario per y e trattando ora l'equazione, che sarà diventata solo in x, secondo il metodo esposto sopra. Descartes afferma che l'equazione di una curva racchiude, in qualche modo, tutte le sue proprietà, ma non spiega come, in generale, queste possano essere ricavate dall'equazione stessa. Fornisce comunque una regola generale: come determinare, sulla base dell'equazione, la normale a una curva; e dato che la normale è la curva perpendicolare alla tangente, come determinare la tangente stessa. Il Libro III, quindi, tratta della riducibilità delle equazioni e della loro forma standard, ma si ferma ben lontano da una completa algebrizzazione della geometria.
Comunque, abbastanza paradossalmente, le idee della Géométrie che ebbero maggiore influenza furono quelle che, da un certo punto di vista, erano più marginali nel progetto cartesiano di organizzazione del campo dei problemi algebrici secondo l''ordine della ragione'. La relazione fra curva ed equazione, così chiara per Fermat, non fu mai centrale per Descartes, il quale considerò l'equazione prima di tutto in relazione ai problemi, e le curve principalmente come curve da costruzione. Perfino il tentativo di fornire una forma standard alle equazioni non si spinse mai fino a proporre l'importante convenzione che gli assi x e y debbano essere scelti perpendicolari fra loro. L'aver enunciato il metodo della radice doppia per la determinazione delle normali (e quindi delle tangenti) alle curve non sembra averlo portato così avanti in queste speculazioni, che condurranno invece Leibniz, quarant'anni più tardi, all'invenzione del calcolo infinitesimale. La comprensione della relazione fra le radici e la forma di un'equazione dovette attendere molte generazioni prima di portare all'algebra astratta, tuttavia il libro di Descartes cambiò per sempre il corso della geometria e della matematica occidentali.
I commenti alla 'Géométrie'
L'esposizione dei risultati raggiunti che Descartes fa nella Géométrie non è certo semplice e i matematici suoi contemporanei la trovarono assai difficile da leggere. Inoltre, come abbiamo già spiegato, l'idea centrale del libro è piuttosto peculiare. Ci vollero un paio di generazioni prima che le sue implicazioni matematiche fossero assimilate. I commenti a questo testo ebbero dunque un ruolo molto rilevante: particolarmente importanti furono le traduzioni latine, ampiamente commentate, pubblicate da Frans van Schooten nel 1649, 1659-1661, 1683 e 1695, che resero l'opera disponibile in quella che all'epoca era la lingua universale degli uomini di scienza e di cultura, chiarendo al tempo stesso molti punti lasciati oscuri da Descartes. Nella seconda edizione, per esempio, il testo cartesiano occupa soltanto le prime cento pagine mentre le rimanenti, almeno novecento, sono di commento. La Géométrie fu recepita da van Schooten in maniera piuttosto conservativa, nel senso che questi la intese come un progetto di ricerca mirato alla costruzione delle equazioni algebriche che rappresentavano problemi geometrici. Nelle edizioni successive aggiunse nuove costruzioni, problemi, luoghi e dimostrazioni; analizzò in maniera più dettagliata i vari casi delle equazioni di secondo grado in due variabili e le soluzioni grafiche delle equazioni di terzo e quarto grado. In queste stesse edizioni erano presenti anche le Notae breves di Florimond de Beaune, il cui modo di affrontare le equazioni di secondo grado in due variabili era più vicino a quello di Fermat. Vanno ricordati anche il Mesolabum di René-François de Sluse e gli Elementa curvarum linearum di Jan de Witt. La prima edizione del Mesolabum (1659) conteneva costruzioni delle equazioni di terzo e quarto grado attraverso la conbinazione di varie sezioni coniche; questi metodi vennero illustrati più estesamente nella seconda edizione (1668). Il libro ebbe una notevole influenza su Blaise Pascal, Christiaan Huygens e Philippe de La Hire, i cui Nouveaux éléments (1679) possono essere considerati il primo manuale sulla costruzione di equazioni di grado arbitrario. De Witt compose nel 1646 gli Elementa curvarum linearum, considerati il primo manuale sulla geometria analitica, ma la sua maniera di affrontare la questione assomiglia più a quella di Fermat che non a quella di Descartes, dato che inizia trattando le equazioni e non i luoghi o le curve. De Witt afferma esplicitamente che un'equazione di primo grado rappresenta una retta (sottolineiamo l'importanza che ciò riveste per il trattamento sistematico del soggetto), arriva inoltre molto vicino all'idea della caratteristica dell'equazione quadratica generale, in quanto deriva le proprietà delle coniche geometricamente e, successivamente, dimostra in maniera analitica che le equazioni di secondo grado rappresentano curve con tali proprietà.
Nello stesso tempo, in Inghilterra, John Wallis perseguì l'aritmetizzazione della geometria suggerita dal libro di Descartes piegandola però verso i suoi scopi. Mentre l'obiettivo di quest'ultimo era di porre l'algebra al servizio delle costruzioni geometriche, quello di Wallis era di esprimere le proprietà delle curve algebricamente, per studiarle attraverso la loro equazione algebrica. Il suo Tractatus de sectionibus conicis (1655) rappresenta la prima esposizione algebrica sistematica delle sezioni coniche data alle stampe: l'opera dapprima definisce le sezioni coniche in maniera puramente analitica ‒ come casi delle equazioni di secondo grado ‒ e quindi, viceversa, dimostra che le curve definite tramite queste equazioni sono proprio le sezioni coniche.
L'invenzione cartesiana della geometria analitica, in teoria, aprì le porte alla definizione, allo studio e alla classificazione di un'intera nuova serie di curve algebriche, soprattutto dopo che venne stabilito uno schema di coordinate nel piano con gli assi ortogonali e con coordinate negative. Ciò permise, da una parte, la determinazione dell'equazione di una qualsiasi curva tracciata o costruita per punti tramite una proprietà ben definita; dall'altra, la rappresentazione grafica di una curva a partire dalla sua equazione. Con l'opera di Leibniz e dei Bernoulli, grazie al perfezionamento della notazione e all'introduzione delle equazioni differenziali e delle serie infinite, si aprì la strada allo studio delle curve trascendenti. Questo fertile terreno non fu sfruttato appieno fino al XVIII sec., quando Leonhard Euler sviluppò una teoria generale delle funzioni. I metodi cartesiani, e quelli contenuti nei commenti alla Géométrie, furono usati in un primo tempo per studiare vecchie curve piuttosto che per inventarne di nuove; l'unica curva, all'interno della Géométrie, che effettivamente rompe con la tradizione precedente è la parabola cartesiana. Le nuove curve che appaiono nelle opere, per esempio, di Newton e di Leibniz sono di solito introdotte per mezzo di strumenti geometrici o meccanici e non saranno prese in considerazione nella geometria analitica fino ai tempi di Euler.
Bibliografia
Belgioioso 1990: Descartes. Il metodo e i saggi, a cura di Giulia Belgioioso [et al.], Roma, Istituto della Enciclopedia Italiana, 1990, 2 v.
Bos 1981: Bos, Henk J.M., On the representation of curves in Descartes' Géométrie, "Archive for history of exact sciences", 24, 1981, pp. 295-338.
‒ 1984: Bos, Henk J.M., Arguments on motivation in the rise and decline of a mathematical theory the 'Construction of equations', 1637-ca. 1750, "Archive for history of exact sciences", 30, 1984, pp. 331-380.
‒ 1990: Bos, Henk J.M., The structure of Descartes' Géométrie, in: Descartes. Il metodo e i saggi, a cura di Giulia Belgioioso [et al.], Roma, Istituto della Enciclopedia Italiana, 1990, 2 v.; v. II, pp. 349-369.
‒ 2001: Bos, Henk J.M., Redefining geometrical exactness. Descartes' transformation of the early modern concept of construction, New York, Springer, 2001.
Boyer 1956: Boyer, Carl B., History of analytic geometry, New York, Scripta Mathematica, 1956.
‒ 1985: Boyer, Carl B., A history of mathematics, Princeton (N.J.), Princeton University Press, 1985 (1. ed.: New York, Wiley, 1968).
Galluzzi 1977: Galluzzi, Paolo, Galileo contro Copernico, "Annali dell'Istituto e Museo di storia della scienza di Firenze", 2, 1977, pp. 87-148.
Giusti 1990: Giusti, Enrico, Numeri, e grandezze e 'Géométrie', in: Descartes. Il metodo e i saggi, a cura di Giulia Belgioioso [et al.], Roma, Istituto della Enciclopedia Italiana, 1990, 3 v.; v. II, pp. 419-439.
Grosholz 1991: Grosholz, Emily, Cartesian method and the problem of reduction, Oxford, Clarendon, 1991.
Lachterman 1989: Lachterman, David R., The ethics of geometry. A genealogy of modernity, New York, Routledge, 1989.
Lenoir 1979: Lenoir, Timothy, Descartes and the geometrization of thought. The methodological background of Descartes' 'Géométrie', "Historia mathematica", 6, 1979, pp. 355-379.
Mancosu 1996: Mancosu, Paolo, Philosophy of mathematics and mathematical practice in the seventeenth century, New York, Oxford University Press, 1996.
Molland 1976: Molland, George, Shifting the foundations. Descartes' transformation of ancient geometry, "Historia mathematica", 3, 1976, pp. 21-49.
Vuillemin 1960: Vuillemin, Jules, Mathématiques et métaphysique chez Descartes, Paris, PUF, 1960.
© Istituto della Enciclopedia Italiana - Riproduzione riservata