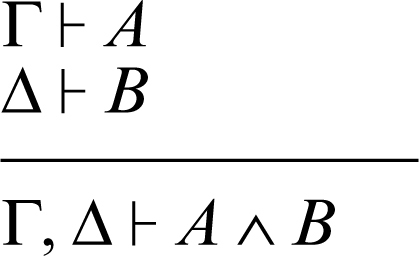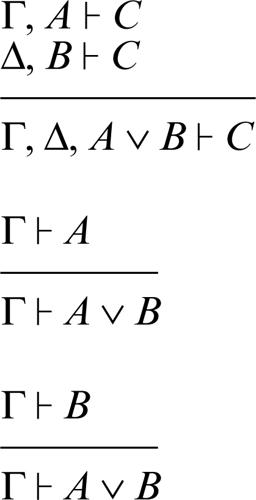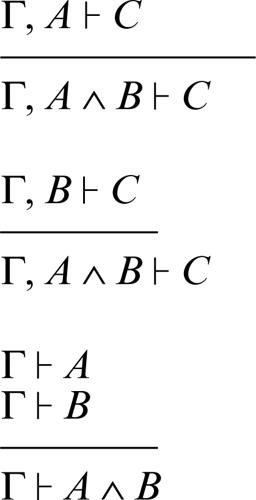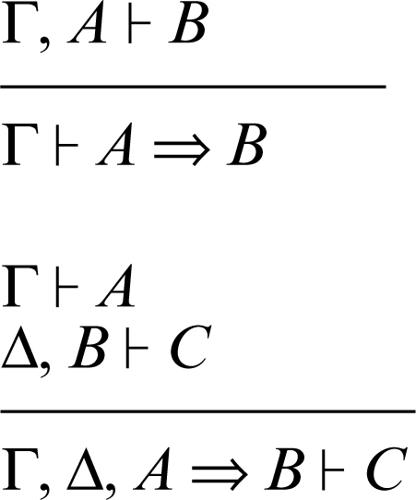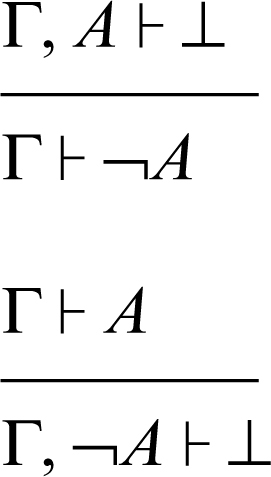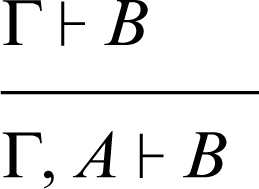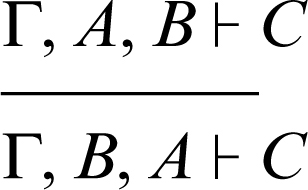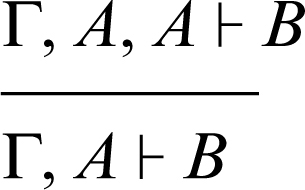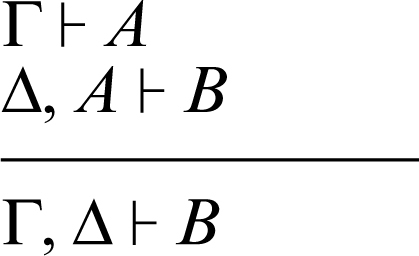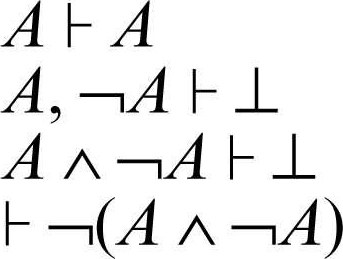Logica intuizionista

logica intuizionista

logica intuizionista teoria logica nata nel contesto dell’→ intuizionismo, filosofia della matematica elaborata da L.E.J. Brouwer nel 1907. Secondo Brouwer in matematica sono da considerare realmente esistenti solo gli oggetti di cui è possibile fornire una costruzione mentale e quindi, per sostenere la validità di una proposizione A, bisogna esibire la costruzione di un oggetto che soddisfi la proposizione A. Tale impostazione ha profonde conseguenze in logica, soprattutto a causa della negazione del principio del → terzo escluso, punto cardine della logica classica. Il principio del terzo escluso è in contraddizione con la logica intuizionista in quanto postula la validità di una delle due proposizioni (A o ￢A) senza prevedere una costruzione che dimostri l’una o l’altra. Si consideri per esempio la seguente affermazione indicata con la lettera G e nota sotto il nome di congettura di Goldbach, G: «Ogni numero n pari e maggiore di due può essere scritto come somma di due numeri primi anche uguali fra loro». Sebbene la maggior parte della comunità matematica ritenga che la proposizione G sia vera, essa non è mai stata dimostrata né confutata (cioè non è stata dimostrata neanche la sua negazione ￢G). Tuttavia, secondo la concezione della logica classica, è possibile affermare che o la proposizione G è vera o è vera la sua negazione ￢G. Ciò viene messo in discussione dalla logica intuizionista in quanto, non avendo un metodo generale per decidere la validità della proposizione G per ogni numero naturale n, è impossibile affermare che «G è vera oppure ￢G è vera» poiché nessuna delle due è stata dimostrata. Secondo Brouwer, il principio del terzo escluso è ricavato dall’osservazione di proprietà in un numero finito di casi e impropriamente esteso a proprietà che valgono per gli insiemi infiniti. Per esempio, l’affermazione P: «ogni numero naturale minore di 5 è dispari» riguarda l’insieme finito di numeri {1, 2, 3, 4} e può essere solo vera o falsa; provando a verificarla per i quattro numeri precedenti ci si rende conto che P è falsa perché 4 è un numero minore di 5 ed è pari. Questo procedimento non può però essere esteso a proposizioni che riguardano infiniti numeri come la proposizione G perchè occorrerebbe effettuare infinite verifiche; perciò non è possibile affermare nulla sulla verità di G o di ￢G a meno che non si abbia un metodo generale che le dimostri per ogni numero n.

La logica intuizionista pone il problema della costruibilità anche in relazione alle dimostrazioni matematiche, le quali devono essere pensate come una serie di passaggi volti a costruire un oggetto matematico che soddisfi la proprietà che si vuole dimostrare. Non è invece accettabile un dimostrazione che assicuri, su basi logiche, l’esistenza di un oggetto senza fornire una procedura, seppur teorica, per costruirlo. Per il loro carattere non costruttivo, anche le → dimostrazioni per assurdo, poiché si basano sul principio del terzo escluso, sono rifiutate dalla logica intuizionista. Anche se, per quanto detto, la logica intuizionista appare restrittiva, non accettando per esempio tutti i risultati raggiunti con le dimostrazioni per assurdo, tuttavia la concezione intuizionista delle dimostrazioni (procedimenti costruttivi che forniscono una risposta sulla verità o falsità di un certo enunciato A in un numero finito di passi) ha avuto il merito di creare un terreno fertile per la teoria della → ricorsività e della → calcolabilità. Per questo motivo la logica intuizionista è stata recuperata nelle applicazioni della logica all’informatica teorica. In particolare, grazie all’isomorfismo di → Curry-Howard, è possibile affermare che ogni dimostrazione della logica intuizionista corrisponde a un programma.

Come nel linguaggio degli enunciati e nel linguaggio dei predicati è possibile realizzare dei sistemi formali per la logica classica, allo stesso modo i principi della logica intuizionista possono essere formalizzati attraverso un linguaggio e un calcolo logico, in cui è rappresentata la deduzione.

Un calcolo che si presta particolarmente alla formalizzazione della logica intuizionista è il calcolo dei sequenti, introdotto da G. Gentzen negli anni Trenta del secolo scorso.

Qui di seguito è riportato un esempio di calcolo dei sequenti per la logica intuizionista (indicato con l’abbreviazione LJ) sviluppato su un linguaggio enunciativo. I simboli del linguaggio sono i seguenti:

• le lettere A, B, C, … per indicare gli enunciati atomici cioè non ulteriormente scomponibili (→ formula atomica);

• i simboli dei connettivi: ￢ (negazione), ∧ (congiunzione), ∨ (disgiunzione), ⇒ (implicazione), ⇔ (doppia implicazione);

• le costanti logiche: ⊺ per indicare un predicato sempre vero e ⊥ per indicare un predicato sempre falso;

• le parentesi.

Con i simboli sopra elencati si costruiscono le formule ben formate esclusivamente secondo le seguenti regole:

• ogni enunciato atomico è una formula ben formata;

• le costanti logiche ⊺ e ⊥ sono formule ben formate;

• se P e Q sono formule ben formate, allora anche ￢P, P ∧ Q, P ∨ Q, P ⇒ Q, P ⇔ Q sono formule ben formate.

Una volta stabilito il linguaggio, un sequente della logica intuizionista è una espressione del tipo A₁, A₂, …, A_n ⊢ B, in cui B è una formula ben formata mentre A₁, A₂, …, A_n è una lista di formule ben formate. Spesso per indicare la lista di formule si utilizzano lettere dell’alfabeto greco: per esempio si può rappresentare la lista A₁, A₂, …, A_n con la lettera Γ e il sequente diventa Γ ⊢ B. L’interpretazione del sequente è: «dalle premesse Γ segue la conclusione B».

Nel calcolo dei sequenti vengono rappresentate formalmente le dimostrazioni della logica intuizionista nel modo seguente: si parte da uno o più assiomi e si arriva, applicando le regole di deduzione, alla conclusione. Per esemplificare come vengono schematizzate le regole di deduzione nel calcolo dei sequenti, si riporta di seguito la regola di introduzione del connettivo ∧ (congiunzione):

dove la linea orizzontale sta a significare che dai due sequenti Γ ⊢ A e Δ ⊢ B (premesse) si deduce logicamente il sequente Γ, Δ ⊢ A ∧ B (conclusione).

Nel calcolo dei sequenti intuizionista gli assiomi sono:

• identità: A ⊢ A;

• definizione della costante ⊥: ⊥ ⊢ A (da una premessa falsa deriva qualsiasi conclusione);

• definizione della costante ⊺: Γ ⊢ ⊺ (il predicato sempre vero è conclusione di qualsiasi premessa).

Le regole di deduzione sono:

a) regole logiche:

disgiunzione

congiunzione

implicazione

negazione

b) regole strutturali

indebolimento

scambio

contrazione

c) regola del taglio

Il calcolo dei sequenti può essere utilizzato anche per la logica classica (viene indicato con l’abbreviazione LK): in tal caso però il sequente ha la forma Γ ⊢ Δ in cui anche Δ è una lista di formule. Quindi, al contrario dei sequenti intuizionisti, i sequenti della logica classica possono avere più di una formula a destra del simbolo ⊢. Questa differenza è essenziale perché permette di dimostrare, nel calcolo dei sequenti della logica classica, il principio del terzo escluso espresso dalla formula A ∨ ¬A. Di seguito si riporta la deduzione di tale formula nel calcolo dei sequenti della logica classica:

L’ultimo sequente scritto rappresenta il principio del terzo escluso. Si osservi però che questa deduzione non rispetta le regole del calcolo dei sequenti intuizionista. Infatti dopo l’applicazione della regola sulla negazione si ottiene un sequente con due formule a destra. Bisogna tuttavia notare che il principio di non contraddizione, che è alla base della logica classica ed è espresso dalla formula ¬(A ∧ ¬A), continua invece a valere anche in logica intuizionista come si evince dalla seguente deduzione: