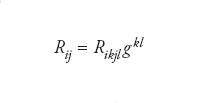Tensore di Ricci

tensore di Ricci

Sia M una varietà dotata di una metrica riemanniana. Indichiamo rispettivamente con g_ij e con R_ijkl le espressioni locali della metrica riemanniana e delle componenti del tensore di curvatura. A partire da quest’ultimo, si definisce un altro tensore, detto di Ricci, le cui componenti sono date nel modo seguente:

Si ricorda che per alleggerire le notazioni, si applica l’usuale convenzione secondo la quale un indice ripetuto in ogni addendo (in questo caso ‘r’) sostituisce una sommatoria (∑_r). I coefficienti g^kl sono gli elementi della matrice inversa di g_kl. È degno di nota il fatto che i tensori R_ij e g_ij siano esattamente dello stesso tipo: sono entrambi simmetrici, cioè non variano scambiando tra loro i e j. Il tensore di Ricci fornisce un modo per dare una misura di quanto la geometria determinata da una varietà riemanniana differisca dalla geometria dello spazio euclideo ordinario. Infatti, su una varietà riemanniana esistono delle coordinate locali rispetto alle quali i coefficienti g_ij della metrica possono essere approssimati da quelli della metrica euclidea a meno di termini quadratici. Rispetto a tali coordinate la forma di volume di M si esprime in termini della forma di volume euclideo a meno di termini che coinvolgono il tensore di Ricci.

→ Geometria differenziale