Il caso di orizzontale, verticale e obliquo
Orizzontale, verticale e obliquo sono parole ricorrenti nella vita quotidiana, quando ci orientiamo o diamo indicazioni: generalmente dormiamo in posizione orizzontale, facciamo cruciverba scegliendo fra verticali e orizzontali, raddrizziamo quadri appesi in modo obliquo. Sono, inoltre, diffuse in campi specifici del sapere, come in geografia, e − in modo improprio – in geometria, soprattutto nei testi scolastici. L’uso di una parola nel quotidiano non comporta, infatti, automaticamente, che lo stesso uso sia idoneo a un contesto settoriale, perché contesti diversi sono regolati da scelte, proprietà e criteri almeno in parte diversi. Per capire a fondo la matematica è necessario rendersi conto delle sue specificità, così da poterla osservare con il giusto sguardo.
Che cosa dicono i dizionari?
Nel Gradit (Grande dizionario italiano dell’uso) di Tullio De Mauro, una marca d’uso indica per ogni accezione dei lemmi la caratterizzazione relativa alla frequenza: ad esempio, si hanno parole FO, appartenenti al lessico fondamentale, AU (di alto uso), AD (di alta disponibilità), meno ricorrenti ma note al parlante medio, e categorie più specifiche, come le parole LE, di uso letterario. Vi è anche la categoria TS: il lessico tecnico-specialistico (almeno quello più stabilmente entrato nell’uso), più o meno circoscritto all’ambito di riferimento. Osservare i significati dei termini TS permette di cogliere intersezioni o divergenze fra lingua comune e specificità disciplinari.
Nel caso in esame, gli aggettivi verticale (link), orizzontale (link) e obliquo (link) sono marcati come TS in riferimento al lessico specialistico della geometria, ma verticale è anche parola AU, di alto uso, e orizzontale è anche AD, di alta disponibilità; obliquo è solo TS, ma sappiamo bene come anche questo aggettivo sia usato nel quotidiano. Un quotidiano fatto di oggetti concreti, posizionati l’uno rispetto all’altro in modo relativo. Dunque sono davvero parole della geometria? O, nel tempo, per prassi comunicativa e didattica si è consolidata l’abitudine di presentare la geometria ricorrendo a queste parole, che però non le sono proprie e non permettono di comprenderne l’essenza?
I tre aggettivi nei manuali: una convenzione vincolante
Chi, tra i lettori, non ricorda − nella propria esperienza scolastica di geometria – casi d’uso come quelli presentati qui di seguito?
Tre rette o una sola?
In quasi tutti i testi di scuola primaria si parla di retta mostrandone tre posizioni diverse rispetto al lettore: orizzontale, verticale e obliqua. Tale classificazione viene così percepita dall’allievo come una distinzione che caratterizza la retta stessa, e non (banalmente, fisicamente e graficamente) la sua rappresentazione sul foglio rispetto al lettore; l’allievo è così indotto erroneamente a pensare che esistano tre tipi distinti di retta, dipendenti dalla posizione che essa assume. A tal proposito, uno studente di V superiore (M.), alla domanda «Immagina di spiegare a un tuo compagno che cos’è la retta in matematica. Tu che cosa gli diresti?», risponde in questo modo:
M.: La retta in matematica è questa 
questa  o questa
o questa 
riproponendo tre volte lo stesso ente geometrico, una retta, solo disposto in posizioni diverse rispetto al bordo del foglio, fornendo così una risposta impropria dal punto di vista matematico.
Il lato obliquo del trapezio
Una convenzione accettata da anni da quasi tutto il mondo della scuola, e per questo presente in tutti i libri di testo, è quella di chiamare il lato del trapezio indicato nel seguente disegno “lato obliquo”:
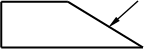
Questa scelta è costruttiva per l’apprendimento o è fonte di ostacoli didattici? A nostro parere, tale scelta linguistica genera misconcezioni, poiché vincola la posizione da far assumere all’oggetto, come se fosse un proprietà di esso. La conferma al fatto che l’essere obliquo non è una proprietà è data dalla seguente figura, che rappresenta lo stesso trapezio, ma disposto in modo diverso rispetto ai margini del foglio: in esso tutti i lati risultano obliqui rispetto al lettore tranne proprio quello che per convenzione è chiamato obliquo.
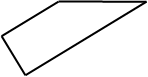
A questo punto, come spesso accade, lo studente potrebbe non riconoscere più il trapezio o per farlo potrebbe doverlo riportare nella posizione da lui considerata standard: con il lato etichettato come obliquo disposto in modo che lo sia effettivamente rispetto al proprio punto di vista. Tale misconcezione è evitabile, in quanto dipende dalla scelta di un termine che dà maggiore risalto alla posizione dell’oggetto, piuttosto che all’essenza dell’oggetto stesso, valorizzando così un sapere esterno al contesto matematico, che può bloccare l’apprendimento concettuale corretto.
L’istituzionalizzazione di una scelta
Durante una sperimentazione in una classe IV di scuola primaria di Mirano (VE) si è presentata la seguente situazione, ampiamente studiata dalla ricerca in didattica della matematica. Dopo aver costruito dei fogli quadrati di carta in cui si erano anche evidenziate le pieghe in corrispondenza delle diagonali, il ricercatore ha disposto il proprio modello di quadrato nella seguente posizione, “inaspettata” rispetto a quella “classica” scelta dai bambini per parlare di quadrato:
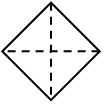
A questa provocazione i bambini hanno obiettato: «Quello che hai in mano tu è un rombo, quello che abbiamo in mano noi è un quadrato» (tenevano il quadrato nel modo stereotipo classico, con due lati paralleli al pavimento). Il ricercatore ha allora sollecitato la discussione domandando: «Perché quello che ho in mano io è un rombo e il vostro è un quadrato?». E bambini: «Perché la maestra ci ha detto che il rombo ha le diagonali orizzontali e verticali, mentre il quadrato ha le diagonali oblique».
Nella logica di ciò che era stato loro insegnato, i bambini avevano ragione. La rappresentazione e l’indicazione verbale che l’insegnante aveva fornito ai propri allievi, in buona fede, allo scopo di aiutarli, risultava in realtà un ostacolo all’apprendimento, dato che fissava l’attenzione solo su una particolare posizione assunta dall’oggetto. Tale posizione risultava intuitiva per gli allievi, essendo percettivamente immediata, ma celava le caratteristiche matematiche del concetto.
Lingua e geometria: l’inadeguatezza dell’uso ricorrente
Insomma, poiché il come si parla di qualcosa influenza il modo stesso di vedere e concepire quella cosa, l’uso di simili parole in ambito geometrico non è senza effetti, in quanto orienta l’attenzione sulla posizione dell’oggetto, invece di dare importanza alla sua essenza. È vero che, come sostengono Stavy e Tirosh (2000),
[…] le linee verticali e orizzontali costituiscono le direzioni fondamentali su cui gli oggetti possono essere orientati in relazione alla gravità. Evidentemente, la percezione delle linee verticali e orizzontali è programmata nel sistema visivo dei mammiferi.
Tuttavia, in geometria risulta fondamentale saper rilevare le caratteristiche “assolute” dell’oggetto matematico, come il parallelismo, la perpendicolarità, la congruenza dei lati o degli angoli ecc., indipendenti dal punto di vista. Lo spazio della geometria euclidea è, in effetti, di tipo isotropo (in cui tutte le direzioni per un punto si equivalgono), a differenza dello spazio anisotropo dell’esperienza fisica (che possiede una direzione privilegiata rappresentata dalla verticale). Soprattutto nella scuola primaria, occorre curare il passaggio dallo spazio anisotropo del bambino, della sua esperienza corporea, allo spazio isotropo della geometria, cercando di mantenere la diversità dei due contesti. Occorre quindi non vincolare l’apprendimento geometrico a prassi didattiche improprie e vincolanti, legate a caratteristiche concrete, dirette e percepibili, importanti nella vita reale, ma di ostacolo in ambito geometrico, nel quale non esistono “direzioni privilegiate”. È per questo che da anni proponiamo un’attenta riflessione linguistica, per cui parole “relative” come verticale, orizzontale e obliquo sono da considerare tabù (come nell’omonimo gioco) quando si parla di proprietà del mondo geometrico.
Riferimenti bibliografici
D’Amore, B., Fandiño Pinilla, M. I., Marazzani, I., & Sbaragli, S. (2019). Le difficoltà di apprendimento in matematica. Bologna: Pitagora.
D’Amore B., Sbaragli S. (2005). Analisi semantica e didattica dell’idea di “misconcezione”. La matematica e la sua didattica, 2, 139-163.
De Mauro, T. (1999). Gradit. Grande dizionario italiano dell’uso. Torino: UTET.
Gallo, E. (1985). Geometria, percezione, linguaggio. L’Educazione matematica, 6(1), 61-104.
Sbaragli, S. (2005). Misconcezioni “inevitabili” e misconcezioni “evitabili”. La matematica e la sua didattica, 1, 57-71.
Sbaragli, S. (2014). Una lettura didattica della metafora degli “occhiali della matematica”. In D’Amore, B., & Sbaragli, S. (2014). Parliamo tanto e spesso di didattica della matematica. Bologna: Pitagora, 49-56.
Stavy, R., & Tirosh, D. (2000). Perché gli studenti fraintendono matematica e scienze? Trento: Erickson.
La prima puntata dedicata dalle autrici all'italmatica:
Italmatica: l’unione di due mondi. Riflessioni tra teoria e didattica – 1 (link)
Immagine: Allegoria della geometria
Crediti immagine: Laurent de La Hyre [Public domain]
© Istituto della Enciclopedia Italiana - Riproduzione riservata
