Circuitazione
Enciclopedia on line
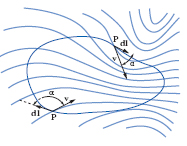
Nell’analisi vettoriale, se v (P) è il vettore di un campo vettoriale e l è una linea assegnata nella regione sede del campo, P il suo generico punto, dl lo spostamento elementare di P, si chiama c. (o circolazione) elementare di v il prodotto scalare v ∙ dl = v dl cos α e c. di v relativa alla l l’integrale di linea (v. fig.) ∫l v ∙ dl; talvolta, specialmente se l è una linea chiusa, si usa per l’integrale il simbolo ∮ v ∙ dl. Se si cambia il verso di percorrenza su l, la c. conserva il suo valore assoluto, ma cambia di segno; se, in particolare, il campo è conservativo, la c. dà la differenza di potenziale relativa agli estremi di l, se questa non è chiusa, ed è nulla se l è chiusa. Si dimostra poi ( teorema della c. o di Stokes ➔ rotore) che la c. di v relativa a una linea chiusa l è uguale al flusso del rotore di v attraverso una qualunque superficie S che abbia l come contorno.
Teorema della c. del campo elettrico La c. di un campo elettrico E relativa a un circuito chiuso l è uguale alla derivata temporale del flusso del campo di induzione magnetica B attraverso una qualunque superficie avente la linea l come bordo. Utilizzando il teorema di Stokes, tale teorema, può essere scritto nella forma differenziale rot E=−∂B/∂t e, come tale, costituisce una delle equazioni fondamentali dell’elettromagnetismo.
Teorema della c. del campo magnetico Nei casi stazionari la c. dell’intensità H di un campo magnetico relativa a una linea chiusa l è uguale alla somma algebrica delle intensità delle correnti concatenate con la linea chiusa stessa. Nei casi non stazionari, quando vari nel tempo il vettore spostamento D, al termine delle correnti si aggiunge la derivata temporale del flusso del vettore D attraverso una qualunque superficie avente la linea l come bordo. Utilizzando il teorema di Stokes, tale teorema può essere scritto nella forma differenziale rot H=J+∂D/∂t e, come tale, costituisce una delle equazioni fondamentali dell’elettromagnetismo.
© Istituto della Enciclopedia Italiana - Riproduzione riservata