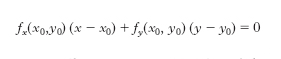Curva

Matematica

Generalità

Nel linguaggio matematico, sinonimo di linea, intendendosi quindi anche la retta come una particolare curva. Una definizione di c. valida in ogni caso non è possibile per il fatto che non sono ben precisati i requisiti che deve avere un ente per potersi chiamare curva. Le antiche concezioni della c., come serie di punti-monadi (Pitagora), o lunghezza senza larghezza (Euclide), o traiettoria di un punto mobile, o termine di una superficie, sono evidentemente superate o non abbastanza precise. Anche una definizione analitica, che colleghi il concetto di c. al concetto di funzione, non è esente da inconvenienti. Nella matematica moderna si parla perciò non di c. in senso assoluto, ma dell’uno o dell’altro tipo di c. (c. continua, c. di Jordan, c. analitica e simili) essendo ciascun tipo rigorosamente definito. Precisando matematicamente il particolare tipo di c., è però possibile che vengano meno una o più proprietà che, secondo l’intuizione, dovrebbero essere peculiari di una curva. Così, la c. di Jordan può non possedere alcune delle proprietà intuitive di una c. (per es., l’esistenza di una tangente in tutti i punti), pur conservando sempre il carattere di un ente a una dimensione; invece la c. di Peano non ha neppure questo carattere, poiché comprende i punti di un intero quadrato. A questa distinzione si affianca una classificazione delle c. in base ad altre proprietà, di natura diversa (c. algebriche, trascendenti, piane, sghembe ecc.).

Molte c. di tipo particolare sono usualmente denotate mediante il nome del primo che le considerò (per es., c. di Lamé), ovvero mediante un nome che indichi una loro proprietà o il modo di generarle ( c. podarie), ovvero ricordi la loro forma (per es., la c. cardioide). Ricordiamo infine che, nell’ambito della topologia, la nozione di c. viene naturalmente messa in relazione alle proprietà di continuità dello spazio ambiente e le relative proprietà geometriche vengono adeguatamente descritte mediante la considerazione di certi caratteri tipici, come quelli di annodamento di una c. o allacciamento di una c. con un’altra c. (➔ nodo; treccia).

Rappresentazione analitica

Una c. si può rappresentare analiticamente in varie maniere qualora si introduca un sistema di coordinate nello spazio in cui essa è immersa. La c. sarà allora rappresentata da equazioni soddisfatte dalle coordinate di tutti e soli i punti della c. stessa. Si ha per es., nel caso delle c. piane, l’equazione cartesiana f (x, y)=0, la quale si può pensare risolta rispetto a una delle due variabili: y=y (x) o x=x (y); l’equazione polare f (r, ϑ)=0, o più in generale l’equazione, in un sistema qualunque di coordinate, f (u, v)=0; ovvero le equazioni parametriche x=x (t), y=y (t) che danno x, y in funzione di un parametro t (variabile in un certo intervallo), o anche, più in generale, f_i (x, y, t₁, ..., t_n)=0 (i=1, ..., n+1), che danno n + 1 legami tra x, y e n parametri t₁, ..., t_n: si passa dalle equazioni parametriche all’equazione cartesiana eliminando il parametro o i parametri tra le ultime equazioni scritte (si osservi tuttavia che tale eliminazione non è necessaria per la conoscenza della c. e, spesso, non è opportuna per la complicazione dei calcoli che può richiedere). Le c. dello spazio ordinario si rappresentano mediante due equazioni cartesiane f (x, y, z)=0, g (x, y, z)=0, eventualmente risolte rispetto a due delle variabili: x=x (z), y=y (z); ovvero mediante n+2 equazioni parametriche contenenti n parametri. Analogamente, negli iperspazi, con r−1 equazioni nelle r coordinate, ovvero con n+r−1 equazioni nelle coordinate e in n parametri. Le funzioni che uguagliate a zero rappresentano la c. o che appaiono nelle equazioni parametriche sono di norma soggette a opportune condizioni di regolarità, come la continuità e la derivabilità.

C. piane

Tale è ogni c. contenuta in un piano. Sia f (x, y)=0, ovvero y=y (x), l’equazione di una c. piana, in coordinate cartesiane ortogonali, con f (x, y) ovvero y (x) funzioni continue e derivabili quante volte occorra. Tra le nozioni e le proprietà di natura differenziale di una c. piana ricordiamo le seguenti: ascissa curvilinea (➔ coordinate), lunghezza del tratto di c. compreso tra un punto generico della c. e un suo punto prefissato; l’uso dell’ ascissa curvilinea facilita lo studio differenziale della c. ed è connesso in particolare con il problema della rettificazione della c. stessa. Tangente in un punto P₀ della c. è il limite della retta P₀P, al tendere del punto P a P₀ lungo la curva; essa ha equazione

dove f_x e f_y sono le derivate parziali della funzione f, ovvero y−y₀=y′ (x₀) (x−x₀) dove y^′ è la derivata della funzione y (x). Normale in P₀ è la retta perpendicolare per P₀ alla tangente, di equazione

Cerchio osculatore è il limite del circolo per P₀, P, Q, quando P, Q tendono a P₀ lungo la c.; raggio di curvatura e curvatura sono il suo raggio e l’inverso di esso. Parabola osculatrice d’ordine n è la c. rappresentata dai primi n+1 termini dello sviluppo di Taylor della y=y (x); essa ha contatto (n+1)-punto con la curva. Flesso è un punto O in cui la tangente ha contatto tripunto: si ha qui y″, (x₀)=0, ma in tal caso si può avere anche un punto di ondulazione (contatto quadripunto) o un flesso di specie superiore (contatto d’ordine maggiore). Asintoto è la retta limite di una tangente il cui punto di contatto tenda all’infinito (purché tale retta limite sia distinta dalla retta impropria). Punto singolare è un punto doppio con tangenti reali e coincidenti (➔ cuspide), reali e distinte (➔ nodo), complesse coniugate (➔ isolato, punto). Ramo è ogni parte di c. rappresentabile in forma parametrica con due sviluppi in serie di potenze del parametro.

C. piane algebriche

Tale è ogni c. piana la cui equazione in coordinate x, y proiettive o, in particolare, cartesiane, è del tipo f (x, y)=0 dove f è un polinomio; spesso si usano coordinate omogenee, x₁, x₂, x₃: l’equazione della c. è allora F (x₁, x₂, x₃)=0 con F polinomio omogeneo.

Proprietà proiettive delle c. algebriche sono: ordine è il numero dei punti d’incontro con una retta generica del piano: è uguale al grado del polinomio f (x, y); classe è il numero delle tangenti che si possono condurre alla curva da un punto generico del piano; punto di molteplicità s o s-uplo è un punto tale che la retta generica per esso abbia s delle sue intersezioni con la c. assorbite in quel punto (per es., nodo, cuspide, tacnodo sono punti di molteplicità s=2); tangenti in un punto multiplo, più propriamente tangenti principali, sono quelle particolari rette per il punto che hanno almeno s + 1 delle loro intersezioni con la c. assorbite in quel punto; genere di una c. algebrica piana, dotata solo di d punti doppi nodali o cuspidali e senza altri punti multipli, è il numero intero (mai negativo) p=(n−1) (n−2)/2−d. Esempi di c. algebriche piane sono le rette (ordine 1), le coniche (ordine 2), le cubiche (ordine 3).

C. sghembe (o c. gobbe)

Ogni c. che non giace in un piano, ma nello spazio ordinario o in un iperspazio. Per le c. dello spazio ordinario si considerano le seguenti proprietà differenziali: ascissa curvilinea, come nel caso delle c. piane, è la lunghezza del tratto di c. compreso tra un punto generico della c. e un suo punto prefissato; se si assume come parametro l’ascissa curvilinea, si ha la rappresentazione parametrica x=x (s), y=y (s), z=z (s), che riesce particolarmente agevole per lo studio delle proprietà differenziali. Tangente è, come per le c. piane, il limite della corda. Piano osculatore in P₀ è il limite del piano P₀PQ, quando P, Q tendono a P₀ sulla curva. Normale principale è la perpendicolare alla tangente per P₀ condotta nel piano osculatore. Binormale è la perpendicolare in P₀ al piano osculatore. Piano normale è il piano per P₀ perpendicolare alla tangente. Piano rettificante è il piano perpendicolare alla normale principale condotto per P₀. Triedro principale è quello costituito da tangente, normale principale e binormale. Sfera osculatrice è il limite della sfera per P₀, P, Q, R quando P, Q, R tendono a P₀ lungo la curva. Cerchio osculatore è l’intersezione della sfera osculatrice con il piano osculatore. Flessione o prima curvatura è l’inverso del raggio del cerchio osculatore. Torsione o seconda curvatura, in P₀, è la derivata, rispetto all’ascissa curvilinea, dell’angolo formato dal piano osculatore in P₀ e da un piano osculatore variabile. Flesso, asintoto, punto singolare, ramo si introducono seguendo un procedimento analogo a quello impiegato per le c. piane. Analoghe sono le definizioni negli iperspazi. Esempi di c. sghembe sono l’elica cilindrica, la finestra di Viviani, le quartiche di prima e di seconda specie.

C. sghembe algebriche

Nello spazio ordinario è tale ogni c. sghemba che risulti intersezione (completa o no) di due superfici algebriche. Essa si può sempre ottenere come intersezione completa di, al più, 4 superfici algebriche. Negli iperspazi di dimensione r si ottiene come intersezione di r-1 o più forme algebriche. Sono proprietà delle c. algebriche (nello spazio ordinario): ordine è il numero dei punti d’incontro con un piano generico dello spazio; classe è il numero dei piani tangenti passanti per una retta generica, e coincide col numero delle tangenti incidenti una retta generica; rango è il numero dei piani osculatori passanti per un punto generico.

Vari tipi di curve

1A

2

3

C. algebrica

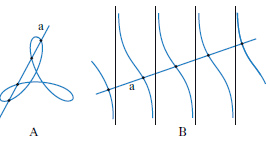
Si può pensare come una varietà algebrica a una dimensione. Per le c. algebriche del piano e dello spazio ordinario vedi sopra (c. piane e c. sghembe). Una c. non algebrica si dice trascendente. Una differenza geometrica fondamentale tra c. algebrica e c. trascendente è quella che, mentre una retta generica a incontra una c. del primo tipo in un numero finito di punti (fig. 1A), essa può incontrare in infiniti punti una c. del secondo tipo (fig. 1B).

C. analitica

C. piana che si rappresenta in coordinate cartesiane uguagliando a zero una funzione analitica in due variabili, ovvero c. rappresentata da y=y (x), essendo y (x) una funzione analitica. C. di Archita È storicamente la prima linea sghemba considerata; fu ideata da Archita nell’intento di risolvere il problema della duplicazione del cubo. È la quartica razionale di prima specie, intersezione di un cilindro e di un cono di rotazione opportunamente scelti: per es., del cilindro di equazione x² + y²=ax e del cono x²+y²+z²=a²x²/b², ove a e b sono costanti positive ed è a > b. C. di Jeřábek Cubica circolare (fig. 2), così costruita: siano A, O, C tre punti allineati, presi nell’ordine, con AO=OC, e sia a la retta per A perpendicolare alla retta AO. Presa una retta r variabile per O, siano D ed E i suoi punti d’incontro con a e con la circonferenza di centro C e raggio CO; sulla r si porti OP uguale in valore e segno a DE: il luogo di P è la c. di Jeřábek. La sua equazione cartesiana, scegliendo gli assi x e y come in figura, è: (x²+y²) (x−d)=2dy² dove d=AO=OC. La c., simmetrica rispetto all’asse y, ha un punto doppio isolato in O e ha la retta y=d come asintoto.

C. di Peano

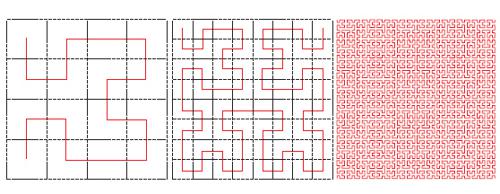
Particolare c. costruita da G. Peano per dimostrare errate alcune conclusioni che sembrano invece evidenti nello studio delle proprietà delle c. e che si sono presentate nella definizione dei loro attributi. È una c. piana rappresentata da due equazioni parametriche x=x (t), y=y (t) dove le x (t), y (t) sono due funzioni continue, sebbene non derivabili in alcun punto, opportunamente definite in modo tale che la c. così rappresentata sia costituita da tutti i punti di un quadrato (interni e sul perimetro). Si dimostra quindi erroneo il concetto di c. continua come di un ente a una dimensione. In fig. 3 sono disegnate tre c. che costituiscono stadi successivi, ad approssimazione crescente, della costruzione delle c. di Peano.

Economia

C. di indifferenza

Rappresentazione grafica delle combinazioni di due beni che danno all’individuo la stessa soddisfazione in termini di benessere (utilità). In tutti i punti di una data c. il livello di soddisfazione è identico, mentre esso è maggiore per ogni c. man mano che ci si sposta sul piano cartesiano dall’origine degli assi verso l’alto. Le c. sono decrescenti perché all’aumento della quantità di un bene si accompagna la diminuzione della quantità dell’altro bene affinché l’individuo abbia la stessa soddisfazione. Le c. sono inoltre convesse verso l’origine degli assi perché, man mano che diminuisce il consumo di un bene (ogni volta di una quantità data), occorrono quantità ogni volta maggiori dell’altro bene per compensare l’individuo, lasciando la sua soddisfazione inalterata. Infatti, un bene, man mano che diviene più scarso, diviene sempre più prezioso per l’individuo (principio dell’utilità marginale decrescente). La pendenza della c. di indifferenza viene misurata attraverso il saggio marginale di sostituzione che rappresenta il rapporto di scambio tra i due beni. Il saggio è decrescente perché riflette la proprietà dell’utilità marginale decrescente. Le c. di indifferenza sono state introdotte nella scienza economica da F.Y. Edgeworth e largamente usate da V. Pareto, che mise in evidenza che mediante esse si potevano raggiungere gli stessi risultati della teoria utilitaristica senza ricorrere però mai alla ipotesi che l’utilità, cioè il piacere, la soddisfazione psichica dell’individuo, fosse misurabile.