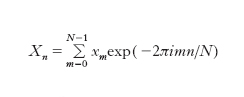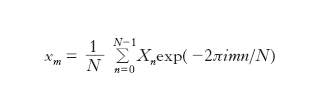DFT
Enciclopedia on line
Sigla di discrete fourier transform, trasformata di Fourier discreta, ossia la restrizione all’insieme di numeri complessi xm, m=0, …, N−1, della trasformata di Fourier di una funzione f(x) (➔ trasformazione). La DFT Xn, n=0, …, N−1, di xm è definita dall’espressione:
Il coefficiente Xn è spesso chiamato n-esimo coefficiente di Fourier di xm. Come per la trasformata di Fourier, si può definire la trasformazione inversa
La DFT è molto studiata in quanto l’applicazione della trasformata di Fourier a problemi trattati con l’ausilio di un elaboratore elettronico coinvolge di fatto la DFT, essendo qualunque funzione approssimata dall’elaboratore tramite una successione finita di valori. In particolare, per calcolare la DFT si utilizzano con il calcolatore algoritmi molto efficienti (FFT), che si basano sulla fattorizzazione del numero N di valori su cui è calcolata la trasformata di Fourier, e sono particolarmente convenienti quando N è una potenza di un numero primo p piccolo. L’idea alla base è quella di utilizzare le proprietà dell’esponenziale complesso, che compare nella trasformata di Fourier discreta, per calcolare quest’ultima attraverso p trasformate di Fourier discrete definite su N/p termini. Ciascuna di queste trasformate può essere calcolata applicando ricorsivamente lo stesso algoritmo. L’economia di calcolo è notevole in quanto, in generale, per calcolare una trasformata di Fourier discreta occorre un numero di operazioni dell’ordine di N2, mentre, utilizzando questi algoritmi, tale numero è dell’ordine di N lnN.
© Istituto della Enciclopedia Italiana - Riproduzione riservata