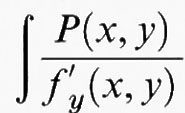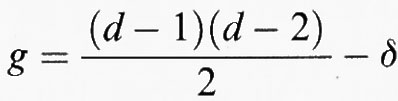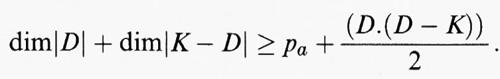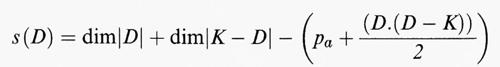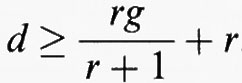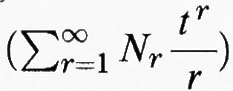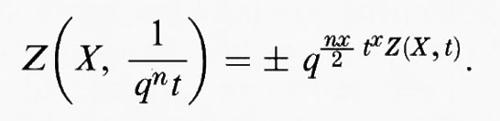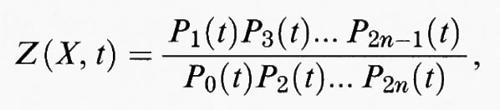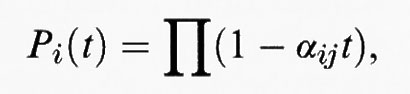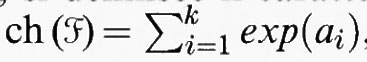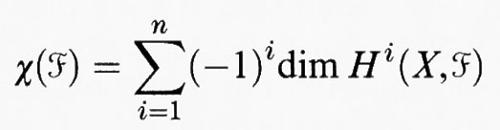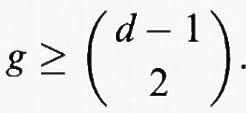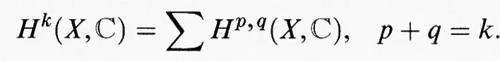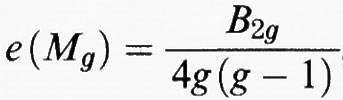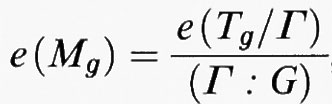Geometria algebrica
Enciclopedia del Novecento II Supplemento (1998)
GEOMETRIA ALGEBRICA
Lo sviluppo delle idee di Ciro Ciliberto
Sommario: 1. I temi classici della geometria algebrica. a) Integrali abeliani e curve algebriche. b) L'approccio geometrico alla teoria delle curve. c) Gli inizi della teoria delle superfici. d) La scuola italiana e la classificazione delle superfici. e) Primi sviluppi dell'indirizzo topologico-analitico dopo Riemann. f) II problema delle varietà di dimensione superiore. 2. Verso nuovi metodi e un nuovo linguaggio algebrico-geometrico. a) Critica dei principî, sviluppo delle tecniche topologico-analitiche e geometria aritmetica. b) I metodi algebrici e coomologici. c) Dai problemi fondazionali alla classificazione delle varietà. □ Bibliografia.
1. I temi classici della geometria algebrica
La geometria algebrica si occupa dello studio delle ‛varietà algebriche', ossia dei sottoinsiemi dello spazio a un numero qualunque di dimensioni definiti da equazioni polinomiali. La presenza dei polinomi è ubiquitaria nella matematica e nelle sue applicazioni: la si rintraccia già nelle ricerche dei matematici greci e la si ritrova via via nei successivi sviluppi della disciplina fino ai nostri giorni. Perciò si può ben dire che la geometria algebrica è una delle branche più classiche della matematica.
Tuttavia, volendo individuare un inizio per i moderni sviluppi di questa disciplina, si può fissare l'attenzione sulla prima metà dell'Ottocento e considerare in particolare esponenti della scuola francese - come G. Monge, C. J. Brianchon, M. Chasles e J. V. Poncelet - e di quella tedesca - come A. F. Moebius, J. Plücker, K. G. C. von Staudt, J. Steiner e infine H. Grassmann. Le ricerche di questi matematici gettano le basi della moderna geometria algebrica con un uso sistematico della geometria proiettiva del piano e dello spazio ordinario nello studio di proprietà di oggetti geometrici ed enti algebrici notevoli (lo spazio ambiente nelle ricerche moderne, infatti, è per lo più lo spazio proiettivo n-dimensionale; v. geometria algebrica: Concetti fondamentali, vol. X - d'ora in avanti, v. Shafarevich - cap. 2, § a). In questo ambito, ad esempio, viene ricostruita e ampliata la teoria delle coniche e delle quadriche dello spazio tridimensionale, rileggendola alla luce di nuove idee come la polarità, e viene intrapreso lo studio locale e globale di curve e superfici algebriche di grado superiore, anche in relazione a questioni di natura numerativa e di teoria degli invarianti. In particolare quest'ultima disciplina, che trova il suo fondamento nelle ricerche aritmetiche di J. L. Lagrange e K. F. Gauss, trae origine appunto dallo sviluppo della geometria proiettiva e dall'esigenza di tradurre in forma analitica proprietà proiettive di figure geometriche ed enti algebrici, e vede i suoi inizi nelle pionieristiche ricerche del matematico inglese G. Boole che studia varie proprietà dei discriminanti di polinomi omogenei in due variabili.
I sostanziali progressi algebrico-geometrici nella prima metà del XIX secolo sono testimoniati da un'ampia trattatistica che comprende testi di vari degli autori citati in precedenza e di altri, quali l'inglese G. Salmon, cui si devono opere fondamentali di geometria proiettiva e di teoria degli invarianti. È notevole peraltro in questi testi la tendenza a includere nella trattazione algebrico-geometrica anche lo studio delle proprietà differenziali di curve e superfici dello spazio ordinario (v. geometria differenziale, vol. III), distinguendo - per la prima volta dopo l'opera fondamentale di Gauss - gli aspetti proiettivi (quali le nozioni di sviluppabilità, di linee asintotiche, ecc.) da quelli metrici (quali la nozione di curvatura, di torsione, ecc.). In tal modo la geometria algebrica, nel suo aspetto proiettivo, si propone come linguaggio universale per la trattazione dei problemi classici dell'algebra e della geometria.
Gli sviluppi successivi prendono le mosse, all'inizio della seconda metà dell'Ottocento, dalle rivoluzionarie ricerche di B. Riemann da un lato e dall'emergere della figura di L. Cremona, il fondatore della scuola italiana di geometria algebrica, dall'altro. A Cremona si deve il merito di aver affinato i metodi della geometria proiettiva con l'uso di tecniche algebriche raffinate, dando un contributo decisivo alla realizzazione del linguaggio algebrico geometrico universale cui si è dianzi accennato e fondando in tal modo un metodo per la trattazione geometrica dei più svariati problemi algebrici. Come esempio, tra i tanti, della validità del metodo di Cremona e del tipo di questioni da lui considerate, basta ricordare la sua brillante dimostrazione geometrica di un teorema algebrico di J. J. Sylvester (1851) che afferma che un polinomio omogeneo di terzo grado in quattro variabili si può scrivere in uno e un sol modo come somma di cinque cubi di polinomi omogenei lineari nelle stesse variabili (v. Cremona, 1868). In questo caso l'approccio di Cremona è basato su un'interpretazione sintetica di concetti riguardanti la teoria degli invarianti che, dopo gli inizi dettati da Boole, si andava in quegli anni sviluppando a opera di J. J. Sylvester e di A. Cayley in Inghilterra e di S. H. Aronhold, A. Clebsch e P. Gordan in Germania.
Il fondamentale merito scientifico di Cremona è stato quello di aver introdotto e studiato, a partire dal 1863, le trasformazioni birazionali dello spazio, trasformazioni che successivamente vennero in suo onore denominate ‛cremoniane' (v. Shafarevich, cap. 2, § a). Questo è un concetto che generalizza quello classico di trasformazione lineare o ‛proiettività': si tratta infatti di traformazioni che sono esprimibili, in termini di coordinate cartesiane, mediante funzioni razionali e che sono generalmente invertibili con funzioni dello stesso tipo. I primi esempi di queste trasformazioni nel piano risalgono a Poncelet (1822), a Plücker (1830) e a Steiner (1832): si tratta delle ‛trasformazioni quadratiche' che mutano rette in coniche. Successivamente, nel 1859, anche il francese E. de Jonquières prese in considerazione trasformazioni del piano di ordine n comunque elevato, che da lui presero il nome: esse trasformano rette in curve piane di ordine n con un dato punto di molteplicità n -1. Tuttavia, Cremona per primo formalizzò la nozione di trasformazione birazionale facendone un uso sistematico per lo studio di enti geometrici notevoli, ad esempio per lo studio delle superfici razionali dello spazio, in particolare per quelle di grado basso.
È significativo nell'apporto di Cremona, cui fa seguito quello della scuola italiana della quale egli fu l'iniziatore, l'individuazione della natura birazionale della classificazione delle varietà algebriche, un'idea nuova rispetto alla letteratura precedente, che costituisce una vera e propria rivoluzione nella geometria algebrica: le varietà vengono, in sostanza, classificate a meno di trasformazioni birazionali, piuttosto che a meno di trasformazioni proiettive. Con ciò non viene a diminuire l'importanza della geometria proiettiva, anzi, come vedremo, essa verrà usata per meglio chiarire le proprietà birazionali delle varietà.
a) Integrali abeliani e curve algebriche
Il concetto stesso di trasformazione birazionale e l'importanza di questa nozione fu probabilmente suggerita a Cremona dalle fondamentali ricerche di Riemann (v., 1857), nelle quali la risoluzione dei classici problemi inerenti agli integrali di funzioni algebriche di una variabile, i cosiddetti ‛integrali abeliani', viene ricondotta allo studio delle curve algebriche su cui gli integrali in questione sono definiti. E lo studio di tali curve, considerate astrattamente come varietà analitiche complesse compatte di dimensione uno (oggi dette superfici di Riemann), è appunto fatto a meno di trasformazioni birazionali delle curve in questione. Che le ricerche di Riemann fossero ben note a Cremona, nonostante il differente tipo di approccio (analitico nel primo, geometrico-proiettivo nel secondo) alle questioni studiate è testimoniato dal fatto che egli ne fece di certo oggetto di vari suoi corsi universitari.
I risultati di Riemann, conseguiti con metodi di analisi e concretizzatisi negli anni 1850-1859, fanno seguito alle ricerche di F. H. Jacobi e di N. H. Abel e coronano un lungo periodo di studi e ricerche sugli integrali abeliani che comprende già i lavori di G. F. Fagnano e di L. Eulero sugli integrali ellittici. Nella teoria di Riemann ha un ruolo fondamentale l'invariante, da lui chiamato Klassenzahl, oggi detto genere (Geschlecht), secondo la più tarda terminologia di Clebsch. Il genere è un invariante topologico: esso è precisamente il ‛numero dei manici' posseduti dalla curva, vista come superficie orientabile e compatta, vale a dire il doppio del genere eguaglia il primo numero di Betti della superficie. Riemann dimostra che questo invariante topologico coincide con l'invariante analitico, introdotto da Abel, dato dal massimo numero di integrali abeliani ovunque regolari (o ‛differenziali olomorfi', secondo la terminologia moderna), linearmente indipendenti sulla curva. Riemann prova inoltre che il genere g entra nella determinazione del massimo numero r di funzioni razionali linearmente indipendenti con dati poli, in numero di n, sulla curva. Si trova infatti che r ≥ n - g + 1, un teorema completato nel 1864 da G. Roch, allievo di Riemann, con l'interpretazione della differenza i = r - n + g - 1 (detta ‛indice di specialità' dell'insieme dei poli) come il massimo numero di differenziali olomorfi linearmente indipendenti nulli nei dati poli (teorema di Riemann-Roch; v. geometria, vol. III). Riemann introduce poi il concetto di trasformazione birazionale tra curve, evidenziando che l'invariante principale per trasformazioni birazionali è il campo delle funzioni razionali su una curva. Egli suddivide infine i campi di funzioni razionali su curve, ossia le curve di genere g a meno di trasformazioni birazionali, in classi che descrivono una varietà Mg, dipendenti da un certo numero di parametri o moduli, che egli valuta in 0 se g = 0, 1 se g = 1 e 3g - 3 se g ≥ 2. La varietà Mg è detta lo ‛spazio dei moduli' delle curve di genere g (v. Shafarevich, cap. 4, § a).
b) L'approccio geometrico alla teoria delle curve
Dopo Riemann, fu particolarmente Clebsch in Germania a sviluppare applicazioni e interpretazioni geometriche della sua teoria (v. Clebsch e Gordan, 1866), legando la nozione di differenziale olomorfo su una curva piana di grado d dotata di soli nodi a quello di curva aggiunta alla curva data, cioè una curva di grado d - 3 passante per tutti i nodi della curva data. In altri termini, se f(x, y) = 0 è l'equazione affine della curva, l'integrale
dx è olomorfo sulla curva se e solo se P(x, y) = 0 è l'equazione di un'aggiunta della curva data, e pertanto il calcolo del genere si riduce a quello della dimensione del sistema delle curve aggiunte di grado d - 3. In tal modo Clebsch trova la formula g =
dove δ è il numero dei nodi. Egli studia poi le curve di genere 0 e 1, provando che le prime sono razionali, ossia birazionali a P1, e che per le seconde, dette curve ellittiche, se realizzate, come sempre è possibile, come curve piane lisce di grado 3, il modulo di Riemann si interpreta in termini di un invariante proiettivo già introdotto da G. Salmon, e cioè il birapporto delle quattro tangenti condotte alla curva di un qualunque suo punto dato.
L'esito di queste applicazioni geometriche è lo sviluppo di un approccio algebrico-geometrico alla teoria analitica riemanniana. Questo complesso e ambizioso programma viene intrapreso negli anni settanta del secolo scorso principalmente da M. Noether, alle cui teorie può esser fatto risalire l'inizio dell'uso di tecniche di algebra commutativa in geometria. Noether pone infatti a fondamento della sua trattazione algebrica della teoria delle curve piane il cosiddetto teorema dell'Af + Bϕ, che fornisce condizioni necessarie e sufficienti affinché un polinomio in due variabili si possa esprimere come combinazione lineare, di due polinomi f e ϕ con coefficienti due altri polinomi A e B. Noether dimostra pure come attraverso trasformazioni cremoniane del piano si possa ridurre ogni curva ad avere singolarità più semplici, dette ‛ordinarie', ossia punti multipli con tangenti distinte, e come ogni curva possegga modelli birazionali lisci in ogni spazio proiettivo di dimensione r ≥ 3 e modelli piani con soli nodi. In una fondamentale memoria (v. Brill e Noether, 1873), facendo tesoro della lezione proiettiva di Cremona, la teoria analitica di Riemann viene tradotta nel rivoluzionario linguaggio geometrico-proiettivo delle serie lineari.
Una serie lineare è una serie di gruppi di punti, oggi detti ‛divisori effettivi' (v. Shafarevich, cap. 2, § b), tagliati sulla curva, pensata immersa in uno spazio proiettivo, dalle ipersuperfici di un sistema lineare dello spazio ambiente, fuori di eventuali punti base del sistema sulla curva. Una pietra miliare della teoria è l'individuazione dello stretto legame tra questo concetto, le applicazioni razionali definite sulla curva a valori in uno spazio proiettivo e l'esistenza di funzioni razionali con dati poli sulla curva. Ad esempio, due divisori E1 ed E2 appartengono a una stessa serie lineare se e solo se esiste una funzione razionale non nulla f tale che il corrispondente divisore (f) (v. Shafaverich, cap. 2, § a) sia uguale a E1 - E2, il che si esprime dicendo che E1 ed E2 sono linearmente equivalenti. In questo ordine di idee, una serie lineare si può riguardare nel seguente modo. Si considera uno spazio vettoriale V di funzioni razionali sulla curva aventi un dato divisore dei poli D: la serie lineare è data dai divisori degli zeri delle funzioni non nulle di V. Se f0, ..., fr è una base di V, allora l'applicazione razionale x → (f0 (x):...:fr (x)) manda la curva in Pr e la serie lineare si può riguardare come tagliata sull'immagine della curva dagli iperpiani di Pr. Una serie lineare si dice ‛completa' se non è contenuta in una serie lineare più ampia. In tal caso essa contiene tutti i divisori effettivi linearmente equivalenti a un suo divisore D, si denota con ∣D∣ e la relativa applicazione razionale si denota col simbolo ϕD.
Tra le serie lineari su una curva riveste particolare importanza la serie canonica ∣K∣ che, dal punto di vista analitico, è la serie dei divisori degli zeri dei differenziali olomorfi sulla curva, mentre, dal punto di vista geometrico, è tagliata, su un modello piano di grado d della curva con soli nodi, dalle curve aggiunte di grado d - 3 fuori dai nodi. L'applicazione ϕK, detta ‛applicazione canonica', è un isomorfismo della curva sulla sua immagine, detta curva canonica, salvo il caso di eccezione in cui la curva sia iperellittica, cioè un rivestimento doppio della retta. Per il teorema di Riemann-Roch una curva canonica di genere g ≥ 3 ha grado 2g - 2 in uno spazio proiettivo di dimensione g - 1. Riferendosi ai modelli piani delle curve con soli nodi e usando le curve aggiunte, Brill e Noether danno una semplice dimostrazione algebrico-geometrica del teorema di Riemann-Roch.
c) Gli inizi della teoria delle superfici
A questo stesso periodo risalgono i primi contributi di Clebsch e Noether alla fondazione della teoria delle superfici, che aveva visto negli anni immediatamente precedenti i suoi primi sviluppi con gli studi di Cremona e dello stesso Clebsch sulle superfici razionali dei primi ordini. La teoria analitica di Riemann non si prestava a una facile estensione al caso delle varietà di dimensione superiore per mancanza di tecniche adeguate e delle necessarie conoscenze sulla topologia delle varietà di dimensione superiore. Per contro, l'approccio algebrico-geometrico alla teoria delle curve suggeriva alcune naturali generalizzazioni.
Il primo a estendere il concetto di genere alle superfici è stato Clebsch, che nel 1868 definisce il ‛genere' p di una superficie come il massimo numero di 2-forme olomorfe linearmente indipendenti sulla superficie, cioè di forme differenziali che, in coordinate locali (z1, z2) sulla superficie, si scrivono come f (z1, z2) dz1 ⋀ dz2, con f (z1, z2) funzione olomorfa di (z1, z2). Noether (1869) legava poi questo concetto a quello di ‛superfici aggiunte' a opportuni modelli della superficie nello spazio tridimensionale, cioè superfici di grado d dotate di singolarità ordinarie, ossia di una curva di punti doppi con al più un numero finito di punti tripli: le superfici aggiunte sono in questo caso superfici di grado d - 4 contenenti la curva dei punti doppi. Un problema naturale consisteva nel trovare un'espressione del genere di una superficie, analoga a quella della formula di Clebsch per il genere di una curva piana con nodi, in termini dei caratteri proiettivi della curva dei punti doppi. Fu un fenomeno sorprendente incontrato studiando tale problema a mettere per la prima volta in risalto una profonda differenza tra il caso delle curve e quello delle superfici.
Proprio in quegli anni (1871) Cayley, aveva dato delle formule per il calcolo della cosiddetta ‛postulazione' di una curva dello spazio. La postulazione di una varietà proiettiva X ⊆ Pr si chiama oggi ‛polinomio di Hilbert' della varietà. Si tratta di un polinomio PX(n) che calcola, per n molto grande, la dimensione dello spazio vettoriale di tutti i polinomi omogenei di grado n in r + 1 variabili che si annullano nei punti della varietà. Il polinomio PX(n) ha grado uguale alla dimensione di X e i suoi coefficienti dipendono dagli invarianti di X. Ad esempio, se X è una curva liscia di grado d e genere g, si ha, come conseguenza del teorema di Riemann-Roch, che PX (n) = nd - g + 1. Fu sorprendente per Cayley e Noether notare che, nel caso delle superfici rigate (ossia contenenti infinite rette) di grado d dello spazio ordinario P3, calcolando il polinomio di Hilbert della curva dei punti doppi per n = d - 4 ne risultava un valore non positivo, e cioè - g, dove g è il genere della curva sezione piana generale della rigata. D'altra parte la presenza di infinite rette sulla superficie comporta che il genere delle rigate sia 0. Noether fu dunque indotto a introdurre accanto al genere p, detto ‛genere geometrico' e denotato con pg, anche il ‛genere aritmetico' o ‛numerico' pa di una superficie, risultante dal suddetto calcolo, per n = d -, del polinomio di Hilbert della curva dei punti doppi di un modello di grado d, con singolarità ordinarie, della superficie in P3. Noether verificò che anche pa è un invariante birazionale, sempre non maggiore di pg, sicché la quantità q = pg - pa, detta ‛irregolarità', è sempre non negativa.
In successive ricerche Noether si dedicò a estendere al caso delle superfici la nozione di serie lineare, pervenendo al concetto di sistema lineare di curve, o divisori effettivi, su una superficie (v. Shafarevich, cap. 2, § b), riuscendo a estendere anche il concetto di serie canonica ∣K∣, detto ‛sistema canonico' nel caso della superficie, e fallendo, invece, nel tentativo di estensione del teorema di Riemman-Roch e del teorema di desingolarizzazione per le superfici. Particolare importanza hanno anche gli studi di Noether su questioni di razionalità delle superfici. A differenza dei suoi predecessori Cremona e Clebsch, Noether non si addentrò in minute classificazioni, ma ricercò criteri generali di razionalità, pervenendo al famoso teorema del 1870 che asserisce che una superficie è razionale se e solo se contiene un sistema lineare di dimensione positiva di curve razionali (v. Noether, 1871). È infine notevole la stima inferiore fornita da Noether per il numero dei moduli M ≥ 10 (pa + 1) - 2 (K.K) da cui dipende una classe di superfici con dati invarianti pa e (K.K) (per la notazione (K.K), che denota l'indice di interferenza di K con se stesso, v. Shafarevich, cap. 2, § a).
d) La scuola italiana e la classificazione delle superfici
A partire dalla fine degli anni ottanta del secolo XIX, l'eredità scientifica di Noether viene raccolta dalla scuola italiana che, sulla scia di Cremona, perfeziona i metodi proiettivi mettendoli alla prova sull'approccio geometrico di Brill e Noether alla teoria delle curve. In questo ordine di idee il personaggio principale è C. Segre che, insieme a E. Bertini e al giovane G. Castelnuovo, inaugura il cosiddetto ‛metodo iperspaziale' per la costruzione della geometria su una curva e in particolare per la dimostrazione del teorema di Riemann-Roch: un metodo basato sull'uso di semplici formule numerative che descrivono le mutue relazioni tra due serie lineari su una curva.
L'anno 1891 segna una decisa evoluzione nella carriera scientifica di Castelnuovo. Vincitore di una cattedra di geometria, da Torino - dove aveva subito la forte influenza di C. Segre - egli si trasferisce a Roma e qui, pur senza abbandonarla, supera la teoria delle curve e si volge decisamente allo studio delle superfici, riprendendo le pionieristiche ricerche di Clebsch e Noether che non avevano visto continuatori per più di un ventennio. Proprio all'inizio del suo periodo romano, Castelnuovo incontra il giovane F. Enriques, che dopo la laurea alla Scuola Normale di Pisa era venuto a Roma per seguire i corsi di Cremona. Castelnuovo - che aveva introdotto a Roma le nuove idee iperspaziali e la geometria birazionale maturate alla scuola di Segre - con grande intuito indirizza il brillante allievo allo studio delle superfici, e nel giro di pochi mesi dalle loro conversazioni emerge un nuovo approccio alla teoria delle superfici, che pur traendo profitto dalle idee di Clebsch e Noether, le ingloba in un quadro più completo i cui tratti salienti sono i seguenti.
Innanzi tutto viene precisata l'idea che lo studio di una superficie algebrica consiste in quello delle famiglie di curve che appartengono alla superficie. Tra queste si evidenziano i sistemi lineari di curve che, come abbiamo già detto, dal punto di vista proiettivo possono essere considerate come le famiglie di curve tagliate sulla superficie da sistemi lineari di ipersuperfici dello spazio proiettivo ambiente, fuori di eventuali curve fisse. Tra i sistemi lineari hanno particolare importanza quelli completi, i quali non sono contenuti in sistemi lineari più ampi. Alle superfici qualunque viene esteso un teorema, provato da Bertini (1880) per le curve piane, secondo il quale la curva generale di un sistema lineare è liscia fuori dei punti base del sistema, cioè dei punti che appartengono a tutte le curve del sistema. Vengono studiati i sistemi continui di curve che non sono lineari, come, ad esempio, il sistema delle rette di una superficie rigata a curve sezioni di genere positivo. Si dimostra che tali sistemi esistono solo sulle superfici irregolari. Si estende il concetto di curva a quello di ‛curva virtuale' o ‛divisore', cioè una combinazione lineare, a coefficienti interi, di un numero finito di curve effettive sulla superficie, si considerano le intersezioni tra divisori su una superficie e si definisce il numero di intersezione (C.D) di due divisori C e D che, nel caso C coincida con D, prende il nome di ‛autointersezione' (C.C) della curva C. Si prende anche in esame la serie lineare tagliata da un dato sistema lineare su una assegnata curva della superficie e, in particolare, si studia la nozione, che risale a Segre, di ‛serie caratteristica' di un sistema lineare: si tratta della serie lineare tagliata su una curva del sistema lineare dalle altre curve del sistema stesso. Quanto al sistema canonico completo ∣K∣ introdotto da Noether, esso viene essenzialmente caratterizzato intrinsecamente con la proprietà che, per ogni curva C della superficie, ∣K + C∣ taglia su C divisori canonici di C: questa è la cosiddetta ‛formula di aggiunzione'. La nozione di genere geometrico viene interpretata come il massimo numero di curve canoniche K linearmente indipendenti sulla superficie e vengono introdotti nuovi invarianti birazionali, i ‛plurigeneri' Pi, vale a dire il massimo numero di curve i-canoniche (cioè che stanno in uno stesso sistema lineare con divisori del tipo iK, ossia linearmente equivalenti a iK) linearmente indipendenti. Di questi nuovi invarianti si apprezza subito, come vedremo, l'importanza nella classificazione, la quale viene ridotta a quella di modelli particolarmente semplici, i modelli minimali, che sono il piano, le superfici rigate e le superfici su cui le curve canoniche hanno intersezione non negativa con ogni curva effettiva della superficie; ciò si esprime, secondo la terminologia moderna, dicendo che le curve canoniche sono ‛numericamente effettive'. Viene infatti studiata la struttura delle applicazioni birazionali tra superfici, mostrando che una curva irriducibile viene contratta da un'applicazione birazionale tra superfici a un punto semplice se e solo se è razionale, di autointersezione almeno - 1, o, come si dice, è una ‛curva eccezionale'. Una curva eccezionale si dice ‛di prima specie' se ha autointersezione - 1, il che equivale a dire che viene contratta da un morfismo birazionale tra superfici a un punto semplice. Una superficie minimale è una superficie priva di curve eccezionali di prima specie. Essa può avere curve eccezionali ‛di seconda specie', cioè con autointersezione almeno 0, ma ciò accade se e solo se la superficie in questione è il piano o una superficie rigata. Viene infine provato il teorema di Riemann-Roch per le superfici nella forma seguente: dato un qualunque divisore D della superficie, per la dimensione del sistema completo ∣D∣ si ha la formula
prende il nome di ‛sovrabbondanza' del sistema e i sistemi con sovrabbondanza nulla vengono detti ‛regolari'. Tutto ciò è esposto in due fondamentali memorie di Enriques (v., 1893 e 1896). L'importanza di queste ricerche è evidente: esse forniranno il quadro di riferimento generale non solo per gli sviluppi della teoria delle superfici ma anche per lo studio di varietà di dimensione superiore intrapreso in quegli anni da G. Fano, allievo di Segre, e dallo stesso Enriques.
Con gli strumenti così forgiati, Castelnuovo ed Enriques affrontano il problema della classificazione che per la prima volta essi, pur riattaccandosi al classico punto di vista di Riemann per la classificazione delle curve, pongono in tutta la sua generalità e modernità: distinguere le classi di equivalenza birazionale delle superfici minimali mediante gli invarianti discreti Pi, pa, e (K.K) e mediante invarianti continui dati dai moduli che descrivono una classe di superfici con dati invarianti. Il primo banco di prova della nuova teoria è la caratterizzazione, mediante l'uso degli invarianti introdotti, delle superfici razionali, un problema già considerato anni addietro da Noether che aveva congetturato che pg = q = 0 fosse condizione necessaria e sufficiente per la razionalità. Si deve a Enriques di aver prodotto, nel 1896, in una lettera diretta a Castelnuovo, il primo controesempio a tale congettura: una superficie di grado 6 di P3 con punti doppi lungo gli spigoli di un tetraedro, avente pg = q = 0 ma P2 = 1, detta poi ‛superficie di Enriques'. Lo studio di questo controesempio conduce Castelnuovo (v., 1894) alla dimostrazione del suo famoso ‛criterio di razionalità': una superficie è razionale se e solo se q = P2 = 0. Questo teorema risponde anche affermativamente al problema di Lüroth per le superfici, consistente nel chiedersi se una varietà unirazionale (cioè tale che esista un'applicazione razionale suriettiva di uno spazio proiettivo sulla varietà) è anche razionale (cioè birazionale a uno spazio proiettivo). J. Lüroth e Clebsch avevano dimostrato che per le curve la risposta è affermativa.
Il criterio di Caltenuovo costituisce il fondamento principale della classificazione, che viene abbozzata da Castelnuovo ed Enriques negli anni successivi. A essi si uniscono, a partire dal 1900, F. Severi e successivamente molti allievi della scuola italiana. Enriques (v., 1914) suddivise le superfici nelle seguenti quattro classi, secondo quella che oggi viene detta ‛dimensione di Kodaira κ' (v. Shafarevich, cap. 2, § b).
1) κ = - ∞: Pi = 0 per ogni i ≥ 1. Le superfici sono razionali se e solo se q = 0 (per il criterio di Castelnuovo) ovvero birazionali a rigate a curve sezioni di genere q se q > 0 (teorema di Enriques, 1905). Enriques mostra che Pi = 0 per ogni i ≥ 1 se e solo se P12 = 0.
2) κ = 0: esiste un i ≥ 1 tale che Pi ≠ 0 e la successione dei plurigeneri è limitata. Allora i plurigeneri valgono 0 o 1 e si hanno le seguenti classi di superfici (v. sotto, § e): a) q = 0, pg = 1, superfici K3, classificate da Enriques (1908) e Severi (1909); b) q = pg = 0, superfici di Enriques, classificate da Enriques (1906); c) q = 2, superfici abeliane, cioè superfici algebriche del tipo ℂ2/Λ dove Λ è un sottogruppo abeliano di rango 4 di ℂ2 che genera ℂ2 come spazio vettoriale sui reali. Esse sono caratterizzate, per un teorema di Enriques (1905), dall'essere q = 2, e pg = P4 = 1; d) q = pg = 1, superfici biellittiche, classificate da Enriques-Severi (1907) e Bagnera-de Franchis (1909).
3) κ = 1: la successione dei plurigeneri Pi non è limitata, ma è superiormente limitata da una funzione lineare in i. La superficie possiede una fibrazione in curve di genere 1 su una curva: si parla allora di superfici ellittiche, che vennero studiate da Enriques a varie riprese tra il 1898 e il 1914.
4) κ = 2: la successione dei plurigeneri Pi non è limitata da una funzione lineare in i. Allora tale successione cresce, per i ≫ 0, quadraticamente con i e le superfici in questione sono dette superfici di tipo generale.
La classe 4) delle superfici di tipo generale è stata più a lungo esplorata dalla scuola italiana ed è quella che ha in seguito fornito i risultati più significativi. Per questa classe di superfici, l'applicazione i-canonica ΦiK ha per immagine una superficie Xi, detto ‛modello i-canonico' di X, birazionale alla superficie X di partenza per i sufficientemente grande. La geometria proiettiva di Xi nel suo spazio di appartenenza riflette le proprietà birazionali di X. Dunque lo studio di queste superfici consiste, in sostanza, nello studio delle loro applicazioni pluricanoniche e nello studio della geometria proiettiva dei modelli pluricanonici, un programma messo a punto da Enriques e dalla sua scuola solo intorno alla metà degli anni quaranta. Il principale risultato in questa direzione è un teorema di Enriques (1946) e Franchetta (1948) che afferma che: se pg > 0 allora Φ3K è birazionale tranne che per pg = 3, (K . K) = 2 e per pg = 2, (K . K) = 1, mentre ΦiK è birazionale per ogni i ≥ 4 (v. Enriques, 1949; v. Franchetta, 1949). Alla base di questo risultato c'è un importante teorema, detto ‛teorema di regolarità dell'aggiunto' che afferma che: se D è una curva aritmeticamente connessa (cioè tale che per ogni suddivisione D = A + B con A, B curve effettive, si ha (A • B) > 0) sulla superficie tale che (D • D) > 0, allora il sistema ∣K + D∣ è regolare. Una prima versione di questo teorema venne fornita da Picard nel 1905 e si riferisce al caso, meno generale, che D sia una sezione iperpiana della superficie. Come vederemo, questi risultati, davvero cruciali in geometria algebrica, sono stati ritrovati ed estesi da vari autori in anni più recenti.
e) Primi sviluppi dell'indirizzo topologico-analitico dopo Riemann
Tornando all'approccio topologico-analitico impiegato da Riemann nello studio delle varietà, in contrasto con quello algebrico-geometrico di Noether e della scuola italiana, esso viene raccolto in Germania soprattutto da F. Klein (v., 1882), cui si deve, ad esempio, la prima dimostrazione dell'irriducibilità dello spazio dei moduli Mg delle curve di genere g per ogni g. Va inoltre segnalata la presenza in Germania di una grande scuola di algebristi, facente capo a Gauss e affermatasi poi con G. P. Dirichlet, E. E. Kummer, R. Dedekind, L. Kronecker, K. Hensel e H. Weber, per citare solo i suoi principali esponenti. Questa scuola certamente influì in maniera determinante sugli sviluppi dell'approccio algebrico-geometrico noetheriano alla teoria delle curve e delle superfici, lo condizionò e ne fu condizionata a sua volta. Basti pensare a una famosa memoria di Dedekind e Weber del 1882 che costituisce la vera base della moderna geometria aritmetica (v. Dedekind, 1930): in essa si pone infatti in evidenza la profonda analogia tra l'algebra, la teoria dei numeri e la geometria algebrica, elaborando una teoria astratta, in termini di posti, valutazioni, ecc. dei campi di funzioni razionali di grado di trascendenza uno su un dato campo, ossia delle curve algebriche (v. algebra, vol. I; v. numeri, teoria dei, vol. IV).
Il punto di vista di Riemann trova anche in Francia importanti continuatori, quali P. Appel, G. Humbert, É. Picard e H. Poincaré. Gli argomenti principalmente studiati sono le varietà abeliane, la topologia delle varietà e l'integrazione delle forme differenziali algebriche in più variabili.
L'origine del concetto generale di varietà abeliana risale a Jacobi e Riemann, cui si deve l'aver associato a ogni curva algebrica C di genere g una varietà abeliana di dimensione g la cosiddetta ‛jacobiana' J(C) della curva. In generale, una varietà abeliana di dimensione g è un toro complesso X = ℂg/L, dove L è un reticolo massimale, cioè un sottogruppo abeliano di rango 2g che genera ℂg come spazio vettoriale sui reali. Inoltre X deve essere una varietà algebrica, il che impone che L verifichi opportune condizioni, dette ‛relazioni bilineari di Riemann', che si traducono nell'esistenza di una forma hermitiana H definita positiva su ℂg, la cui parte immaginaria T assume valori interi su L (v. Shafarevich, cap. 3, §b). La varietà abeliana si dice ‛principalmente polarizzata' se la forma T è simplettica su L. Ad esempio, J(C) è quoziente dello spazio duale V* dello spazio V dei differenziali olomorfi su C, modulo il reticolo H1(C, ℤ). L'inclusione di H1 (C, ℤ) in V* è data da γ ∈ H1 (C, ℤ) → γ* ∈ V*, essendo γ* : ω ∈ V → ∫γ ω ∈ ℂ. Su H1 (C, ℤ) c'è la forma di intersezione degli 1-cicli su C, che risulta simplettica e si può riguardare come la parte immaginaria di una opportuna forma hermitiana su V*. Per tale motivo la varietà J(C) risulta principalmente polarizzata.
Le funzioni razionali su una varietà abeliana X = ℂg/L risultano funzioni meromorfe di g variabili complesse che sono multiplamente periodiche con periodi in L. Esse si esprimono come quozienti di certe funzioni intere aventi opportuni sviluppi in serie di Fourier, le cosiddette ‛funzioni intermediarie' o ‛funzioni theta', già introdotte da Riemann, il cui studio generale fu intrapreso alla fine del secolo scorso da Appel e Humbert. Quest'ultimo in particolare aveva studiato negli anni 1898-1902 il caso delle superfici abeliane e dei loro quozienti irrazionali per gruppi finiti G di trasformazioni birazionali, le cosiddette ‛superfici iperellittiche', senza però pervenire a una loro completa classificazione. Questo problema fu risolto da Enriques e Severi (v., 1909-1910) e da Bagnera e de Franchis (v., 1908) con la determinazione di venti tipi di gruppi finiti G di trasformazioni birazionali di superfici abeliane che danno luogo a sette tipi di quozienti irregolari con pg = q = 1, le superfici biellittiche, tre tipi di superfici di Enriques e undici tipi di superfici K3.
A Picard si deve la prima versione del citato teorema di regolarità dell'aggiunto nonché la prima caratterizzazione delle superfici abeliane (1889) come le uniche superfici di irregolarità 2 e sistema canonico nullo, un risultato ritrovato per via geometrica da Severi nel 1908. A Picard è stata anche attribuita da Castelnuovo l'introduzione della cosiddetta ‛varietà di Picard' Pic0 (X) di una varietà X: essa parametrizza, in sostanza, i sistemi di divisori algebricamente equivalenti a meno di equivalenza lineare.
Ma probabilmente nell'ambito della scuola francese, la figura più importante, in questo ramo di ricerche, è quella di Poincaré, le cui indagini sulla topologia delle varietà contribuiscono a gettare le basi della moderna topologia algebrica. A Poincaré si deve la prima dimostrazione del cosiddetto ‛teorema fondamentale delle superfici irregolari' (v. Poincaré, 1910), il quale afferma che l'irregolarità q di una superficie è uguale alla dimensione dello spazio delle 1-forme olomorfe sulla superficie (che sono le forme differenziali che, in coordinate locali z1 e z2 sulla superficie, si scrivono come f (z1, z2) dz1 + g (z1, z2) dz2, con f (z1, z2) e g (z1, z2) funzioni olomorfe), alla metà del primo numero di Betti della superficie, alla dimensione della varietà di Picard della superficie. Un risultato basilare, provato da Poincaré per via analitica, che raccoglie ed estende vari risultati precedenti di Humbert, Castelnuovo ed Enriques. In particolare quest'ultimo nel 1904 aveva dimostrato, per via algebrico-geometrica che se q > 0 allora la varietà di Picard della superficie ha dimensione positiva, dal che Castelnuovo e Severi (1905) avevano dedotto il teorema fondamentale. La dimostrazione di Enriques era però sbagliata e, nell'ambito della scuola italiana, non si riuscì mai a rimediare a tale errore, e dunque a fornire una dimostrazione geometrica del teorema fondamentale.
f) Il problema delle varietà di dimensione superiore
Lo studio delle varietà di dimensione superiore ha origine presso la scuola italiana soprattutto nell'ambito proiettivo, in relazione a speciali classi di varietà immerse in uno spazio proiettivo: quadriche, grassmanniane, varietà di Veronese, varietà di Segre, varietà rigate, ecc. Accanto allo studio delle proprietà proiettive delle varietà, viene affrontato anche quello della classificazione birazionale, un problema presentatosi ai geometri italiani come la naturale estensione in dimensione superiore della classificazione di curve e superfici. La prima questione impostasi alla loro attenzione, e quella più studiata nell'ambito della geometria birazionale delle varietà, fu il già citato problema di Lüroth, che consiste nel chiedersi se ogni varietà unirazionale sia anche razionale. Come già ricordato, la risposta a questa domanda è affermativa nel caso delle curve (teorema di Clebsch-Lüroth) e delle superfici (teorema di Castelnuovo), ma si deve a Fano e a Enriques l'aver osservato per primi che il problema ha risposta negativa per le varietà di dimensione tre. Furono infatti questi due autori ad affermare che la varietà a tre dimensioni intersezione completa di una ipersuperficie quadrica e di una cubica in uno spazio proiettivo a cinque dimensioni è unirazionale (v. Enriques, 1912) ma non razionale (v. Fano, 1907-1908): un risultato che ha ricevuto però solo in tempi recenti una dimostrazione rigorosa completa (v. cap. 2, § c). Le conseguenze di questa scoperta apparvero subito evidenti: per le varietà di dimensione superiore a due, non è vero che l'annullarsi dei plurigeneri comporti, come per le superfici, che la varietà sia rigata. In particolare non riesce possibile dare un semplice criterio di razionalità, come quello di Castelnuovo per le superfici, basato sull'annullarsi di alcuni invarianti birazionali.
Sul problema di Lüroth e sulle sue implicazioni nella classificazione birazionale delle varietà si sono a lungo concentrati gli sforzi di alcuni esponenti della scuola italiana, che ne intuirono la rilevanza. In particolare furono studiate speciali classi di varietà con i plurigeneri nulli, allo scopo di determinare l'eventuale razionalità, unirazionalità o ‛unirigatezza' (una varietà si dice unirigata se è ricoperta da una famiglia di curve razionali). In questo ordine di idee va segnalato il classico problema della razionalità della ipersuperficie cubica generale dello spazio proiettivo a quattro dimensioni, di cui si sono occupati Fano e U. Morin. Tali ipersuperfici sono unirazionali e alcune di esse, ad esempio quelle dotate di un punto doppio, sono anche razionali. La questione se esse fossero o meno tutte razionali fu considerata già dai geometri della generazione di Noether. Il problema non fu mai risolto dalla scuola italiana, che tuttavia pose le basi necessarie per la sua soluzione negativa, avvenuta solo negli anni settanta (v. cap. 2 § c).
Ancora in merito al problema di Lüroth va segnalata un'altra ricerca di Enriques (v., 1897), che fornisce una risposta negativa alla questione se una varietà a tre dimensioni con un sistema lineare di dimensione positiva di superfici razionali sia a sua volta razionale, mentre, come già detto, l'analoga questione per le superfici ha risposta affermativa (teorema di Noether). L'argomento di Enriques fu poi ripreso da Fano (v., 1918) - che dimostra la razionalità delle varietà a tre dimensioni a superficie sezioni razionali, tranne al più la ipersuperficie cubica su citata - e più tardi da Morin (v., 1939), che fornisce una classificazione di tali varietà. Molto significativa nell'ambito della geometria delle varietà è l'opera di Fano, che fin dal 1908 si occupò dell'importante problema di classificare le varietà aventi l'opposto del sistema canonico ampio (un sistema lineare su una varietà si dice ‛ampio' se esistono modelli proiettivi lisci della varietà su cui gli iperpiani dello spazio ambiente tagliano divisori del sistema o multipli di essi): è chiaro che queste varietà hanno tutti i plurigeneri nulli. Alla considerazione di tali varietà, oggi dette ‛varietà di Fano', si è naturalmente condotti ancora dal problema di Lüroth, e Fano ne abbozza la classificazione in dimensione tre, classificazione solo recentemente ripresa e completata (v. cap. 2, § c).
Un posto di particolare rilievo nello sviluppo della geometria algebrica è quello occupato da Severi, i cui contributi, se pur giudicati in modo controverso, aprirono nuovi orizzonti in questo campo. Egli utilizzò lo strumento proiettivo, tipico della scuola italiana, per chiarire nuovi aspetti e proprietà intrinseci delle varietà. Un bell'esempio di ciò è un famoso teorema del 1901, in cui si dimostra che le ipersuperfici liscie di uno spazio proiettivo di dimensione r ≥ 4 contengono soltanto sottovarietà di codimensione uno che sono intersezione completa con un'altra ipersuperficie dello spazio ambiente (v. Severi, 1906). Tale teorema, che esprime una riposta proprietà topologica delle varietà algebriche, verrà notevolmente esteso da S. Lefschetz nel 1921 (v. cap. 2, § a). Nel 1915 Severi dimostra che sulle varietà grassmanniane G(h, r) che parametrizzano i sottospazi di dimensione h di un fissato spazio proiettivo di dimensione r, le sole sottovarietà di codimensione 1 sono intersezioni complete con ipersuperfici dello spazio ambiente, quando G(h, r) si pensi immersa nello spazio proiettivo con la ben nota ‛immersione di Plücker'.
Molti altri furono gli argomenti toccati da Severi nelle sue ricerche, pur se talora senza riuscire a ottenere risultati completi. Le polemiche suscitate dai suoi metodi, sovente giudicati poco rigorosi fuori della scuola italiana, e i tentativi più recenti di gettare luce su varie sue interessanti affermazioni non sufficientemente giustificate hanno stimolato successivi sviluppi della disciplina. Pertanto è opportuno segnalare qui rapidamente alcuni dei problemi da lui considerati, dei quali successivamente vedremo i più recenti sviluppi.
1. Problema della struttura birazionale dello spazio dei moduli Mg delle curve di genere g. In particolare quando Mg è razionale o unirazionale? Severi (v., 1915) prova, con un'argomentazione incompleta, che Mg è unirazionale per g ≤ 10 e congettura che Mg sia unirazionale per ogni g.
2. Problema dell'irriducibilità della famiglia V (d, δ) delle curve piane irriducibili di grado d con δ nodi, detta poi ‛varietà di Severi'. Severi (v., 1921) dà risposta affermativa al problema, ma l'argomento geometrico da lui utilizzato si rivelò poi incompleto. Da notare che dall'irriducibilità della varietà di Severi segue quella di Mg per ogni g, risultato che, come abbiamo già detto, fu dimostrato per primo da Klein per via topologica.
3. Problema della classificazione delle curve in uno spazio proiettivo di dimensione qualunque. In particolare Severi riprende un'importante affermazione di Brill e Noether (1874), mai dimostrata da questi due autori, che consisteva nello stabilire che per una curva sufficientemente generale di genere g, immersa in uno spazio proiettivo di dimensione r come curva di grado d, si ha
A sua volta, quest'affermazione si basa sul fatto che l'insieme dei divisori di grado d che variano in una serie lineare di dimensione r su una curva di genere g sufficientemente generale è una varietà le cui componenti hanno dimensione r + ρ, dove ρ = (r + 1) (d - r) - rg. Severi (v., 1921) propone un argomento incompleto, basato sull'idea di degenerare la curva generale di genere g a una curva razionale con nodi, successivamente oggetto di analisi da parte di vari autori.
4. Problema della base. Le sottovarietà di data codimensione di una varietà data generano un gruppo libero, il gruppo dei cicli algebrici della data codimensione. In tale gruppo si possono considerare varie relazioni di equivalenza: quella omologica (due varietà sono equivalenti se e solo se sono omologhe), quella algebrica (due sottovarietà sono equivalenti se e solo se sommando a entrambe una stessa sottovarietà si ottengono varietà che appartengono a una stessa famiglia algebrica di sottovarietà), quella razionale (due sottovarietà sono equivalenti se e solo sommando a entrambe una stessa sottovarietà si ottengono varietà che appartengono a una stessa famiglia algebrica di sottovarietà parametrizzata da una curva razionale), ecc. Il problema della base consiste nello studiare il gruppo quoziente per ciascuna di tali relazioni. La questione ha particolare rilevanza, ad esempio, in geometria numerativa, e viene affrontata da Severi in vari lavori (v., ad esempio, Severi, 1934).
5. Problema di Riemann-Roch. Consiste nel calcolare la dimensione di un sistema lineare di divisori su una varietà data, in termini degli invarianti aritmetici della varietà e dei divisori del sistema. Severi e la scuola italiana, nonostante i molteplici contributi in merito non si sono avvicinati alla soluzione del problema se non in casi particolari.
6. I fondamenti della geometria numerativa. Questa disciplina aveva visto nel secolo scorso significativi sviluppi per opera di vari matematici, tra i quali fanno spicco H. G. Zeuthen e H. Schubert. Tuttavia, la mancanza di una sicura base teorica e metodologica della disciplina era evidente già alla fine del secolo scorso: basti pensare che D. Hilbert fa della questione dei fondamenti della geometria numerativa uno dei problemi da lui enunciati nella famosa conferenza al congresso internazionale dei matematici di Parigi del 1900. Severi dedica a questo problema, nell'arco di quasi tutta la sua carriera, notevole attenzione e molti sforzi, che tuttavia non sono riusciti a concretizzarsi in un quadro rigoroso. Anzi, proprio questo è stato il terreno sul quale si sono sviluppate le maggiori critiche al rigore e ai metodi stessi della scuola italiana.
2. Verso nuovi metodi e un nuovo linguaggio algebrico-geometrico
a) Critica dei principî, sviluppo delle tecniche topologico-analitiche e geometria aritmetica
A partire dagli anni venti, in geometria algebrica assumono sempre maggior consistenza alcune tendenze che, sebbene già manifestatesi in precedenza, erano state alquanto emarginate dal prevalere dell'approccio geometrico-proiettivo della scuola italiana. In questo periodo, invece, si affermano definitivamente i metodi analitici e topologici, grazie alla personalità di Lefschetz, il quale intraprende una poderosa opera di risistemazione e reinterpretazione di vari risultati classici delle scuole tedesca, italiana e francese, inglobandoli in una visione unitaria dello studio della topologia delle varietà proiettive e delle relazioni di questa con la loro geometria estrinseca nello spazio proiettivo in cui sono immerse. In una storica memoria, Lefschetz (v., 1921) affronta questo complesso programma ottenendo una notevole mole di risultati fondamentali. Tra questi vale la pena di citare il cosiddetto ‛teorema della sezione iperpiana' che dice che se X è una varietà algebrica liscia e irriducibile di dimensione n e Y ne è una sezione iperpiana liscia, allora la mappa naturale Hq (X, ℂ) → Hq (Y, ℚ) in coomologia indotta dall'inclusione Y → X è un isomorfismo se q ≤ n - 2; ed è iniettiva se q = n - 1. Da questo risultato si deduce, ad esempio, che le varietà lisce intersezioni complete di dimensione n ≥ 3 in uno spazio proiettivo hanno soltanto sottovarietà di codimensione 1 che sono a loro volta complete intersezioni con un'ipersuperficie dello spazio ambiente, il che estende un già citato teorema di Severi (v. cap. 1, § f). Inoltre, usando la nozione dei cosiddetti ‛fasci di Lefschetz' (sistemi lineari di dimensione uno di sezioni iperpiane di una data varietà con buone proprietà geometriche) Lefschetz è in grado di dedurre dal citato teorema un risultato enunciato da Noether, che afferma che la superficie generale di grado d ≥ 4 di P3 possiede soltanto curve che sono intersezioni complete con una curva dello spazio ambiente (teorema di Noether-Lefschetz). Infine, traendo anche profitto dalla teoria delle superfici iperellittiche di Bagnera e de Franchis e da contemporanei lavori sulle varietà abeliane di G. Scorza, Lefschetz elabora una teoria generale di queste varietà, descrivendone divisori, equivalenza lineare, provando per esse il teorema di Riemann-Roch, ecc.
Alle ricerche di Lefschetz fanno seguito quelle di W. D. Hodge e di E. Kähler (v. Shafarevich, cap. 3, § a) le quali si concretizzano intorno agli anni trenta e si sviluppano poi fino agli anni cinquanta. Data una varietà liscia proiettiva X, si possono considerare gli spazi di coomologia Hk (X) introdotti da G. de Rham, costituiti dallo spazio delle k-forme differenziali chiuse, ossia a differenziale nullo, modulo lo spazio delle k-forme differenziali esatte, cioè che sono differenziali di (k - 1)-forme differenziali su X. Il teorema di de Rham afferma che Hk (X) ≃ Hq (X, ℂ) ≃ Hk (X, ℂ)*, l'isomorfismo essendo dato dall'integrazione delle k-forme differenziali lungo i k-cicli di X. Attraverso questa interpretazione degli spazi di coomologia in termini di forme differenziali e usando la teoria delle forme armoniche su X, Hodge dimostra che per una varietà che possegga una metrica kähleriana, in particolare per una varietà liscia proiettiva (la quale eredita la metrica di Fubini-Study dello spazio proiettivo; v. geometria differenziale, vol. III) si ha una decomposizione naturale
Hk (X, ℂ) = ⊕ Hp,q (X, ℂ), p + q = k,
dove Hp,q (X, ℂ) è lo spazio individuato dalle classi, di forme di tipo (p, q) cioè in cui p differenziali sono olomorfi e q antiolomorfi (v. Hodge, 1941). In questo ambito si pone la famosa ‛congettura di Hodge' (v. Shafarevich, cap. 3 § a).
Le ricerche di Lefschetz hanno anche un notevole influsso sul giovane O. Zariski, formatosi alla scuola di Castelnuovo, ma ben presto emigrato negli Stati Uniti, dove fondò la scuola di geometria algebrica fiorita in quel paese dagli anni cinquanta in poi. Zariski, infatti, negli anni venti si occupava anche lui di problemi topologici delle varietà, in particolare del problema, posto da Enriques, dello studio del gruppo fondamentale del complementare, nel piano proiettivo complesso, di una curva algebrica. È famoso al riguardo l'articolo di Zariski (v., 1929) in cui, poggiando sull'irriducibilità della famiglia delle curve piane irriducibili con soli nodi affermata da Severi (v. cap. 1, § f), dimostra che il gruppo fondamentale del complementare di una curva piana con soli nodi è ciclico.
Lo stesso Zariski, insieme a B. L. van der Waerden e A. Weil, si è reso promotore, a partire dagli anni trenta, di una profonda revisione metodologica della geometria algebrica. Di là dagli aspetti polemici che tale revisione ha comportato, essa si è resa necessaria per varie ragioni. Uno dei motivi principali fu probabilmente la necessità di fondare lo studio delle varietà su più solide basi algebriche, in modo da trasferire i risultati della geometria algebrica su un campo qualunque e renderli dunque anche di natura aritmetica. Non a caso Weil nasce come cultore di teoria dei numeri e van der Waerden come algebrista alla scuola di Noether. D'altra parte, i notevoli risultati conseguiti dai geometri della scuola italiana erano stati ottenuti con geniali vedute cui non sempre seguivano accurate dimostrazioni, tavolta per mancanza di strumenti tecnici adeguati alle felici intuizioni. Occorreva dunque creare tali strumenti, spesso riandando alle vere origini della teoria e ridefinendo addirittura i concetti di base, come quelli di varietà, di loro intersezioni, ecc. Il linguaggio algebrico della scuola di Noether apriva la possibilità di questa rifondazione. Infine, l'affermarsi dei metodi topologici e la consapevolezza della loro crescente importanza, richiedeva un loro definitivo inquadramento nell'ambito algebrico-geometrico e nel linguaggio algebrico noetheriano. Questo complesso progetto si concretizzò in varie opere, tra le quali vanno citati i trattati di van der Waerden (v., 1939), di Weil (v., 1947) e di Zariski (v., 1935).
L'esempio forse più notevole di geometria aritmetica, cioè delle interazioni tra geometria algebrica, teoria dei numeri e topologia, in relazione al periodo e agli autori di cui stiamo parlando, è rappresentato dalle cosiddette ‛congetture di Weil' (v. Weil, Number of..., 1949). Data una varietà liscia X di dimensione n definita sul campo Fq con q elementi, si definisce la ‛funzione zeta' di X data da Z(X, t) : = exp
dove Nr è il numero dei punti di X razionali nel campo Fqr con qr elementi. Le congetture di Weil sono le seguenti.
1) Razionalità: Z(X, t) è una funzione razionale, cioè un quoziente di polinomi a coefficienti razionali.
2) Equazione funzionale: se x è l'autointersezione della diagonale in X × X, allora si ha
dove P0 (t) = 1 - t, P2n (t) = 1 - qnt, e, per ogni i = 1, ..., 2n - 1, Pi ha coefficienti interi e si può scrivere come
4) Numeri di Betti: detto bi (X) il grado di Pi (t), allora x = Σ (-1)i bi (X). Inoltre se X è definita sugli interi, bi (X) sono i numeri di Betti di X pensata come varietà analitica complessa.
Uno dei maggiori contributi di Weil è la dimostrazione che le sue congetture valgono per le curve (v. Weil, Sur les courbes..., 1949). La razionalità e l'equazione funzionale seguono dal teorema di Riemann-Roch. L'ipotesi di Riemann segue dalla disuguaglianza ∣Nr - (1 + qr)∣ ≤ 2gqr, dove g è il genere della curva (v. Shafarevich, cap. 5) che Weil deduce da una classica disuguaglianza di Castelnuovo e Severi relativa a certe serie (non lineari) di divisori su una curva.
b) I metodi algebrici e coomologici
La revisione metodologica operata da van der Waerden, Weil e Zariski prepara il terreno per la vera rivoluzione delle tecniche e del linguaggio algebrico-geometrico, avvenuta negli anni cinquanta con l'introduzione di raffinate tecniche di algebra commutativa e omologica, della teoria degli schemi, della teoria dei fasci e delle tecniche coomologiche.
La teoria dei fasci, fondata da J. Leray, deve la sua prima applicazione sistematica in geometria algebrica al fondamentale articolo di J. P. Serre (v., 1955), nel quale viene proposta la definizione di varietà (v. Shafarevich, cap. 2 § a) e vengono interpretati vari invarianti classici delle varietà - ad esempio i generi geometrico, aritmetico, l'irregolarità, ecc. - in termini di teoria dei fasci e di coomologia.
Il punto di vista di Serre viene ripreso e portato avanti da A. Grothendieck in ambiente algebrico-geometrico e da K. Kodaira in ambiente analitico.
Grothendieck si può ritenere il vero fondatore della geometria algebrica moderna. In una lunga serie di articoli pubblicati negli anni sessanta e settanta, egli introduce la nozione di ‛schema', che estende quella di varietà: così come una varietà è ricoperta da aperti che sono varietà affini che si incollano opportunamente tra loro, uno schema è ricoperto da schemi affini che si incollano tra loro. Uno schema affine X è, in breve, assegnato nello spazio affine An dandone le equazioni ovvero dando l'ideale IX di tutti i polinomi dell'anello S dei polinomi in n variabili (cioè le funzioni regolari su An) che si annullano sullo schema. Le funzioni regolari sullo schema sono dunque gli elementi di A (X): 2pt = S/IX, che è il cosiddetto ‛anello delle coordinate' di X. Risulta anche assegnato il ‛fascio strutturale' ℴX di uno schema X, che non è altro che il fascio delle funzioni regolari sugli aperti di X. Si possono, come per le varietà, definire le nozioni di applicazioni regolari e razionali tra schemi. Successivamente, Grothendieck passa a studiare i fasci coerenti che sono, localmente, quozienti di somme dirette finite del fascio strutturale. In particolare, sono coerenti i fasci localmente liberi di rango k, che sono localmente isomorfi a ℴkX: essi sono i fasci di sezioni di fibrati vettoriali (v. geometria differenziale, vol. III) di rango k su X. Esempi di fasci localmente liberi di rango k sono i fasci ΩkX delle k-forme regolari su X varietà liscia. I fasci localmente liberi di rango 1 sono detti ‛fasci invertibili'. Le loro sezioni globali si annullano su divisori effettivi dello schema, e ogni divisore effettivo sullo schema si ottiene in tal modo. Inoltre divisori linearmente equivalenti corrispondono a sezioni dello stesso fascio. In altri termini, il gruppo Cl(X) (v. Shafarevich, cap. 2 § b) - o Pic(X), in quanto è detto anche gruppo di Picard di X - non è altro che il gruppo delle classi di isomorfismo dei fasci invertibili su X. In particolare i divisori canonici sulla varietà X di dimensione n corrispondono alle sezioni del fascio ΩnK, che è perciò detto ‛fascio canonico' di X e si denota anche con il simbolo ωX.
I fasci coerenti hanno buone proprietà coomologiche: ad esempio, se X è uno schema proiettivo, cioè immergibile in uno spazio proiettivo come sottoschema chiuso, e se ℱ è un fascio coerente su X, gli spazi di coomologia Hk(X, ℱ) sono spazi vettoriali di dimensione finita sul campo base, e quindi sono invarianti dello schema e del fascio. Ad esempio, H0 (X, ℱ) è lo spazio vettoriale delle sezioni globali di ℱ su X. In particolare, gli spazi di coomologia Hk (X, ΩhK) sono invarianti dello schema.
Fondamentale, in questo ordine di idee, risulta la scoperta di un teorema di dualità, detta ‛dualità di Serre' (v. Serre, 1955), che afferma quanto segue: se X è liscia irriducibile di dimensione n e se ℱ è un fascio localmente libero su X, si ha un isomorfismo canonico Hk (X, ℱ) ≃ Hn-k (X, ωX ⊗ ℱ*)*, dove l'asterisco in alto indica il passaggio al duale. Questo teorema si estende agli schemi definendo, sotto opportune ipotesi, il ‛fascio dualizzante' ωX.
La coomologia dei fasci coerenti non è l'unica teoria coomologica che si può considerare sugli schemi. Grothendieck e vari suoi allievi, motivati dallo studio dell'aspetto topologico delle congetture di Weil che richiedono la considerazione dei numeri di Betti in situazioni astratte, ne considerano anche altre. Ad esempio, per lo studio delle congetture di Weil e per l'analisi degli aspetti topologici degli schemi, è fondamentale la considerazione della ‛coomologia etale', che, in breve, nasce dalla considerazione della coomologia dei fasci coerenti non solo sullo schema originario X, ma anche su tutti i suoi rivestimenti non ramificati. Il confronto tra le varie teorie coomologiche che possono realizzarsi sulle varietà ha portato Grothendieck al tentativo di elaborare una ‛super-teoria' coomologica che riunisca in sé tutte le altre (v. Grothendieck, 1969), la cosiddetta ‛teoria dei motivi', essendo questi ultimi ‛oggetti' di una categoria che Grothendieck congettura avere ‛buone proprietà'. A ogni varietà viene associato un oggetto di questa categoria, il motivo della varietà, contenente in sè per così dire, tutte le teorie coomologiche sulla varietà, cioè è il motivo comune di tutte queste teorie. I vari invarianti coomologici si ottengono per realizzazione del motivo in ogni singola teoria coomologica.
Fra i principali risultati di Grothendieck e della sua scuola, devono senz'altro essere annoverati la soluzione generale del problema di Riemann-Roch (teorema di Grothendieck-Riemann-Roch) e la soluzione delle congetture di Weil. Il torema di Grothendieck-Riemann-Roch, nella forma datagli da Grothendieck nel 1971 si riferisce alla seguente situazione. Sia ℱ un fascio localmente libero di rango k su una varietà X. Si può considerare il polinomio di Chern ct (ℱ) di ℱ dato da ct (ℱ)= c0 (ℱ) + c1 (ℱ) t + ... + ck (ℱ) tk, dove ci (ℱ) è la i-esima classe di Chern di ℱ, i = 0, ..., k (v. geometria differenziale, vol. III). Scritto formalmente ct (ℱ) = Π (1 + ait), si definisce il carattere di Chern esponenziale di ℱ come ch (ℱ) =
Sia ora f:X → Y un morfismo tra varietà lisce con fibre liscie e proiettive. Per ogni fascio ℱ localmente libero su X, si definisce un fascio f! (ℱ) su Y che, in breve, è il fascio delle sezioni del fibrato che ha per fibra, in ogni punto y ∈ Y, la coomologia, presa con segni alterni, di ℱ ristretto alla fibra di f su y. La formula di Grothendieck-Riemann-Roch asserisce che
ch (f! (ℱ)) = f*(ch (ℱ)). td(Tf)),
dove Tf è il fascio tangente relativo a f, cioè il fascio dei campi di vettori tangenti a X lungo le fibre di f e dove f* indica l'immagine diretta in coomologia. Nel caso Y sia un punto e X una varietà di dimensione n, si ha la cosiddetta formula di Hirzebruch-Riemann-Roch
χ(ℱ)= deg((ch(ℱ).td(TX))n),
dove TX è il fascio tangente di X, cioè il fascio dei campi di vettori tangenti a X, e (ch(ℱ). td(TX))n è il termine di grado n del relativo sviluppo in serie di potenze in t. Tale termine vive in H2n (X, ℤ) e il suo grado deg ((ch(ℱ). td(TX))n) è un intero. Invece per definizione si ha
ed è facile riconoscere che, nel caso di curve e superfici e per fibrati lineari - corrispondenti, come si è detto, a classi di equivalenza lineare di divisori sulla varietà - si ritrovano, a partire dalla formula di Hirzebruch-Riemann-Roch, i teoremi di Riemann-Roch classici. La formula di Hirzebruch-Riemann-Roch è stata dapprima dimostrata in ambiente analitico complesso da Hirzebruch (v., 1956).
Quanto alle congetture di Weil per varietà di dimensione qualunque, la razionalità della funzione zeta e l'equazione funzionale sono state provate da Dwork (v., 1960) usando metodi di analisi p-adica (v. algebra, vol. I; v. analisi matematica, vol. I). Gran parte delle indagini successive sulle congetture di Weil è stata incentrata sulla ricerca di una buona teoria coomologica per varietà definite su un campo qualunque, allo scopo di dare una giusta definizione dei numeri di Betti della varietà. Ad esempio, l'introduzione della coomologia etale ha consentito a Grothendieck (v., 1964-1965) di dare una nuova dimostrazione della razionalità della funzione zeta e dell'equazione funzionale. L'analogo dell'ipotesi di Riemann è stato dimostrato da Deligne (v., 1974) estendendo a varietà algebriche astratte teoremi noti per varietà complesse e relativi alla teoria di Hodge.
L'introduzione dei metodi coomologici ha anche permesso di gettare luce su alcuni tra i problemi classici più intricati in geometria algebrica, come la determinazione del numero dei moduli da cui dipende una varietà e lo studio delle famiglie di curve su superfici irregolari (cioè il teorema fondamentale delle superfici irregolari). Ad esempio, il problema locale dei moduli, cioè le piccole deformazioni di una varietà, è stato affrontato da Kodaira dal punto di vista analitico (v. Morrow e Kodaira, 1971) e da Grothendieck (v., 1960-1961) da quello algebrico; essi hanno provato che, data una varietà algebrica proiettiva liscia X, lo spazio tangente alla varietà dei moduli nel punto corrispondente a X è dato da H1 (X, ℑX), e che lo spazio dei moduli in questione è liscio nel punto corrispondente a X se H2 (X, ℑX) = 0. Inoltre, una stima inferiore per la dimensione dello spazio dei moduli in un intorno del punto corrispondente a X è data da - χ (ℑX). Similmente, se Y è una sottovarietà chiusa e liscia di una varietà proiettiva liscia X, si può definire il ‛fascio normale' NY∣X di Y in X, che è il fascio dei campi di vettori tangenti a X e normali a Y, cioè il fascio (ℑX)∣Y/ℑY. Lo spazio H0(Y, NY∣X) delle sezioni globali di tale fascio è lo spazio tangente alle deformazioni di Y in X, e tale spazio è liscio se H1 (Y, NY∣X) = 0. Inoltre, una stima inferiore per la dimensione di tale spazio di deformazioni è data da χ(NY∣X). Usando questa teoria si dimostra ad esempio la formula di Noether per il numero dei moduli M di una superficie X (cap. 1, § c), che non è altro che la formula M ≥-χ(ℑX), e si può finalmente provare in ambiente algebrico-geometrico il teorema fondamentale delle superfici irregolari (cap. 1, § e), la cui dimostrazione è dovuta a Mumford (v., 1966).
I metodi di algebra commutativa e omologica (v. algebra, vol. I), che sono alla base della teoria astratta delle varietà e degli schemi, hanno consentito anche la soluzione di un altro problema classicamente insoluto, cioè quello della risoluzione delle singolarità delle varietà algebriche. Il problema generale è il seguente: data una varietà algebrica irriducibile X, trovare una varietà liscia X′ e un morfismo birazionale f:X′ → X. La risoluzione delle singolarità delle curve è nota fin dal secolo scorso: ad esempio, come già ricordato (v. cap. 1, § b), Noether dimostra che ogni curva ha un modello liscio nello spazio a tre dimensioni. Il caso delle superfici è assai più delicato. I geometri della scuola italiana hanno a lungo tentato una dimostrazione del teorema di esistenza della risoluzione delle singolarità, e i tentativi più interessanti si devono a B. Levi, allievo di Segre, a O. Chisini, allievo di Enriques, e a G. Albanese. Tuttavia, la prima dimostrazione completa e rigorosa relativa al caso delle superfici sul campo complesso è dovuta a R. Walker (v., 1935), mentre la prima dimostrazione del caso delle varietà di dimensione tre su un qualunque campo di caratteristica 0 si deve a Zariski (v., 1944). Solo nel 1964 Hironaka, usando tutta la potenza dei metodi algebrici, ha dimostrato la risoluzione delle singolarità per varietà di dimensione qualunque su un campo di caratteristica 0 (v. Hironaka, 1964).
Legato al problema dell'esistenza della risoluzione delle singolarità è quello della struttura delle applicazioni razionali, in particolare di quelle birazionali, tra varietà. Come abbiamo già visto nel caso delle superfici, questo è un problema cruciale per la classificazione. Un importante risultato generale dovuto a Zariski (v., 1955; v. anche Shafarevich, cap. 3, § c) afferma che, se f:X′ → X è un'applicazione birazionale tra varietà proiettive e se X′ è liscia, l'insieme dei punti di indeterminazione di f, cioè i punti dove f non è definita, è una sottovarietà chiusa Z di codimensione almeno 2. Se P appartiene a Z, allora l'applicazione inversa contrae in P una sottovarietà connessa f(P) di dimensione almeno 1. Il teorema vale in ipotesi più deboli della liscezza per X′: basta che X′ sia normale, cioè che si possa ricoprire con aperti affini i cui anelli delle coordinate siano integralmente chiusi (v. algebra, vol. I).
Per le curve proiettive lisce ogni applicazione birazionale è un isomorfismo. Per le superfici lisce ogni applicazione birazionale si può fattorizzare in una successione di ‛dilatazioni' o ‛scoppiamenti' in punti o loro inversi. Un analogo teorema non vale in dimensione maggiore di due; tuttavia, Hironaka (v., 1962) ha dimostrato, come conseguenza del teorema di esistenza della risoluzione delle singolarità, che, data un'applicazione birazionale tra varietà f:X′ → X lisce su un campo di caratteristica zero, esiste un morfismo g:X′′ → X′ che è una successione di scoppiamenti lungo sottovarietà lisce di X′ tale che f 0 g è un morfismo: questo è il cosiddetto teorema di eliminazione delle indeterminazioni, che costituisce un risultato assai importante in quanto da esso segue l'invarianza birazionale di certi caratteri quali, ad esempio, il genere aritmetico, il genere geometrico, ecc., di una varietà.
c) Dai problemi fondazionali alla classificazione delle varietà.
La teoria degli schemi di Grothendieck e la conseguente risoluzione di alcuni dei problemi basilari che, come abbiamo visto, erano rimasti aperti fin dai primi sviluppi della disciplina, ha consentito, a partire dagli inizi degli anni sessanta, una poderosa ripresa della ricerca sui temi classici concernenti la classificazione delle varietà. È stato possibile cioè ritornare su molti degli argomenti pionieristicamente affrontati, talora con strumenti tecnici inadeguati, da Noether e dalla sua scuola e dai geometri algebrici italiani, colmando varie lacune dimostrative o fornendo per la prima volta dimostrazioni complete di teoremi importanti, provando congetture fondamentali rimaste insolute per vari decenni e aprendo la strada per importanti nuovi filoni di ricerca.
Per quanto concerne la teoria delle curve (v. Shafarevich, cap. 4, § a), uno dei più importanti temi di ricerca riguarda lo studio dello spazio dei moduli Mg delle curve di genere g. La prima dimostrazione algebrico-geometrica completa dell'esistenza di Mg come varietà quasi proiettiva di dimensione 3g - per g ≥ 2, è stata data da Mumford nel 1965 (v. Mumford e Fogarty, 1982). Successivamente, Deligne e Mumford (v., 1969) provano per via algebrico-geometrica il teorema dimostrato da Klein per via topologica (v. cap. 1, § 5), secondo il quale Mg è irriducibile. Essi determinano anche una ‛compattificazione naturale' Mg di ¯Mg, che è una varietà proiettiva, i cui punti corrispondono a classi di isomorfismo delle cosiddette curve stabili, cioè curve riducibili, connesse, di genere aritmetico g, dotate di soli nodi aventi un numero finito di automorfismi. Come abbiamo già visto (v. cap. 1, § f), l'irriducibilità di Mg segue anche dall'irriducibilità delle varietà di Severi delle curve piane con nodi, la cui dimostrazione è stata fornita da J. Harris (v., 1986).
Disporre di una compattificazione di Mg è importante se si vuole, ad esempio, studiare le intersezioni delle sottovarietà di Mg anche in relazione a problemi di natura numerativa. Questo punto di vista è stato introdotto da Mumford (v., 1983), il quale iniziò a studiare l'anello di coomologia di Mg o di ¯Mg: in particolare, le sottovarietà algebriche dello spazio dei moduli danno luogo a classi in tale anello e la classe dell'intersezione di sottovarietà è nota se è nota la struttura dell'anello. Mumford determina alcune classi di coomologia, dette ‛classi tautologiche', che, secondo una sua congettura, dovrebbero generare la coomologia dello spazio dei moduli almeno in codimensione bassa. Tali questioni si legano naturalmente allo studio della topologia di Mg e di ¯Mg, che si può anche studiare ricorrendo alla rappresentazione di Mg come quoziente per un gruppo discreto Γ di automorfismi di un dominio limitato Tg ⊂ ℂ3g-3. Questa rappresentazione è dovuta a O. Teichmüller (v., 1944) e conduce a una rappresentazione combinatoria di Mg che risulta particolarmente utile quando si voglia studiare la sua omologia. È usando questa rappresentazione che J. Harer (v., 1983) ha potuto, ad esempio, determinare la struttura degli spazi H2(Mg, ℚ) e H2 (¯Mg, ℚ), (dove ℚ è il campo dei numeri razionali) e, di conseguenza, i gruppi di Picard di Mg e di ¯Mg. È ancora usando queste idee che Harer e D. Zagier (v., 1986) sono riusciti a ottenere l'eccezionale risultato di calcolare la caratteristica di Eulero-Poincaré dello spazio dei moduli. (Per le connessioni tra lo studio di Mg e recenti teorie fisiche, ad esempio, la teoria delle stringhe, v. Shafarevich, cap. 5).
Lo studio dello spazio dei moduli Mg si lega a quello dello spazio dei moduli Ag delle varietà abeliane di dimensione g principalmente polarizzate (v. cap. 1, § e; v. anche Shafarevich, cap. 3, § b). Ag risulta il quoziente del semipiano superiore di Siegel Hg per l'azione del gruppo simplettico intero Γ = Sp(2g, ℤ). Come accennato in precedenza, esiste un'applicazione regolare naturale t:Mg → Ag, detta ‛mappa di Torelli', che associa alla classe di isomorfismo di una curva la classe di isomorfismo della sua jacobiana. Tale mappa è iniettiva, in virtù di un ben noto teorema di R. Torelli (v., 1913). Dunque, essenzialmente Mg si può riguardare come sottovarietà di Ag, ed è chiaro perciò che una buona conoscenza di Ag e delle sue sottovarietà può essere utile per la comprensione di Mg. Questa filosofia riesce utile però solo in parte, in quanto è abbastanza intricata la comprensione dell'immersione t:Mg → Ag. Ad esempio, solo recentemente è stata data risposta, da E. Arbarello e C. De Concini (v., 1984), alla basilare questione nota come problema di Schottky di determinare delle equazioni che definiscano in Hg il luogo delle matrici che corrispondono a jacobiane di curve di genere g.
Per quanto concerne la struttura birazionale di Mg, problema già considerato da Severi, il risultato principale è che Mg è una varietà di tipo generale per g ≥ 24, e ha dimensione di Kodaira positiva se g = 23. La dimostrazione di tale teorema (v. Eisenbud e Harris, 1984; v. Harris e Mumford, 1982) smentisce la congettura di Severi sull'unirazionalità di Mg per ogni g. D'altra parte, l'argomento di Severi sull'unirazionalità di Mg per g ≤ 10 è stato reso rigoroso da Arbarello e Sernesi (v., 1979) ed è stato provato che Mg è unirazionale per g = 12 (v. Sernesi, 1981) e per g = 11,13 (v. Chang e Ran, 1984) e di dimensione di Kodaira negativa per g = 15. La struttura birazionale di Mg è ancora ignota per g = 14,16,...,22.
Sul versante della teoria classica dello studio delle serie lineari su curve, sono stati effettuati progressi non meno significativi. Il risultato principale è la dimostrazione (v. Kempf, 1971; v. Kleiman e Laksov, 1972; v. Griffiths e Harris, 1980) del teorema di Brill-Noether, già considerato da Severi, che afferma che: data una qualunque curva C di genere g, se ρ = (r + 1) (d - r) - r ≥ 0 allora esiste una serie lineare di grado d e dimensione r su C , mentre, se C è sufficientemente generale in Mg, allora se ρ〈0 non vi sono serie lineari di grado d e dimensione r su C, e invece se ρ ≥ 0 la famiglia di tali serie lineari ha dimensione esattamente uguale a ρ. Inoltre tale varietà è non singolare tranne che lungo i punti corrispondenti a serie di dimensione almeno r + 1 (v. Gieseker, 1982).
In relazione alle curve immerse in spazi proiettivi, i risultati più significati si sono avuti per lo studio delle curve canoniche C lisce, di grado 2g - 2 e genere g in Pg-1 (v. cap. 1, § b). Riprendendo un lavoro di K. Petri, un allievo di Noether, B. Saint-Donat (v., 1973) ha dimostrato che a meno che C non sia una curva di grado 5 nel piano, ovvero abbia un morfismo di grado tre su P1, l'ideale IC dei polinomi omogenei in g variabili nulli su C è generato da quadriche. Più recentemente M. Green (v., 1982) ha formulato una congettura assai generale che lega proprietà omologiche dell'ideale IC con proprietà geometriche della curva C. Il teorema di Saint-Donat e Petri è solo il primo caso della congettura di Green.
Per quanto riguarda la teoria delle superfici algebriche, una poderosa spinta agli sviluppi più recenti è venuta dai lavori di Shafarevich (v., 1967) e da una serie di lavori di Kodaira (v., 1975) nei quali viene ripresa la classificazione di Enriques, estesa da Kodaira anche a superfici complesse compatte non algebriche (v. Shafarevich, cap. 4, § d) e vengono studiati alcuni tra i problemi basilari della teoria delle superfici, come il già ricordato problema locale dei moduli. I risultati più importanti sono probabilmente quelli relativi alle superfici di tipo generale. Innanzitutto in un fondamentale articolo di E. Bombieri (v., 1971) viene riconsiderato il problema dello studio delle mappe pluricanoniche per superfici di tipo generale, già affrontato da Enriques e dalla sua scuola. Si ritrovano e si estendono qui i risultati classici, avviando un filone di ricerca non ancora esaurito. Così come nel caso classico, anche in questo caso un ruolo fondamentale viene giocato dal teorema di regolarità dell'aggiunto ritrovato in forma coomologica da C. P. Ramanujam (v., 1972 e 1974): se D è un divisore aritmeticamente connesso su una superficie proiettiva e liscia X, tale che (D.D) > 0, e se ℒ è il fibrato lineare associato a D, allora H1 (X, ℒ*) = 0. L'analogo teorema nel caso che D sia ampio - che, come già ricordato, risale a Picard - è stato esteso a varietà di dimensione qualunque e afferma che, se D è ampio, Hi (X, ℒ*) = 0 se 0 〈 i 〈 dim(X) (v. Kodaira, 1952). Un'ulteriore estensione al caso in cui D non sia necessariamente ampio gioca un ruolo essenziale nei più recenti sviluppi sulla classificazione delle varietà di dimensione superiore (v. Kawamata, 1982; v. Vieweg, 1982).
Un risultato classico di Noether afferma che per ogni superficie minimale si ha (K.K) ≥ 2pa - 4. È invece assai più recente la disuguaglianza di Miyaoka-Yau, che afferma che per ogni superficie si ha K2 ≤ 9 (pa + 1) (v. Miyaoka, 1977; v. Yau, 1977). Un importante risultato di U. Persson (v., 1981) è che quasi tutte le coppie (a, b) con 2b - 4 ≤ a≤9 (a + 1) sono realizzate come invarianti (K.K) = a e pa = b per superfici di tipo generale. Un altro risultato assai illuminante, dovuto a F. Catanese (v., 1984), riguarda invece la struttura dello spazio dei moduli delle superfici di tipo generale con dati invarianti K2 e pa. Catanese, in breve, dimostra che sovente tale spazio dei moduli è riducibile in un numero di componenti irriducibili che cresce al crescere degli invarianti. Questo è un aspetto di sostanziale diversità tra il caso delle curve e quello delle superfici, anche se non è noto se classi di superfici diffeomorfe possano appartenere a componenti distinte dello spazio dei moduli (v. Shafarevich, cap. 4, § b).
Assai suggestive sono le connessioni tra la teoria delle superfici e lo studio delle 4-varietà topologiche o differenziali (v. geometria differenziale, vol. III).
Ad esempio, secondo un fondamentale risultato ottenuto da Freedman (v., 1982), la struttura topologica di una 4-varietà compatta orientabile e semplicemente connessa X è determinata dalla forma di intersezione su H2 (X, ℤ). D'altra parte, se X è una superficie algebrica, la forma d'intersezione è determinata da (K.K), dalla divisibilità della classe di K in H2 (X, ℤ) e dalla caratteristica di Eulero-Poincaré e (X) di X. Da notare che una formula classica di Noether dà e (X) = (K.K) - 12 (pa + 1). In definitiva, la struttura topologica di X è determinata da (K.K), da pa e dalla divisibilità della classe di K in H2 (X, ℤ). La classificazione dal punto di vista differenziabile è invece assai più complicata. Vi sono infatti superfici che sono omeomorfe ma non diffeomorfe. Il primo esempio è stato fornito da Donaldson (v., 1987), che ha anche definito degli importanti invarianti differenziabili, i cosiddetti ‛polinomi di Donaldson', mediante i quali si spera di poter distinguere superfici omeomorfe ma non diffeomorfe. Recentemente interessanti legami della teoria di Donaldson con l'analisi e la fisica sono stati messi in luce da Seiberg e Witten, i quali hanno definito dei nuovi invarianti legati al numero di soluzioni di certe equazioni differenziali non lineari sulle 4-varietà, le cosiddette equazioni di vortice (v. Witten, 1994). Gli invarianti di Seiberg-Witten sembrano essere più maneggevoli dei polinomi di Donaldson, e hanno recentemente permesso a Kronheimer e Mrowka di dimostrare una congettura ormai classica di R. Thom, che afferma che una superficie differenziabile orientabile e compatta S immersa in P2 e omologa a d volte una retta ha genere
Un altro problema, già affrontato da Severi, sul quale le tecniche più moderne hanno gettato nuova luce è quello dello studio dell'equivalenza razionale di 0-cicli su una superficie. La fase moderna della ricerca su questo argomento inizia con i lavori di C. Chevalley (v., 1958) e P. Samuel (v., 1956) i quali definiscono in generale, data una varietà liscia X, l'anello di Chow A(X), che è il quoziente del gruppo dei cicli di X per l'equivalenza razionale. La struttura di anello è data dall'usuale intersezione. Da notare che A(X) è graduato dalla dimensione dei cicli: l'insieme delle classi di equivalenza razionale dei cicli di dimensione i si denota con Ai (X). Per quanto concerne le superfici, hanno importanza i cicli di dimensione 0, in quanto A0 (X) = ℤ e A1 (X) = Pic (X) sono oggetti già noti. Ai cicli 0-dimensionali si può associare il ‛grado', cioè il numero dei punti di cui un ciclo è composto, e il grado è invariante per equivalenza razionale. Quindi si indica con A0d (X) l'insieme delle classi dei cicli 0-dimensionali di X di grado d. È chiaro che al fine di comprendere la struttura di A0 (X) basta capire la struttura di A00 (X), che è un gruppo. Ebbene, Mumford (v., 1969) ha dimostrato che se pg > 0, allora A00 (X) è essenzialmente una varietà di dimensione infinita. Il caso pg = 0 è particolarmente interessante: esso è stato esaminato da S. Bloch (v. Bloch e altri, 1976), che ha congetturato che se pg = 0, allora A00 (X) coincide con la cosiddetta ‛varietà di Albanese' di X. Questa è una varietà abeliana, analoga per X alla jacobiana di una curva: essa si definisce come V*/H1 (X, -ℤ)0, dove V è lo spazio delle 1-forme olomorfe su X, mentre H1 (X, -ℤ)0 è H1 (X, ℤ) modulo la torsione. Questa congettura è stata dimostrata da Bloch e altri (v., 1976) per le superfici non di tipo generale, ma è tuttora aperta per queste ultime. Passi importanti verso la sua dimostrazione sono stati compiuti da Roitman (v., 1972 e 1980), il quale ha dimostrato che la congettura è vera se A00 (X) ha dimensione finita, e che in ogni caso A00 (X) e Alb (X) hanno lo stesso sottogruppo di torsione.
Sullo studio del problema di Lüroth, ossia su questioni di razionalità per varietà di dimensione tre o maggiore, l'impatto delle tecniche moderne è stato particolarmente significativo. Ad esempio, Clemens e Griffiths (v., 1972) hanno finalmente dimostrato che l'ipersuperficie cubica generale X di P4 non è razionale (v. cap. 1, § e). L'idea di Clemens e Griffiths consiste nel considerare una varietà abeliana J(X) legata a X, detta jacobiana intermediaria di X, e nel provare che questa non è una jacobiana o un prodotto di jacobiane di curve, come invece dovrebbe essere se X fosse razionale. Un metodo, questo, che funziona in situazioni più generali del caso in esame. Ancora in relazione al problema di Lüroth, un metodo del tutto diverso per scoprire se una data varietà X è razionale è quello di studiarne il gruppo Bir(X) delle trasformazioni birazionali in sé. Usando questa idea, Iskohvskih (v., 1979) ha fornito la prima dimostrazione che l'esempio di Enriques-Fano, cioè l'intersezione completa liscia di una quadrica e di una cubica in P5, non è razionale.
Quanto alla classificazione generale delle varietà di dimensione tre, rimandiamo a Shafarevich, cap. 2, § b, e cap. 4, § c. I più recenti sviluppi sono dovuti in gran parte alla scuola giapponese e in particolare a S. Mori (v., 1985; v. Mori e Mukai, 1981), il cui programma consente in definitiva di realizzare uno schema generale della classificazione delle varietà di dimensione tre sostanzialmente analogo a quello esistente per la classificazione delle superfici. Alla base della teoria di Mori troviamo il teorema di contrazione dei raggi estremali e la caratterizzazione delle singolarità che nascono da tali contrazioni, riducibili mediante singolarità abbastanza semplici, dette singolarità terminali. Dai risultati di Mori, in particolare, discende la dimostrazione per le varietà di dimensione tre della congettura della generazione finita; la classificazione minuta è tuttavia ancora lontana. Solo per alcuni tipi di varietà si hanno risultati più precisi: tra questi, la classe più importante è forse quella delle varietà di Fano, ormai completamente classificate (v. Iskohvskih, 1977 e 1978; v. Shokurov, Smoothness of..., e The existence..., 1980; v. Mori e Mukai, 1981). I casi considerati da Iskohvskih e Shokurov sono quelli delle varietà di Fano X della serie principale, cioè aventi il secondo numero di Betti B2 uguale a 1. Questi casi erano già stati considerati da Fano e la classificazione di Iskohvskih sostanzialmente conferma quella di Fano. Invece il caso B2 ≥ 2, considerato da Mori e Mukai, è assai più complicato e del tutto nuovo rispetto alla letteratura classica. Il programma di Mori si può applicare, in linea di principio, anche a varietà di dimensione maggiore di tre, ma le difficoltà tecniche che si incontrano su questa strada si sono finora dimostrate difficili da sormontare e pertanto i risultati generali relativi alla classificazione delle varietà di dimensione n ≥ 4 sono per il momento scarsi.
Un argomento che non trova molti riscontri classici, ma che invece ha visto un poderoso sviluppo in tempi recenti, è lo studio e la classificazione proiettiva di sottovarietà proiettive lisce X di data dimensione n in uno spazio proiettivo Pr sui complessi. Mentre ogni varietà X di dimensione n può essere immersa in Pr, con r ≥ 2n + 1, la sorprendente filosofia che emerge dagli studi degli ultimi trent'anni è che, se la codimensione e = r - n è bassa allora vi sono poche varietà lisce X in Pr, in sostanza solo le varietà intersezioni complete di ipersuperfici. Questa filosofia è espressa dalle ‛congetture di Hartshorne' che affermano che: 1) se X è liscia e 2e 〈 n, allora X è intersezione completa; 2) se X è liscia e 2e - 2 〈 n, allora X è linearmente normale, cioè non esiste alcuna varietà Y ⊂ Pr+1 tale che X sia proiezione di Y da un punto esterno a Y su un iperpiano (v. Hartshorne, 1974). Probabilmente, il principale motivo che ha indotto Hartshorne a formulare queste congetture risiede in un teorema di Barth e Larsen (v., 1972), che, estendendo il teorema della sezione iperpiana di Lefschetz (v. cap. 2, § a), afferma che le varietà di codimensione bassa hanno coomologia uguale a quella delle intersezioni complete della stessa codimensione. La prima di queste congetture resta tuttora un problema aperto, perfino nel caso più semplice e = 2, nel quale la congettura si applica a varietà di codimensione 2 in Pr, con r ≥ 7, ed equivale alla seguente: ogni fibrato vettoriale di rango 2 su Pr, con r ≥ 7, è somma diretta di fibrati lineari. Peraltro, si ritiene che la congettura valga anche nel caso r = 6. Di certo non vale per r ≤ 5. Tuttavia si hanno risultati sorprendenti anche per le sottovarietà lisce di codimensione due in Pr, per r = 4, 5. Si pensi che, per un teorema di Ellingsrud e Peskine (v., 1989), il grado d delle superfici lisce di P4 che non sono di tipo generale è limitato. Finora si sa che d ≤ 105, ma non si conoscono esempi per d ≥ 16 ed è probabile che non ne esistano affatto.
La seconda congettura di Hartshorne è invece stata dimostrata da F. Zak, che ha anche dato la classificazione delle varietà lisce, non linearmente normali, con 2e - 2 = n, da lui dette varietà di Severi. Il primo caso di tali varietà si presenta in P4: si tratta di una superficie e si deve a Severi l'aver provato che l'unica superficie liscia, non linearmente normale di P4, è una superficie di grado 4, proiezione della cosiddetta ‛superficie di Veronese' di P5. Sorprendente è la circostanza che di varietà di Severi ne esistono pochissime, cioè solo quattro tipi, di cui tre classicamente noti e uno scoperto da Lazarsfeld a seguito della segnalazione del risultato di Zak (v. Lazarsfeld e Van de Ven, 1984).
I metodi algebrici e la teoria degli schemi sono stati particolarmente incisivi in geometria numerativa, sì da rivoluzionarne completamente l'assetto. Ciò non è stato casuale, dato che proprio in questo settore della geometria algebrica, più che in altri, si erano rese evidenti le carenze tecniche dei metodi classici: basti ricordare le lunghe polemiche tra Severi e van der Waerden proprio sui fondamenti della geometria numerativa. Non è qui possibile menzionare i tanti importanti risultati classici ritrovati in modo rigoroso con i metodi moderni e le nuove possibilità che questi hanno aperto all'indagine dei geometri algebrici in questo settore. È forse opportuno segnalare invece che, negli ultimi anni, nuove idee, provenienti dalla fisica, stanno facendo luce su alcuni problemi classici insoluti, che neanche i nuovi metodi erano finora riusciti a scalfire. Queste nuove idee si possono compendiare in quelle, fra loro correlate, di simmetria speculare (mirror symmetry) e di coomologia quantica (quantum cohomology), motivate da teorie fisiche quali la teoria delle stringhe e la teoria quantistica dei campi. La teoria delle superstringhe suggerisce che la parte compatta della varietà spazio-tempo sia una varietà complessa compatta liscia X, di dimensione tre, tale che KX sia banale. Queste varietà si dicono varietà di Calabi-Yau, e la loro completa classificazione e descrizione è tuttora un problema aperto in geometria algebrica. I problemi numerativi nascono dalla constatazione che, in generale, su una siffatta varietà X vi sono soltanto un numero finito di curve razionali con data classe di omologia, e dunque si pone la questione di contare il numero di tali curve, questione che ha interesse fisico. Il primo problema di questo tipo fu affrontato classicamente da Schubert (v., 1879), il quale conta in 2875 il numero delle rette che appartengono a una ipersuperficie quintica generale di P4, che è appunto il più semplice esempio di varietà tridimensionale di Calabi-Yau. La soluzione del problema generale di contare il numero delle curve razionali di dato grado su una ipersuperficie quintica generale di P4, suggerita dall'idea fisica della esistenza della simmetria speculare, è stato risolto solo di recente da M. Kontsevich (v., 1995). Un problema analogo è quello del calcolo del numero delle curve razionali di dato grado d del piano passanti per 3d - 1 punti generali dello stesso piano: infatti, è facile verificare che tali curve dipendono da 3d - 1 parametri e quindi ne passano un numero finito per 3d - 1 punti sufficientemente generali. Anche questa questione è stata risolta da Kontsevich e Manin (v., 1994) usando la coomologia quantica. In sostanza si definisce, per certe varietà come il piano, un anello di coomologia più generale di quello usuale, nel quale la moltiplicazione conserva traccia dei numeri di curve razionali che verificano certe proprietà quali, per il piano, il passaggio per un dato numero di punti, ecc. Questo nuovo anello risulta essere associativo, e l'associatività produce delle formule ricorsive per il calcolo delle curve razionali in questione.
Vanno ancora citati alcuni recentissimi sviluppi sulle singolarità. A. J. De Jong (v., 1995) ha dimostrato che, data una varietà proiettiva X definita su un campo qualunque k, ne esiste un'alterazione (X′, f), cioè esistono una varietà proiettiva liscia X′ definita sullo stesso campo k e un morfismo suriettivo f:X′ → X. Un'alterazione è meno di una risoluzione delle singolarità, ma ha il pregio di esistere anche se k ha caratteristica positiva e, per molte questioni, può di fatto sostituire la risoluzione. È notevole il fatto che la dimostrazione di De Jong utilizzi in modo assai innovativo nello studio delle singolarità l'esistenza dello spazio dei moduli delle curve stabili.
Non è possibile concludere questa rassegna senza menzionare i formidabili progressi degli ultimi anni in geometria aritmetica, dovuti all'applicazione in teoria dei numeri di metodi, idee e tecniche algebrico-geometriche (v. numeri, teoria dei, vol. IV; v. Shafarevich, cap. 5); ad esempio, G. Faltings ha dimostrato la congettura di Mordell che afferma che su ogni curva algebrica di genere g ≥ 2 definita sul campo ℚ dei numeri razionali esiste un numero finito di punti a coordinate razionali (v. Mordell, 1969). La congettura di Mordell è stata ora generalizzata alle varietà di dimensione superiore da E. Bombieri (v., 1990), S. Lang (v., 1991) e P. Vojta (v., 1993) nel modo seguente: se X è una varietà di tipo generale definita su ℚ, esiste una sottovarietà Y di X di dimensione minore di quella di X, tale che c'è un numero finito di punti a coordinate razionali in X - Y.
Un altro spettacolare recente risultato è la dimostrazione del famoso ‛ultimo teorema di Fermat': per ogni n ≥ 3 l'equazione xn + yn = zn non ha soluzioni razionali non banali. Questo teorema è stato dimostrato da R. Taylor e A. Wiles (v., 1995; v. Wiles, 1995) provando una congettura di Shimura-Taniyama-Weil (v. Shimura, 1971). Una delle possibili formulazioni di questa congettura è che, se E è una curva ellittica definita su ℚ, esiste una certa curva X0 (N) e un morfismo non costante f:X0 (N) → E. La curva X0 (N) è una cosiddetta curva modulare. In breve, si tratta di una compattificazione naturale della curva Y0 (N) = H/Γ0 (N), dove Γ0 (N) è il sottogruppo di SL(2), formato dalle matrici
tali che N divide c. Qui N è il ‛conduttore' di E, ossia è il prodotto dei numeri primi p tali che la riduzione modulo p di E è singolare. Taylor e Wiles provano la congettura non per tutte le curve ellittiche, ma solo per certe curve ellittiche, dette ‛semistabili'. L'applicazione al teorema di Fermat procede, in breve, in questo modo: se si hanno interi a, b, c tali che an + bn = cn, si definisce la curva ellittica E di equazione affine y2 = x (x - an) (x + bn). Essa risulta allora avere conduttore N = 2 ed è semistabile; ciò darebbe luogo a un morfismo non costante f:X0 (2) → E, il che è assurdo perchè X0 (2) risulta essere razionale.
BIBLIOGRAFIA
Albanese, G., Trasformazione birazionale di una superficie algebrica qualunque in un'altra priva di punti multipli, in ‟Rendiconti del Circolo Matematico di Palermo", 1924, XLVIII, pp. 321-332.
Arbarello, E., De Concini, C., On a set of equations characterizing Riemann matrices, in ‟Annals of mathematics", 1984, CXX, 2, pp. 119-140.
Arbarello, E., Sernesi, E., The equation of a plane curve, in ‟Duke mathematical journal", 1979, XLVI, pp. 469-485.
Bagnera, C., de Franchis, M., Le superficie le quali ammettono una rappresentazione parametrica mediante funzioni iperellittiche di due argomenti, in ‟Rendiconti della Accademia nazionale delle scienze detta dei XL. Parte I: Memorie di matematica", 1908, XV, pp. 251-343.
Barth, W., Larsen, M. F., On the omotopy groups of complex projective algebraic manifolds, in ‟Mathematica scandinavica", 1972, XXX, pp. 88-94.
Bloch, S., Lectures on algebraic cycles, Durham, N. C., 1980.
Bloch, S., Kas, A., Lieberman, D., Zero cycles and a theorem of Roitman, in ‟Compositio mathematica", 1976, XXXIII, pp. 135-145.
Bombieri, E., Canonical models of surfaces of general type, in ‟Publications mathématiques de l'Institut des Hautes Études Scientifiques", 1971, XLII, pp. 35-87.
Bombieri, E., The Mordell conjecture revisited, in ‟Annali della Scuola Normale Superiore di Pisa" (Classe di scienze), 1990, XVII, 2, pp. 615-664.
Brill, A., Noether, M., Über die algebraische Funktionen und die Anwendung in der Geometrie, ‟Mathematische Annalen", 1873, VII, pp. 209-313.
Castelnuovo, G., Sulla razionalità delle involuzioni piane, in ‟Mathematische Annalen", 1894, XLIV, pp. 125-155.
Catanese, F., On the moduli spaces of surfaces of general type, in ‟Journal of differential geometry", 1984, XIX, pp 483-515.
Chang, M., Ran, Z., Unirationality of the moduli spaces of curves of genus 11, 13 (and 12), in ‟Inventiones mathematicae", 1984, LXXVI, pp. 41-54.
Chevalley, C., Les classes d'équivalence rationelle, in Anneaux de Chow et applications. Séminaire C. Chevalley, Paris 1958, articoli nn. 2, pp. 1-14, e 3, pp. 1-18.
Clebsch, A., Gordan, P., Theorie der Abelschen Functionen, Leipzig 1866.
Clemens, H., Griffiths, P., The intermediate jacobian of the cubic threefold, in ‟Annals of mathematics", 1972, XCV, pp. 281-365.
Cremona, L., Mémoire de géometrie pure sur les surfaces de troisième ordre, in ‟Journal für Mathematik", 1868, LXVIII, pp. 1-133.
Dedekind, R., Gesammelte mathematische Werke, vol. I, Braunschweig 1930.
De Jong, A. J., Smoothness, semi-stability and alterations, University of Utrecht, pre-print n. 916, 1995.
Deligne, P., La conjecture de Weil, I, in ‟Publications mathématiques de l'Institut des Hautes Études Scientifiques", 1974, XLIII, pp. 273-307.
Deligne, P., Mumford, D., The irreducibility of the space of curves of given genus, in ‟Publications mathématiques de l'Institut des Hautes Études Scientifiques", 1969, XXXVI, pp. 75-110.
Donaldson, S. K., Irrationality and the h-conordism conjecture, in ‟Journal of differential geometry", 1987, XXVI, pp. 141-168.
Dwork, B., On the rationality of the zeta function of an algebraic variety, in ‟American journal of mathematics", 1960, LXXXII, pp. 631-648.
Eisenbud, D., Harris, J., Limit linear series, the irrationality of Mg and other applications, in ‟Bulletin of the American Mathematical Society", 1984, X, pp. 277-286.
Ellingsrud, G., Peskine, C., Sur les surfaces lisses de P4, in ‟Inventiones mathematicae", 1989, XCV, pp. 1-12.
Enriques, F., Ricerche di geometria sulle superficie algebriche, in ‟Memorie della Reale Accademia delle Scienze di Torino", 1893, XLIV, 2, pp. 171-232.
Enriques, F., Introduzione alla geometria sopra le superficie algebriche, in ‟Rendiconti della Accademia nazionale delle scienze detta dei XL. Parte I: Memorie di matematica", 1896, X, 3, pp. 1-81.
Enriques, F., Sulle irrazionalità da cui può dipendere la risoluzione di un'equazione algebrica f(xyz) = 0 mediante funzioni razionali di due parametri, in ‟Mathematische Annalen", 1897, IL, pp. 1-23.
Enriques, F., Sopra un'involuzione non razionale dello spazio, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1912, XXI, 5, pp. 81-83.
Enriques, F., Sulla classificazione delle superficie algebriche e particolarmente sulle superficie di genere lineare p(1) = 1, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1914, XXIII, pp. 119, 206-214 e 291-297.
Enriques, F., Le superficie algebriche, Bologna 1949.
Enriques, F., Severi, F., Mémoire sur les surfaces hyperellyptiques, in ‟Acta mathematica", 1909-1910, XXXII-XXXIII, pp. 283-292 e 321-403.
Fano, G., Sopra alcune varietà algebriche a tre dimensioni aventi tutti i generi nulli, in ‟Atti della Reale Accademia delle Scienze di Torino", 1907-1908, XLIII, pp. 973-984.
Fano, G., Sulle varietà algebriche a tre dimensioni a superficie sezioni razionali, in Scritti matematici offerti a E. d'Ovidio, Torino 1918, pp. 342-363.
Franchetta, A., Sul sistema aggiunto ad una curva riducibile, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1949, VI, pp. 685-687.
Freedman, M., The topology of 4-manifolds, in ‟Journal of differential geometry", 1982, XVII, pp. 357-454.
Gieseker, D., Stable curves and special divisors, in ‟Inventiones mathematicae", 1982, LXVI, pp. 251-275.
Green, M., Koszul cohomology and the geometry of projective varieties, in ‟Duke mathematical journal", 1982, IL, 4, pp. 1087-1113.
Griffiths, P., Harris, J., On the variety of special linear systems on a general curve, in ‟Duke mathematical journal", 1980, XLVII, pp. 233-272.
Grothendieck, A., Le schéma de Hilbert, in ‟Séminaire Bourbaki", 1960-1961, exposé n. 221.
Grothendieck, A., Formule de Lefschetz et rationalité des fonctions L, in ‟Séminaire Bourbaki", 1964-1965, exposé n. 279.
Grothendieck, A., Standard conjectures on algebraic cycles, in Algebraic geometry, Oxford 1969, pp. 193-199.
Grothendieck, A., Dieudonné, J. A., Éléments de géométrie algébrique, Berlin-New York 19712.
Grothendieck, A. e altri, Séminaire de géométrie algébrique, 7 voll., Amsterdam-Heidelberg 1968-1977.
Harer, J., The second homology group of the mapping class group of an orientable surface, in ‟Inventiones mathematicae", 1983, LXXII, pp. 221-239.
Harer, J., Zagier, D., The Euler characteristic of the moduli space of curves, in ‟Inventiones mathematicae", 1986, LXXXV, pp. 457-485.
Harris, J., On the Kodaira dimension of the moduli space of curves II: the even genus case, in ‟Inventiones mathematicae", 1984, LXXV, pp. 437-466.
Harris, J., On the Severi problem, in ‟Inventiones mathematicae", 1986, LXXXIV, pp. 445-461.
Harris, J., Mumford, D., On the Kodaira dimension of the moduli space of curves, in ‟Inventiones mathematicae", 1982, LXVII, pp. 23-86.
Hartshorne, R., Varieties of small codimension in projective space, in ‟Bulletin of the American Mathematical Society", 1974, LXXX, pp. 1017-1032.
Hironaka, H., On resolution of singularities (characteristic zero), in Proceedings of the International congress of mathematicians, Stockholm 1962, pp. 507-521.
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero, in ‟Annals of mathematics", 1964, LXXIX, I, pp. 109-123 e II, pp. 205-326.
Hirzebruch, F., Neue topologische Methoden in der algebraischen Geometrie, Berlin 1956.
Hodge, W. D., The theory and applications of harmonic integrals, Cambridge 1941.
Iskohvskih, V. A., Fano 3-folds. I, in ‟Mathematics of the USSR. Izvestiya", 1977, XI, pp. 485-527.
Iskohvskih, V. A., Fano 3-folds. II, in ‟Mathematics of the USSR. Izvestiya", 1978, XII, pp. 496-506.
Iskohvskih, V. A., Birational automorphisms of three-dimensional algebraic varieties, in ‟Problems of contemporary mathematics", 1979, XII, pp. 159-236.
Kawamata, Y., A generalization of Kodaira-Ramanujam's vanishing theorem, in ‟Mathematische Annalen", 1982, CCLXI, pp. 43-46.
Kempf, G., Schubert methods with an application to algebraic curves, Amsterdam 1971.
Kleiman, S., Laksov, D., On the existence of special divisors, in ‟American journal of mathematics", 1972, XCIV, pp. 431-436.
Klein, F., Über Riemannsche Theorie der algebraischen Funktionen, Leipzig 1882.
Kodaira, K., On the theorem of Riemann-Roch for the adjoint systems on Kählerian varieties, in ‟Proceedings of the National Academy of Sciences", 1952, XXXVIII, pp. 522-527.
Kodaira, K., Collected works, 3 voll., Princeton, N. J., 1975.
Kontsevich, M., Enumeration of rational curves via torus actions, in The moduli space of curves (a cura di R. Dijkgraaf, C. Faber, G. van der Geer), Boston 1995, pp. 335-368.
Kontsevich, M., Manin, J., Gromow-Witten classes, quantum cohomology, and enumerative geometry, in ‟Communications in mathematical physics", 1994, CLXIV, pp. 525-562.
Lang, S. (a cura di), Number theory III: diophantine geometry, Berlin-New York 1991.
Lazarsfeld, R., Van de Ven, A., Topics in the geometry of projective space: recent work of F. L. Zak, Basel 1984.
Lefschetz, S., On certain numerical invariants of algebraic varieties with applications to abelian varieties, in ‟Transactions of the American Mathematical Society", 1921, XXII, pp. 327-428.
Miyaoka, Y., On the Chern numbers of surfaces of general type, in ‟Inventiones mathematicae", 1977, XLII, pp. 225-237.
Mordell, L. J., Diophantine equations, London 1969.
Mori, S., Classification of higher-dimensional varieties, in ‟Proceedings of symposia in pure mathematics", 1985, XLVI, 1, pp. 269-332.
Mori, S., Mukai, S., Classification of Fano 3-folds with B2≥ 2, in ‟Manuscripta mathematica", 1981, XXXVI, pp. 147-162.
Morin, U., Sulla classificazione proiettiva delle varietà algebriche a superficie sezioni razionali, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1939, VI, 18, pp. 147-171.
Morrow, J., Kodaira, K., Complex manifolds, New York 1971.
Mumford, D., Lectures on curves on an algebraic surface, Princeton, N. J., 1966.
Mumford, D., Rational equivalence of 0-cycles on surfaces, in ‟Journal of mathematics", 1969, IX, pp. 195-201.
Mumford, D., Towards an enumerative geometry of the moduli space of curves, Basel 1983.
Mumford, D., Fogarty, J., Geometric invariant theory, Berlin-New York 1982.
Noether, M., Über Flächen, welche Scharen rationaler Kurven besitzen, in ‟Mathematische Annalen", 1871, III, pp. 161-227.
Persson, U., On Chern invariants of surfaces of general type, in ‟Compositio mathematica", 1981, XLIII, pp. 3-58.
Picard, É., Mémoire sur la théorie des fonctions algébriques de deux variables indépendantes, in ‟Journal des mathématiques pures et appliquées", 1889, pp. 135-319.
Picard, É., Simart, G., Théorie des fonctions algébriques de deux variables indépendantes, 2 voll., Paris 1897-1906.
Poincaré, H., Sur les courbes tracées sur les surfaces algébriques, in ‟Annales de l'École normale supérieure", 1910, III, 27.
Ramanujam, C. P., Remarks on the Kodaira vanishing theorem, in ‟Journal of the Indian Mathematical Society", 1972, vol. XXXVI, pp. 41-51; e 1974, XXXVIII, pp. 121-124.
Rham, G. de, Variétés différentiables: formes, courants, formes harmoniques, Paris 1955.
Riemann, B., Theorie der Abel'schen Functionen, in ‟Journal für die reine und angewandte Mathematik", 1857, LIV, pp. 115-155.
Roitman, A. A., Rational equivalence of zero-cycles on surfaces, in ‟Mathematics of the USSR. Sbornik", 1972, XVIII, pp. 571-588.
Roitman, A. A., The torsion of the group of O-cycles modulo rational equivalence, in ‟Annals of mathematics", 1980, CXI, pp. 553-569.
Saint-Donat, B., On Petri's analysis of the linear system of quadrics through canonical curve, in ‟Mathematische Annalen", 1973, CCVI, pp. 157-175.
Samuel, P., Rational equivalence of arbitrary cycles, in ‟American journal of mathematics", 1956, LXXVIII, pp. 383-400.
Schubert, H., Kalkül der abzählenden Geometrie, Leipzig 1879.
Sernesi, E., L'unirazionalità dei moduli delle curve di genere dodici, in ‟Annali della Scuola Normale Superiore di Pisa" (Classe di Scienze), 1981, VIII, 4, pp. 405-439.
Serre, J. P., Faisceaux algébriques cohérents, in ‟Annals of mathematics", 1955, LXI, pp. 197-278.
Severi, F., Una proprietà delle forme algebriche prive di punti multipli, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1906, XI-XV, 5, pp. 691-696.
Severi, F., Sulla classificazione delle curve algebriche e sul teorema d'esistenza di Riemann, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1915, CCXLI, pp. 877-888 e 1011-1020; rist. con introduzione di S. L. Kleiman, Heidelberg 1979.
Severi, F., Vorlesungen über algebraische Geometrie: Geometrie auf einer Kurve, Riemannsche Flächen, Abelsche Integrale, Leipzig 1921.
Severi, F., La base per le varietà algebriche di dimensione qualunque contenute in una data e la teoria generale delle corrispondenze fra i punti di due superficie algebriche, in ‟Memorie della Reale Accademia d'Italia", 1934, V, pp. 239-283.
Severi, F., Il teorema di Riemann-Roch per curve, superficie e varietà; questioni collegate, Berlino 1958.
Shafarevich, I. R., Algebraic surfaces, Providence, R. I., 1967.
Shimura, G., Introduction to the arithmetic theory of automorphic functions, Princeton, N. J., 1971.
Shokurov, V. V., Smoothness of the general anticanonical divisor on a Fano 3-fold, in ‟Mathematics of the USSR. Izvestiya", 1980, XIV, pp. 395-405.
Shokurov, V. V., The existence of a straight line on Fano 3-folds, in ‟Mathematics of the USSR. Izvestiya", 1980, XV, pp. 173-209.
Taylor, R., Wiles, A., Ring theoretic properties of certain Hecke algebras, in ‟Annals of mathematics", 1995, CXLI, 2, pp. 553-572.
Teichmüller, O., Veränderliche Riemannsche Flächen, in ‟Deutsche Mathematik", 1944, VII, pp. 344-359.
Torelli, R., Sulle varietà di Jacobi, in ‟Atti dell'Accademia Nazionale dei Lincei: Rendiconti della Classe di scienze fisiche, matematiche e naturali", 1913, XXII, 5, pp. 98-103 e 437-441.
Vieweg, E., Vanishing theorems, in ‟Journal für die reine und angewandte Mathematik", 1982, CCCXXXV, pp. 1-8.
Vojta, P., Applications of arithmetic algebraic geometry to diophantine approximations, in Arithmetic algebraic geometry; lectures given at the 2nd session of the Centro Internazionale Matematico Estivo, Trento, June 24-July 2, 1991 (di J.-L. Colliot-Thélène, K. Kato e P. Vojta), Heidelberg 1993, pp. 164-208.
Waerden, B. L. van der, Einfürung in die algebraische Geometrie, Berlin 1939.
Walker, R. J., Reduction of the singularities of an algebraic surface, in ‟Annals of mathematics", 1935, XXXVI, pp. 336-365.
Weil, A., Foundations of algebraic geometry, New York 1947.
Weil, A., Number of solutions of equations over finite fields, in ‟Bulletin of the American Mathematical Society", 1949, LV, pp. 497-508.
Weil, A., Sur les courbes algébriques et les variétés qui s'en déduisent, Paris 1949.
Wiles, A., Modular elliptic curves and Fermat's last theorem, in ‟Annals of mathematics", 1995, CXLI, 2, pp. 443-551.
Witten, E., Monopoles and four-manifolds, in ‟Mathematical research letters", 1994, I, pp. 769-796.
Yau, S.-T., Calabi conjecture and some new results in algebraic geometry, in ‟Proceedings of the National Academy of Sciences", 1977, LXXIV, pp. 1798-1799.
Zak, F. L., Projections of varieties, in ‟Mathematics of the USSR. Sbornik", 1983, XLIV, pp. 535-544.
Zak, F. L., Severi varieties, in ‟Mathematics of the USSR. Sbornik", 1986, LIV, pp. 113-127.
Zariski, O., On the problem of existence of algebraic functions of two variables possessing a given branch curve, in ‟American journal of mathematics", 1929, LI, pp. 305-328.
Zariski, O., Algebraic surfaces, Berlin 1935.
Zariski, O., Reduction of the singularities of an algebraic 3-dimensional variety, in ‟Annals of mathematics", 1944, XLV, pp. 472-542.
Zariski, O., The connectedness theorem for birational transformations, in Proceedings of a Symposium in honor of S. Lefschetz, Princeton, N. J., 1955.
Concetti fondamentali di Igor R. Shafarevich
Sommario: 1. Introduzione. 2. Oggetti e strumenti principali: a) problemi fondamentali; b) principali strumenti. 3. Teoria generale: a) topologia delle varietà algebriche; b) proprietà dei divisori e varietà abeliane; c) applicazioni razionali e birazionali. 4. Curve, superfici, n-varietà: a) curve algebriche; b) superfici algebriche; c) varietà di dimensione ≥ 3; d) varietà astratte e analitiche complesse. 5. Applicazioni: teoria dei numeri, fisica teorica e teoria dei codici. □ Bibliografia.
1. Introduzione
La geometria algebrica è un naturale sviluppo della geometria analitica. Essa studia i sottoinsiemi dello spazio a un numero qualunque di dimensioni, definiti da equazioni polinomiali. Tali sottoinsiemi sono detti ‛varietà algebriche'.
Il confine tra geometria analitica e geometria algebrica si attraversa probabilmente quando si passa dallo studio delle coniche a quello delle curve di grado 3. Ciò è stato fatto già nell'antichità: Diofanto (III secolo d. C.) ha studiato le equazioni di grado 3 con due variabili e ha usato alcune trasformazioni che, con terminologia moderna, coincidono con la duplicazione di un punto di una curva cubica considerata come varietà abeliana. Questo è stato il punto di partenza degli studi di P. Fermat (XVII secolo) e di L. Eulero (XVIII secolo); quest'ultimo ha considerato anche gli integrali ellittici, cioè le forme differenziali sulla curva cubica. N. H. Abel, in un articolo del 1826, ha generalizzato tutto ciò a curve algebriche qualunque: egli ha considerato i divisori, la nozione di equivalenza tra questi e la nozione di genere.
Nell'Ottocento sono emerse due tendenze, con molte interazioni tra loro, ma ancora ben chiaramente distinguibili. La prima, di carattere più analitico, fa uso di funzioni analitiche, equazioni differenziali alle derivate parziali e talvolta di specifici suggerimenti provenienti dalla fisica. Tale tendenza, che ha avuto inizio con due articoli pubblicati da B. Riemann nel 1851 e nel 1857, è stata continuata da F. Klein (specialmente nelle sue lezioni del 1891-1892) e da H. Weyl (v., 1913). In questo contesto è stata creata la teoria delle varietà analitiche complesse di dimensione 1. Nel caso di dimensione superiore, un notevole impulso è stato dato dal lavoro di W. Hodge (articoli del periodo 1930-1950) e di K. Kodaira (articoli del periodo 1950-1970). Attualmente i loro continuatori sono i matematici e i fisici che lavorano sulle relazioni tra la geometria algebrica e la teoria quantistica dei campi.
La seconda tendenza è quella geometrico-sintetica, inaugurata da A. Clebsch (lavori del periodo 1863-1872) e sviluppata da M. Noether (lavori del periodo 1870-1890). Gli studiosi di geometria che hanno seguito questo approccio hanno sviluppato la teoria geometrica delle curve algebriche e introdotto alcune fondamentali nozioni per le varietà di dimensione superiore. Probabilmente il successo più rilevante mai ottenuto in geometria algebrica si deve al lavoro, effettuato tra la fine del XIX secolo e la prima metà del XX, dalla scuola italiana: G. Castelnuovo, F. Enriques, F. Severi e i loro allievi. Essi hanno creato quasi tutta la teoria delle superfici algebriche e le loro idee si sono finora dimostrate fondamentali anche in dimensione più alta.
Dopo il 1950, i lavori di A. Weil, J. P. Serre e A. Grothendieck, operando una nuova compenetrazione di idee topologiche, analitiche, algebriche e geometriche, hanno dato una forma completamente nuova alla geometria algebrica. Probabilmente, ciò che ha determinato i progressi più importanti è stata l'idea che i gruppi di omologia potessero definirsi in modo puramente algebrico per le varietà algebriche; tale idea risale ad alcuni lavori di teoria dei numeri di Weil. Finalmente, gli ultimi trent'anni hanno visto un nuovo potente avanzamento della disciplina e alcuni vecchi problemi, considerati come assai difficili perfino dai maestri della scuola italiana, sono stati finalmente risolti: ad esempio, l'esistenza della risoluzione delle singolarità provata da H. Hironaka (v. cap. 3, § c) e il fatto che la varietà Mg è di tipo generale per g abbastanza grande, risultato provato da J. Harris e D. Mumford (v. cap. 4, § a). La classificazione delle 3-varietà usando le contrazioni e la teoria dei raggi estremali è lavoro che risale agli ultimi quindici anni, e si deve soprattutto all'apporto di S. Mori (v. cap. 4, § c). In ogni modo, i problemi che si presentano in geometria algebrica sono ben lungi dall'essere definitivamente risolti. Si sa ben poco sulle varietà di codimensione maggiore di 1, sugli spazi di moduli delle superfici algebriche o sulla struttura delle varietà più interessanti ai fini della classificazione, quelle con κ = - ∞ o 0.
2. Oggetti e strumenti principali
a) Problemi fondamentali.
Lo spazio ambiente considerato in generale, è per lo più lo spazio proiettivo N-dimensionale PN (ℂ) con coordinate complesse. In tal caso le equazioni debbono essere omogenee, sicché le coordinate (x0, x1, ..., xN) e (λ x0, λ x1, ... , λ xN), λ ≠ 0, di uno stesso punto sono soluzioni delle stesse equazioni. Le varietà in questione sono dette ‛proiettive'. Se X e Y sono varietà proiettive, l'insieme X - Y è detto ‛varietà quasiproiettiva'. Il motivo per cui si sceglie di lavorare nello spazio proiettivo è che in esso le proprietà di intersezione sono più uniformi: ad esempio, nella geometria analitica due rette distinte nel piano affine si intersecano usualmente in un punto, ma talvolta possono essere parallele; nel piano proiettivo, invece, si intersecano sempre in un punto. Si sceglie poi di lavorare coi numeri complessi per la stessa ragione: già dall'algebra sappiamo che un'equazione polinomiale di grado n ha n radici, pur di considerare anche le radici complesse. Si noti che le radici dell'equazione f (x) = 0 sono i punti di intersezione delle curve algebriche y = f (x) e y = 0. Inoltre, come spazio topologico PN (ℂ) è compatto, mentre lo spazio affine non lo è. Tuttavia, le sottovarietà algebriche dello spazio affine, chiamate ‛varietà affini', sono spesso molto utili. Lo spazio proiettivo con coordinate (x0 x1, ..., xN) è ricoperto da sottospazi affini Aj, xj ≠ 0, con coordinate affini yj = xj / xi e ogni varietà proiettiva X dà luogo a varietà affini Uj = X ⋂ Aj che sono dette ‛carte affini' di X.
Una varietà proiettiva si dice ‛riducibile' se è l'unione di due varietà diverse dalla varietà stessa; in caso contrario, è detta ‛irriducibile'. Ogni varietà è l'unione finita di varietà irriducibili, X = ⋃ Xi, con Xi ≠ Xj, i ≠ j, dette ‛componenti irriducibili' di X. Tale decomposizione è unica.
Sia X ⊂ PN una varietà proiettiva. Un punto x ∈ X è detto ‛semplice' se per qualche sottospazio Pn ⊂ PN e per qualche proiezione PN → Pn esiste un intorno di x in X su cui la proiezione induce un omeomorfismo con un aperto di Pn. Se ciò accade per qualche proiezione, allora accade per la ‛generica' proiezione. Un punto che non sia semplice si dice ‛singolare'. Per esempio, la curva y2 = x2 + x3 in P2 (ℂ) interseca se stessa nell'origine (0, 0) e dunque questo punto è un suo punto singolare. Se tutti i punti della varietà sono semplici, la varietà si dice ‛liscia'. Una varietà liscia è una varietà analitica complessa. I punti singolari di una varietà irriducibile formano una varietà algebrica Sing (X) diversa da X. Per tutti i punti semplici il numero n dianzi introdotto è lo stesso, ed è detto ‛dimensione (algebrica)' di X: n = dim X. Per una varietà irriducibile X e una sottovarietà Y ⊂ X differente da X si ha dim Y 〈 dim X, e dim X - dim Y, detta ‛codimensione di Y in X′, si scrive codim Y. Le varietà algebriche di dimensione 1 sono dette ‛curve', quelle di dimensione 2 ‛superfici', quelle di dimensione 3 sono dette ‛3-varietà'. La dimensione di X come spazio topologico è il doppio della sua dimensione algebrica.
Sia U una delle carte affini della varietà proiettiva irriducibile X, con coordinate y1, ..., yN. Una funzione razionale f =
in queste coordinate, con g e h polinomi, h non identicamente nullo su U, è detta ‛funzione razionale' su X. Questa nozione evidentemente non dipende dalla scelta di U. Le funzioni razionali su X formano un campo ℂ (X). Una funzione razionale f è detta ‛regolare' nel punto x ∈ X se si può scrivere come
con h (x) ≠ 0. Un'applicazione di una varietà proiettiva in un'altra definita da funzioni razionali è detta ‛applicazione razionale': essa si dice regolare nel punto x se può essere definita da funzioni regolari in x; se essa è regolare in tutti i punti della varietà, allora viene chiamata semplicemente applicazione regolare. Dunque si hanno due tipi di applicazioni in geometria algebrica: le applicazioni razionali e quelle regolari. Le applicazioni razionali possono non essere definite ovunque. Ma per ogni applicazione razionale f definita su una varietà X, esiste una sottovarietà Y ⊂ X diversa da X tale che f è regolare in tutti i punti di X - Y. Entrambi i tipi di applicazioni danno luogo in modo ovvio a una nozione di isomorfismo: gli isomorfismi così ottenuti sono detti, rispettivamente, isomorfismo birazionale e semplicemente isomorfismo. Due varietà algebriche irriducibili X e X′ sono birazionalmente isomorfe se e solo se vi sono delle sottovarietà Y ⊂ X e Y′ ⊂ X′ di dimensione più bassa, tali che X - Y e X′ - Y′ siano isomorfe.
Corrispondentemente, vi sono due problemi principali in geometria algebrica: la classificazione delle varietà algebriche a meno di isomorfismo birazionale o a meno di isomorfismo. Due varietà X e Y sono birazionalmente isomorfe se e solo se i loro campi delle funzioni razionali ℂ (X) e ℂ (Y) sono isomorfi su ℂ . Uno dei principali invarianti birazionali di una varietà è la dimensione: essa è uguale al grado di trascendenza (v. algebra, vol. I) di ℂ (X) su ℂ. Le varietà birazionalmente isomorfe allo spazio proiettivo sono dette ‛razionali'. Ciò equivale a dire che il campo delle funzioni razionali ℂ (X) è isomorfo al campo ℂ (t1, ..., tn) delle funzioni razionali in n variabili indipendenti. Si pone così l'importante ‛problema della razionalità': come si fa a determinare quando una varietà è razionale per mezzo dei suoi invarianti geometrici?
b) Principali strumenti.
Si studia una varietà algebrica X studiandone le sottovarietà Y ⊂ X. Quelle più semplici sono le sottovarietà di codimensione 1. Ad esempio, per una varietà definita da una singola equazione in PN tutte le componenti irriducibili hanno codimesione 1. Tali sottovarietà di PN sono dette ‛ipersuperfici'. In generale, tutte le componenti irriducibili dell'intersezione di una varietà irriducibile X con un'ipersuperficie che non la contenga hanno codimensione 1 in X. Il contrario è vero, ma solo localmente e solo per le varietà lisce. Per ogni varietà liscia X, data una sottovarietà irriducibile Y ⊂ X di codimensione 1 e un punto x ∈ Y, esiste una funzione razionale f regolare in x tale che Y è definita dall'equazione f = 0 in un intorno di x. Questa funzione può essere scelta in modo, per così dire, minimale, cioè in modo tale che per ogni funzione razionale u regolare in x si abbia u = fr v per qualche intero r ≥ 0, con v regolare in x e non identicamente nulla su Y. Ogni funzione razionale è quoziente di due funzioni regolari in x, e dunque una rappresentazione di questo tipo esiste per ogni funzione razionale, ma con r ∈ ℤ. Benché la scelta di f non sia per nulla unica, il numero r è indipendente dalla scelta di f e del punto x. Se r > 0, l'intero r è detto ‛ordine di zero' di f lungo Y; se r 〈 0, allora - r è l'‛ordine di polo'.
Per una data funzione non nulla f, il numero r è diverso da zero solo per un numero finito di sottovarietà irriducibili, Yi, i = 1, ..., m. Se ri sono i numeri corrispondenti, si scrive (f) = r1 Y1 + r2 Y2 + ... + rm Ym. Questa espressione viene detta ‛divisore corrispondente alla funzione f′. In generale, un divisore è una combinazione lineare formale a coefficienti interi di sottovarietà irriducibili di codimensione 1. I divisori formano in modo naturale un gruppo Div (X). I divisori del tipo (f) formano un sottogruppo P (X) ⊂ Div (X), in quanto (f) + (g) = (fg). Si pone Div (X)/P (x) = Cl (X). Due divisori D1 e D2 sono detti equivalenti se D1 - D2 = (f) per qualche f. Ciò significa che essi determinano lo stesso elemento in Cl (X). Il gruppo Cl (X) è l'invariante più importante di una varietà. Per esempio Cl (P1) = ℤ, e questo esprime la circostanza che il numero dei poli di una funzione razionale non nulla sulla sfera di Riemann eguaglia il numero degli zeri e che esiste una funzione razionale con zeri e poli assegnati, purché questi soddisfino la suddetta proprietà. Ogni applicazione regolare suriettiva f : X → Y dà luogo a un omomorfismo f*: Cl (Y) → Cl (X). In particolare, il gruppo Cl (X) è invariante per isomorfismi.
Un divisore D = r1 Y1 + r2 Y2 + ... + rm Ym si dice ‛effettivo' e si scrive D ≥ 0, se ri ≥ 0 per ogni i = 1, ..., m. Dato un divisore D, l'insieme di tutte le funzioni razionali f tali che (f) + D ≥ 0 è chiaramente uno spazio vettoriale, denotato con L (D). Se D ≥ 0, dire che f ∈ L (D) equivale a dire che f è regolare fuori di Y1, ..., Ym e che gli ordini di polo di f lungo le sottovarietà Yi sono limitati dagli interi ri. Un teorema fondamentale afferma che per le varietà proiettive la dimensione di L (D) è finita: essa si denota col simbolo l (D). Si ha sempre l (0) = 1. Ciò significa che le sole funzioni razionali senza poli sono le costanti, dal che segue che una funzione f è determinata dal suo divisore (f) a meno di un fattore costante.
Supponiamo che l (D) = m > 0 e sia f0, f1, ..., fm-1 una base di L (D). Possiamo definire un'applicazione razionale della varietà X nello spazio proiettivo Pm-1 nel modo seguente: x → (0 (x), f1 (x), ..., fm-1 (x)). Se si cambia la base f0, f1, ..., fm-1 di L (D), l'applicazione cambia soltanto per una trasformazione proiettiva dello spazio Pm-1. Dunque, l'applicazione è essenzialmente determinata dal divisore D ed è denotata col simbolo ϕD. Essa dipende soltanto dalla classe di equivalenza del divisore D e, di fatto, tutte le applicazioni razionali si possono ottenere in questo modo. La nozione di applicazione razionale definita a partire da una classe di equivalenza di un divisore è particolarmente utile in quanto ogni varietà liscia determina intrinsecamente e in modo univoco una ben precisa classe di equivalenza e questa a sua volta dà luogo a una ben determinata applicazione razionale definita sulla varietà. Questa classe è correlata alle forme differenziali sulla varietà (v. geometria differenziale, vol. X).
Consideriamo le forme differenziali olomorfe di massima dimensione n = dim X su X. Per ogni punto x ∈ X vi sono n funzioni razionali z1, z2, ..., zn regolari in x, che definiscono un omeomorfismo di qualche intorno di x su un aperto di ℂn. Una forma differenziale ω si dice ‛forma algebrica regolare' se nell'intorno di ogni punto x si può scrivere nella forma ω = f dz1 ⋀ dz2 ⋀ ... ⋀ dzn, dove f è una funzione razionale regolare in x. Una ‛forma differenziale razionale' su una varietà liscia X è definita come una forma differenziale algebrica regolare su qualche varietà quasiproiettiva X - Y, dove Y è una sottovarietà di dimensione più piccola di quella di X. Allora anche nell'intorno di un punto x ∈ Y, la forma ω si può scrivere nello stesso modo ω = f dz1 ⋀ dz2 ⋀ ... ⋀ dzn, con f funzione razionale. Se ω = g du1 ⋀ du2 ⋀ ... ⋀ dun è la rappresentazione della stessa forma in un diverso aperto, allora si ha g = f det
Da ciò segue che i divisori definiti dall'equazione f = 0 nell'intorno di ciascun punto x, dove f è dedotta dalla rappresentazione di una forma ω non nulla nell'intorno di x, si incollano e definiscono un unico divisore su X, che si denota col simbolo (ω). Ovviamente, date due forme ω1 e ω2, si ha ω1 = f ω2, con f funzione razionale non nulla, e si ha (ω1) = (f) + (ω2). Dunque, tutti i divisori del tipo (ω) sono equivalenti e definiscono la stessa classe in Cl (X), che è detta ‛classe canonica' di X e si denota con KX o semplicemente con K.
I numeri l (nKX) = Pn, per ogni n > 0, sono detti ‛plurigeneri' di X e P1 è detto ‛genere geometrico'. È facile vedere che i Pn sono invarianti per isomorfismi birazionali. Se l (nK) > 0, l'applicazione razionale ϕnK è detta ‛n-sima applicazione pluricanonica'. La sua immagine ϕnK (X), o meglio, la sua chiusura, è detta ‛n-simo modello canonico' Xn di X. Essa è definita univocamente da X e n, a meno di trasformazioni proiettive. Se Pn > 0 per almeno un n > 0, si definisce un invariante κ = max {dim Xn, Pn > 0}, detto ‛dimensione canonica' di X. Se Pn = 0 per ogni n > 0, si pone κ = - ∞.
Se κ ≠ - ∞ si hanno diversi modelli canonici, ma un'importante congettura afferma che vi è tra di loro il seguente legame: vi è un intero r > 0 tale che, per ogni m > 0, i modelli canonici Xmr sono tutti isomorfi. Ciò è equivalente a un enunciato di tipo algebrico: l'anello ⊕ L (nK), con l'ovvia operazione di moltiplicazione, ha un numero finito di generatori. Pertanto, tale congettura è detta la congettura della generazione finita. Se si suppone che la congettura sia vera, si ha un modello canonico essenzialmente unico I (X), detto ‛varietà di Iitaka' di X, e inoltre dim I (X) = κ e vi è un'unica applicazione razionale f : X → I (X). Se κ = dim X, allora I (X) è birazionalmente isomorfo a X, e in tal caso si dice che X è una varietà di tipo generale. Poiché I (X) è unico a meno di trasformazioni proiettive, la considerazione delle varietà di Iitaka riconduce la classificazione birazionale delle varietà di tipo generale alla classificazione proiettiva. D'altra parte, se 0 〈 κ 〈 dim X, allora X è ‛fibrata' dalle varietà f-1 (x), x ∈ I (X), di dimensione minore dim X - κ, e si può sperare di poter applicare qualche argomento induttivo. Dunque, appare chiaro che i casi ‛essenziali' sono κ = dim X (varietà di tipo generale), κ = 0 e κ = - ∞. Al momento attuale, la congettura di finita generazione è stata dimostrata per dim X ≤ 3 e per le varietà di tipo generale in dimensione qualunque.
3. Teoria generale
a) Topologia delle varietà algebriche.
Ogni varietà algebrica, in quanto sottoinsieme di uno spazio proiettivo complesso, è anche uno spazio topologico. Una varietà proiettiva è compatta, una varietà algebrica irriducibile è connessa. Ogni varietà algebrica si può triangolare. Una varietà algebrica liscia X ha un'orientazione naturale, e ciò è conseguenza del fatto che localmente X è come ℂn e ℂn ha un'orientazione naturale, tale che, per ogni base e1, ..., en di ℂn su ℂ, la base e1, ..., en, ie1, ..., ien di ℂn su ℝ ha orientazione positiva; è facile vedere che la definizione non dipende dalla scelta della base e1, ..., en. Sia Y una sottovarietà irriducibile k-dimensionale di una varietà algebrica liscia X. Si può effettuare una triangolazione di X tale che Y - Sing (Y) consista di simplessi. Usando l'orientazione naturale di Y - Sing (Y) si possono orientare i simplessi di questo spazio. In tal modo si associa a Y una catena Y di dimensione 2k che, di fatto, è un ciclo il quale determina un elemento del gruppo H2k (X, ℤ) che si denota col simbolo [Y] o semplicemente con Y. Per esempio, data una curva algebrica X, si ha H2 (X, ℤ) = ℤ e per ogni divisore D = r1 P1 + ... + rm Pm si ha [D] = r1 + ... + rm, intero che si denota col simbolo deg (D). Per una varietà proiettiva liscia X, si ha KX = - c1, dove c1 è la prima classe di Chern di X (v. geometria differenziale, vol. III).
Sia f una funzione razionale non nulla su una varietà proiettiva liscia e irriducibile X, e sia (f) = E1 - E2, con E1 > 0, E2 > 0 ed E1, E2 senza divisori in comune. Si pone E1 = (f)0, E2 = (f)∞. Per ogni costante c, poniamo Dc = (f - c)0. Scegliamo un cammino 1-dimensionale γ che, sulla sfera di Riemann, congiunge 0 con ∞. Allora i divisori Dc, con c ∈ γ, formano una catena con bordo E1 - E2, sicché (f) è sempre omologo a 0. Per una curva proiettiva questo implica che il numero degli zeri di una funzione razionale è uguale al numero dei poli. Per varietà proiettive lisce qualunque si vede che l'applicazione Div (X) → H2n-2 (X, ℤ) è un omomorfismo e che i divisori principali stanno nel suo nucleo. Dunque si ha un omomorfismo Cl (X) → H2n-2 (X, ℤ), la cui immagine, detta ‛gruppo di Severi' di X, si denota col simbolo SX.
Sia X una varietà algebrica liscia e ne siano Y e Z sottovarietà tali che dim Y + dim Z = dim X, Y e Z si intersecano in un numero finito di punti semplici sia su Y che su Z e, in ciascuno di questi punti, gli spazi tangenti a Y e a Z si intersecano solo nell'origine. L'indice di intersezione topologico (Y.Z) eguaglia il numero dei punti di intersezione contati con molteplicità + 1 o - 1. Dall'esistenza di un'orientazione naturale segue immediatamente che nel nostro caso queste molteplicità sono tutte + 1 e dunque l'indice di intersezione è uguale al numero dei punti di intersezione.
Sia X una varietà proiettiva di dimensione n in PN. Poiché H2n (PN, ℤ) = [L] ℤ, dove L è un sottospazio lineare n-dimensionale, si ha X = d [L] in H2n (PN, ℤ) per qualche intero d. Si può scegliere un sottospazio lineare M di dimensione N - n che interseca X trasversalmente. Ne segue che (X.M) = d e quindi d > 0. L'intero d è detto ‛grado' di X. Per esempio, il grado di un'ipersuperficie determinata da un polinomio irriducibile è uguale al grado del polinomio. Ora, se X e Y sono curve proiettive irriducibili in P2 di gradi m e n, allora X = mL, Y = nL e (X.Y) = m.n (L.L) = m.n (due rette si intersecano in un punto!). Questo risultato non è altro che il teorema di Bézout: il numero dei punti di intersezione di due curve eguaglia il prodotto dei loro gradi (se esse si intersecano trasversalmente; altrimenti i punti di intersezione devono essere contati con molteplicità come le radici multiple dei polinomi). Esso rappresenta solo il più semplice esempio di proprietà di intersezione di varietà algebriche che può essere dedotto in questo modo.
Come abbiamo detto, ogni varietà algebrica liscia è anche una varietà analitica complessa. Una varietà proiettiva eredita dallo spazio proiettivo ambiente una metrica kähleriana ed è dunque una varietà di Kähler (v. geometria differenziale, vol. X). In particolare, la sua coomologia possiede la decomposizione
Ogni divisore determina una classe di omologia [D] ∈ H2n-2 (X, ℂ) e, per dualità di Poincaré, una classe in H2 (X, ℂ). È facile vedere che, nella decomposizione di cui sopra, la classe corrispondente a un divisore appartiene a H1,1 (X, ℂ). Ciò caratterizza le classi corrispondenti ai divisori, cioè il sottogruppo SX di H2n-2 (X, ℂ). Resta aperto il problema di vedere se un fatto analogo valga anche per sottovarietà di codimensione più alta, almeno per H2k (X, ℚ) (congettura di Hodge). K. Kodaira ha dimostrato che le varietà proiettive lisce sono caratterizzate tra tutte le varietà kähleriane dalla proprietà che la classe di tipo (1, 1) corrispondente alla metrica kähleriana è intera (v. geometria differenziale, vol. X).
b) Proprietà dei divisori e varietà abeliane.
L'omomorfismo h : Cl (X) → H2n-2 (X, ℤ) ha per immagine il gruppo di Severi, SX, che è un sottogruppo abeliano finitamente generato e dunque dà luogo a un invariante di natura discreta. Al contrario, il nucleo Cl0 (X) di h appare essere ‛naturalmente' parametrizzato dai punti di una varietà proiettiva liscia e irriducibile. Per comprendere il significato di questa affermazione è opportuno premettere la definizione di varietà abeliana. In generale, una biiezione tra gli elementi di un gruppo astratto e i punti di una varietà proiettiva liscia A induce una struttura di gruppo anche sui punti di A. Siano A × A → A e A → A le applicazioni che definiscono la moltiplicazione e il passaggio all'inverso di un elemento nel gruppo. È naturale assumere che entrambe queste applicazioni siano applicazioni regolari di varietà algebriche: le varietà proiettive che hanno questa proprietà sono dette varietà abeliane. Si può provare che esse sono sempre commutative; ciò è ovvio nel caso di Cl0 (X). Dire che esiste una parametrizzazione ‛naturale' di Cl0 (X) significa dire che esiste una varietà abeliana, che si denota con Pic0 (X), e un divisore D sul prodotto X × Pic0 (X) con la seguente proprietà. Siano p1 e p2 le proiezioni di D sul primo e sul secondo fattore di X × Pic0 (X). Si scelga un punto a0 in Pic0 (X). Allora si vede facilmente che, per ogni a ∈ Pic0 (X), la classe di p1 (p2-1 (a) - p2-1 (a0)) sta in Cl0 (X). La proprietà basilare è che l'applicazione a → [p1 (p2-1 (a) - p2-1 (a0))] è un isomorfismo tra Pic0 (X) e Cl0 (X). Questa proprietà caratterizza univocamente Pic0 (X), che è detta ‛varietà di Picard' di X. La sua dimensione è uguale alla dimensione q dello spazio delle 1-forme regolari su X. Inoltre, b1 = 2 q, dove b1 è il primo numero di Betti di X.
Ogni varietà abeliana A è un toro complesso. Ciò significa che il suo rivestimento universale è isomorfo, come gruppo, a ℂn con n = dim A, e A stesso è isomorfo a ℂn / L, dove L è un reticolo in ℂn, cioè un sottogruppo generato da 2n vettori linearmente indipendenti su ℝ. Tuttavia, non ogni toro complesso è una varietà abeliana, ossia non è detto che si possa immergere in uno spazio proiettivo. Le condizioni necessarie e sufficienti affinché ciò accada sono di questo tipo. Sia A = ℂn / L e sia Ω una matrice di tipo (n, 2 n) le cui colonne sono date dalle coordinate dei vettori di una base di L; allora deve esistere una matrice T antisimmetrica a coefficenti interi di tipo (2n, 2n) tale che ΩTΩt = 0 e iΩTΩ*> 0, dove t indica la trasposizione, * la trasposizione hermitiana, mentre col simbolo > 0 si indica che la matrice hermitiana è definita positiva. La matrice Ω non è univocamente determinata da L, ma può essere moltiplicata a sinistra per una matrice invertibile (n, n) a coefficienti complessi e a destra per una matrice invertibile (2n, 2n) a coefficienti interi. Usando queste trasformazioni si può porre Ω nella forma (E, U) - dove U è una matrice arbitraria e E la matrice unità - e T nella forma
dove D è la matrice diagonale D = (d1, ..., dn), in cui d1 divide d2 ... divide dn. Poniamo S = DU. Allora le precedenti condizioni prendono la forma St = S (cioè S è simmetrica) e Im S > 0, che significa che, se S = X + iY, con X e Y reali, allora Y è definita positiva. Tali matrici formano il cosiddetto ‛semipiano superiore di Siegel', che si denota con Hn. Se D = E, due matrici S′ e S definiscono varietà abeliane isomorfe se e solo se S′ = (A1 + SA3)-1 (A2 + SA4) dove
Tali trasformazioni formano il cosiddetto ‛gruppo simplettico intero' Γ. Nel caso D sia qualunque è ancora facile descrivere Γ. Dunque, in ogni caso tutte le varietà abeliane di dimensione n sono descritte, a meno di isomorfismi, da un invariante discreto D e uno continuo, cioè un punto dello spazio complesso Hn/Γ. In generale, parametri continui che definiscono le strutture di varietà algebriche sono detti ‛moduli' e, in particolare, Hn/Γ è lo spazio dei moduli delle varietà abeliane. Come spazio complesso Hn/Γ è isomorfo a una varietà quasi proiettiva.
c) Applicazioni razionali e birazionali.
Sia X una varietà quasiproiettiva. Una varietà liscia X′ e un'applicazione regolare f : X′ → X è detta ‛risoluzione delle singolarità' di X se f è un isomorfismo birazionale ed è un isomorfismo tra X - Sing (X) e f-1 (X - Sing (X)). H. Hironaka ha dimostrato che ogni varietà quasiproiettiva possiede una risoluzione delle singolarità.
Un isomorfismo birazionale f : X′ → X può non essere un isomorfismo, perché f o il suo inverso possono non essere regolari. Il caso più semplice è quello in cui f è regolare ma f-1 non lo è. Secondo un teorema dimostrato in una situazione più generale da O. Zariski, non si ha soltanto un'affermazione negativa di ‛non regolarità', ma in realtà la f realizza una specie di ‛chirurgia'. Cioè, se X è liscia e f-1 non è regolare, allora esiste una sottovarietà Z di codimensione 1 in X′ tale che f (Z) ha dimensione più piccola di quella di Z, ossia f ‛contrae' Z.
Vi sono alcuni tipi assai semplici di contrazioni, dette ‛dilatazioni' o ‛σ-processi'. Cioè, per ogni varietà liscia X e per ogni sottovarietà liscia C ⊂ X di codimensione m ≥ 2 esiste una varietà liscia X′ e un'applicazione regolare birazionale σ : X′ → X tale che σ-1 è regolare fuori di C, si ha σ (Z) = C con Z di codimensione 1 in X′ e per ogni c ∈ C la fibra σ-1 (c) è uno spazio proiettivo di dimensione m - 1. Per esempio, se X è una superficie e c ∈ X un punto, allora σ contrae una retta a c. In coordinate affini l'applicazione si può scrivere come (x, y) → (x, xy) ed essa evidentemente contrae la retta x = 0 al punto (0, 0). L'applicazione σ-1 non è regolare nei punti c ∈ C. Se ci si avvicina a c lungo una curva L trasversale a C, il limite di σ-1 (d), al tendere di d a c, dipende soltanto dalla retta tangente a L in c modulo TC, dove TC è lo spazio tangente a C in c. In tal modo si ottiene un isomorfismo tra σ-1 (c) e lo spazio proiettivo associato allo spazio lineare TX / TC.
Un altro teorema di Hironaka, detto ‛teorema dell'eliminazione dei punti di indeterminazione', asserisce che, per ogni applicazione razionale di varietà proiettive f : X → Y, esiste un'applicazione regolare s : X′ → X che è una composizione di un numero finito di dilatazioni, tale che l'applicazione h : X′ → Y, con h = f 0 s, è regolare. Nel caso delle curve lisce non vi sono dilatazioni e quindi ogni applicazione razionale definita su una curva liscia è regolare; in particolare, per le curve lisce proiettive gli isomorfismi birazionali coincidono con gli isomorfismi. Un'applicazione birazionale regolare tra superfici algebriche è una composizione di dilatazioni. Dunque, ogni applicazione birazionale tra superfici è prodotto di dilatazioni e di loro inverse. Non è noto se ciò sia vero anche per varietà di dimensione più alta.
Alcune proprietà importanti delle applicazioni razionali e birazionali definite su una varietà liscia proiettiva X sono correlate alle curve che appartengono a X e alle loro intersezioni con i divisori di date classi di equivalenza. Denotiamo con NE (X) il sottoinsieme di H2 (X, ℝ) = H2 (X, ℤ) ⊗ ℝche consiste di tutte le combinazioni lineari con coefficienti positivi delle classi corrispondenti a curve algebriche C ⊂ X. Naturalmente, si tratta di un cono convesso che è un nuovo invariante, molto importante, della varietà X. Sono particolarmente importanti gli elementi di NE (X) che corrispondono alle immagini di applicazioni birazionali di P1 in X, che sono dette ‛curve razionali'. Si prova che ogni applicazione birazionale regolare di X che non sia un isomorfismo, contrae a un punto qualche curva razionale C ⊂ X tale che (C.KX) 〈 0. Ciò giustifica l'interesse nelle curve C tali che (C.KX) 〈 0. Il numero di intersezione (C.KX) è ben definito giacché possiamo considerare C come un elemento di H2 (X, ℤ), e KX come elemento di H2n-2 (X, ℤ). È più facile lavorare con la chiusura ¯NE (X) di NE (X) in H2 (X, ℝ). Il sottoinsieme di -N--E- (X) definito dalla condizione (x.KX) 〈 0 viene denotato col simbolo -N--E- (X)-.
Una direzione di ricerca iniziata da Hironaka e sviluppata da Mori e altri ha condotto ai seguenti risultati. Il cono -N--E- (X)-, se non vuoto, è localmente poliedrale. Ciascuno dei suoi raggi estremali è generato da una classe corrispondente a una curva razionale C con 0 > (C.KX) ≥ - dim X - 1. Un raggio estremale ha un piano di supporto generato da un elemento in H2n-2 (X, ℤ) corrispondente a un divisore D tale che l'applicazione ϕmD sia regolare per qualche m > 0 e contragga a un punto esattamente le curve la cui classe in H2 (X, ℤ) appartiene al corrispondente raggio estremale. Comunque, l'immagine di ϕmD è in generale singolare.
4. Curve, superfici, n-varietà
a) Curve algebriche.
Una curva algebrica liscia proiettiva è, dal punto di vista topologico, una superficie orientabile compatta. Essa ha un solo invariante topologico, e cioè il genere g. Poiché tutte le curve lisce birazionalmente isomorfe sono isomorfe, il genere è un invariante birazionale. Nel caso delle curve, il teorema di Riemann-Roch (v. geometria, vol. III) prende la forma: l (D) + l (K - D) = deg (D) - g + 1. Se D = 0 otteniamo l (K) = g, cioè g uguaglia il genere geometrico. Per D = K otteniamo deg (K) = 2 g - 2. Per una curva algebrica liscia C, la condizione κ = - ∞ è equivalente a g = 0; in tal caso C è isomorfa alla retta proiettiva. La condizione κ = 0 equivale a g = 1; in tal caso C è una varietà abeliana di dimensione 1 (v. cap. 3, § b). Le curve con g = 1, dette ‛curve ellittiche', sono isomorfe a una curva liscia di grado 3 in P2. Il semipiano superiore di Siegel H1 è l'ordinario semipiano H e il gruppo simplettico Γ è l'ordinario gruppo modulare. Dunque, le curve ellittiche non isomorfe sono in corrispondenza biunivoca con i punti di H/Γ. La funzione j, detta ‛invariante modulare assoluto', determina un isomorfismo j : H/Γ → ℂ.
Il caso rimanente κ = 1 corrisponde a g > 1, e allora la curva è una varietà di tipo generale. Ciò significa che per n sufficientemente grande l'applicazione pluricanonica ϕnK è un isomorfismo con una curva C in uno spazio proiettivo PN. Qui si ha N = l (nK) - 1 e dal teorema di Riemann-Roch segue facilmente che l (nk) = (2 n - 1) (g - 1) se n ≥ 2. Il grado d della curva C eguaglia deg (D), dove D è l'intersezione con gli iperpiani di PN. Nel nostro caso D = nK, e quindi il grado di C è n (2 g - 2). Inoltre, dallo stesso teorema segue facilmente che è anche possibile prendere n = 3 affinché ϕnK sia un isomorfismo. Dunque la classificazione birazionale delle curve algebriche di genere g > 1 è equivalente alla classificazione, a meno di trasformazioni proiettive, delle curve 3-canoniche di grado 6 (g - 1) e genere g in PN, con N = 5 g - 4.
Già nel caso g = 1 abbiamo visto che queste curve sono descritte dai punti di una varietà algebrica. Nel caso generale di curve di genere g, diremo che una varietà Mg è uno spazio dei moduli per tali curve se esiste una corrispondenza biiettiva ‛naturale' ψ tra le classi di equivalenza birazionale di curve di genere g e i punti della varietà Mg. ‛Naturale' significa che se f : X → S è un'applicazione regolare di varietà algebriche tale che f-1 (s) è una curva liscia proiettiva di genere g per ogni s ∈ S, cioè se si ha una ‛famiglia' di curve algebriche parametrizzate da S, allora l'applicazione s → ψ (f-1 (s)) di S in Mg è regolare. Secondo un risultato basilare provato da Mumford, lo spazio dei moduli delle curve di genere g > 1 esiste ed è una varietà quasiproiettiva di dimensione 3 g - 3. La dimostrazione è basata sulla considerazione delle curve 3-canoniche di cui sopra e sul fatto che le curve di dato grado in uno spazio proiettivo si possono rappresentare con i punti di una varietà algebrica H (il che è possibile, più in generale, per varietà algebriche di dimensione qualunque), interpretando l'equivalenza proiettiva di curve in PN come l'azione del gruppo G delle trasformazioni proiettive di PN su H e costruendo la varietà quoziente H / G usando la teoria degli invarianti. P. Deligne e D. Mumford hanno dimostrato che la varietà Mg è irriducibile.
Un'altra strada, di tipo analitico, per studiare lo spazio Mg è quella proposta da O. Teichmüller; essa è basata sulla rappresentazione di Mg come quoziente Tg / Γ di un dominio limitato Tg ⊂ ℂ3g-3 per un gruppo discreto di automorfismi Γ (v. geometria, vol. III). La varietà Mg ha κ = - ∞ per g ≤ 12, ma è una varietà di tipo generale per g ≥ 24. Essa ha degli aspetti in comune con i quozienti di dominî omogenei limitati in ℂn per l'azione di gruppi discreti di tipo aritmetico. Per esempio, per la sua caratteristica di Eulero si ha e (Mg) =
dove B2g è il numero di Bernoulli, dunque un numero legato in modo naturale alla teoria dei numeri (J. Harer e D. Zagier). In questo caso e (Mg) è definito come nella teoria degli orbifold: se Mg = Tg / Γ e G è un sottogruppo di indice finito in Γ che agisce liberamente su Tg, allora e (Mg =
dove e (Tg / Γ) è la solita caratteristica di Eulero. In ogni caso Tg non è omogeneo: tutti i suoi automorfismi sono contenuti nel gruppo discreto Γ.
b) Superfici algebriche.
Per superficie intenderemo qui una superficie liscia e proiettiva. In questo caso incontriamo per la prima volta le dilatazioni. Se σ : X → Y è una dilatazione di una superficie, allora σ contrae una curva C a un punto e pertanto si ha rank SY = rank SX - 1 e X non è isomorfo a Y. Questo procedimento si può ripetere e si ottiene così, a differenza del caso delle curve, un numero infinito di superfici birazionialmente equivalenti ma a due a due non isomorfe: ... X2 → X1 → X → Y. Di conseguenza, ci imbattiamo qui in due problemi: descrivere gli isomorfismi birazionali tra superfici e classificare le classi di equivalenza birazionale delle superfici mediante i loro invarianti (ad esempio κ).
Se una superficie X ammette un'applicazione birazionale regolare X → Y, che non sia un isomorfismo, su una superficie Y allora rank SY 〈 rank SX. Dunque, si può procedere finché si ottiene una superficie per cui non esistono tali applicazioni: una superficie siffatta si dice ‛modello minimo'. Tutte le altre superfici sono ottenute da un modello minimo con una successione di dilatazioni; tuttavia, una superficie può a priori essere birazionalmente equivalente a molti diversi modelli minimi. Ciò dipende dalla classe canonica della superficie.
In generale, un divisore D su una varietà proiettiva liscia X si dice ‛numericamente effettivo' o, in breve, nef, se si ha (C.D) ≥ 0 per ogni curva C ⊂ X. Per varietà lisce proiettive di dimensione qualunque, due modelli minimi, le cui classi canoniche sono nef, sono isomorfi se sono birazionalmente equivalenti. Dunque, superfici X con KX nef hanno un unico modello minimo. Se KX non è nef, si può applicare la teoria descritta alla fine del cap. 3, § c. Si ha un raggio estremale generato da una curva razionale C con (C.KX) = - 3, - 2 o - 1. Nel primo caso, la corrispondente contrazione f manda tutto X in un punto e X è isomorfo a P2: la superficie è razionale. Nel secondo caso, la contrazione f manda X su una curva liscia E, f-1 (e) è isomorfo a P1 per ogni e ∈ E e X è birazionalmente isomorfo a E × P1. Queste superfici sono dette ‛rigate'. Nel terzo caso, la contrazione è una dilatazione. Ripetendo l'argomento possiamo escludere che avvenga questo caso. Quindi, le sole superfici che non hanno un unico modello minimo sono le superfici razionali e le rigate. Queste sono proprio le superfici con κ = - ∞, che sono caratterizzate dalla condizione Pm = 0 per ogni m > 0. Tuttavia, già la condizione P12 = 0 è sufficiente a caratterizzarle. Le superfici razionali sono caratterizzate dalle condizioni q = 0, P1 = P2 = 0.
Il caso in cui KX è nef coincide con il caso κ ≥ 0. Se κ = 0 si hanno, innanzi tutto, le superfici con KX = 0. Queste o sono superfici abeliane ovvero sono semplicemente connesse; nel secondo caso esse sono dette superfici K3. Le superfici K3 hanno uno spazio dei moduli che è quoziente di un dominio omogeneo 19-dimensionale per un gruppo discreto (per la descrizione delle varietà abeliane, v. cap. 3, § b). Tutte le altre superfici con κ = 0 sono ottenute da superfici abeliane o da K3 come quozienti per l'azione di un gruppo finito di automorfismi. Nel caso κ = 1 qualche applicazione pluricanonica f = ϕmK manda X su una curva C in modo che per tutti i punti c ∈ C, tranne al più un numero finito, la fibra f-1 (c) è una curva ellittica. Nel caso κ = 2 si hanno le superfici di tipo generale. Esse possono essere studiate in modo analogo a quello usato per le curve di genere g > 1 nel cap. 4, § a.
Si potrebbe sperare che l'invariante fondamentale κ si possa ricostruire dalla topologia della superficie algebrica, così come accade nel caso delle curve (κ = - ∞, 0, 1 a seconda che g = 0, 1, > 1). Ma non è così: esistono superfici algebriche omeomorfe con diversi invarianti κ. Per contro κ è determinato dalla struttura della superficie come 4-varietà differenziabile. Rimane aperto il problema di vedere se lo spazio dei moduli delle superfici di tipo generale che sono tra loro diffeomorfe è irriducibile, così come accade nel caso delle curve.
c) Varietà di dimensione ≥ 3?
In linea di principio, le considerazioni svolte nel precedente paragrafo per la teoria delle superfici algebriche possono essere applicate anche alle varietà di dimensione superiore. La difficoltà maggiore sta nel fatto che una contrazione trasforma una varietà liscia in una che può avere delle singolarità e, se si vuole ripetere il procedimento, si è obbligati a lavorare con varietà singolari. Dunque, il problema è quello di trovare una classe di singolarità tali che, su varietà con singolarità di questa classe, si possa sviluppare lo stesso macchinario di cui si dispone nel caso delle varietà lisce, e cioè esistenza della classe canonica, dell'indice di intersezione di curve con divisori, ecc. e validità dei principali teoremi sulle contrazioni, in modo che non sorgano i problemi indicati dianzi (cioè introduzione a mezzo di contrazioni di nuovi tipi di singolarità). Varietà siffatte sono state trovate e chiamate ‛varietà terminali'. In realtà, una contrazione può produrre varietà non terminali anche partendo da varietà terminali, ma sono stati individuati certi tipi di trasformazioni birazionali, detti flips, che riportano le suddette varietà nella classe delle varietà terminali. In linea di principio questo metodo può essere applicato a varietà di dimensione qualunque, e si spera che per tale applicazione le difficoltà da risolvere siano per lo più tecniche. Questa linea di indagine è detta ‛programma di Mori'.
Finora i risultati più precisi sono stati ottenuti per le 3-varietà. Essi includono la caratterizzazione delle 3-varietà (terminali) per cui la classe canonica non è nef, che coincidono con le 3-varietà con κ = - ∞. Per una 3-varietà proiettiva liscia si ha κ = - ∞ se e solo se essa è ‛ricoperta da curve razionali', il che significa che per ogni punto della varietà passa una curva razionale. Rimane da vedere se ciò valga anche in dimensione maggiore. Se la classe canonica è nef, si ha 0 ≤ κ ≤ 3. Nel caso κ = 0 non si sa quasi nulla. In dimensione ≤ 3 la congettura della generazione finita è stata provata, dunque si può parlare del modello di Iitaka I (X) (v. cap. 2, § b). Se κ = 1, allora I (X) è una curva liscia e, data l'applicazione f : X → I (X), le varietà f-1 (y) sono superfici lisce con κ = 0 per tutti gli y ∈ I (X), tranne al più un numero finito. Per κ = 2 la superficie I (X) può essere singolare. Per ogni y ∈ I (X) - C, dove C è un'opportuna curva su I (X), la varietà f-1 (y) è una curva ellittica. Nel caso κ = 3 si ha una varietà di tipo generale, l'applicazione f : X → I (X) è un isomorfismo birazionale e le singolarità di I (X) sono descritte.
d) Varietà astratte e analitiche complesse.
Varietà algebriche immerse in spazi proiettivi diversi possono essere isomorfe, e dunque è naturale ricercare una definizione di varietà algebrica che sia indipendente dalla sua immersione in uno spazio proiettivo, così come si ha una definizione degli spazi topologici o delle varietà differenziabili che non presuppone la loro immersione in ℝn. Tale definizione di ‛varietà astratta' è stata suggerita da A. Weil, J. P. Serre e A. Grothendieck. La nozione cui si perviene è in verità più generale, ossia vi sono varietà astratte che non sono isomorfe a varietà quasiproiettive. Per esempio, su una varietà astratta compatta possono esistere curve C (necessariamente riducibili) che, come cicli, sono omologhe a 0, mentre su una varietà quasiproiettiva questo è impossibile, perché C è una curva proiettiva e l'indice di intersezione (C.L) con la classe di un iperpiano L è positiva ed è uguale al grado di C. Ad ogni modo una varietà astratta è birazionalmente equivalente a una proiettiva.
Una varietà liscia (quasiproiettiva o astratta) è una varietà analitica complessa (v. geometria, vol. III). Nel caso delle varietà lisce compatte (in particolare di quelle proiettive) le loro proprietà come varietà algebriche e analitiche si accordano bene. Ad esempio, una funzione meromorfa su una varietà algebrica liscia e compatta è una funzione razionale, un'applicazione olomorfa coincide con un'applicazione regolare, in particolare l'isomorfismo, nel senso delle varietà analitiche o algebriche, coincide. Una sottovarietà analitica complessa di una varietà proiettiva è essa stessa una varietà proiettiva liscia. Per ogni varietà analitica complessa connessa e compatta X, il campo delle funzioni meromorfe M (X) è isomorfo al campo ???OUT-C??? (X0), con X0 varietà algebrica (possibilmente di dimensione inferiore a quella di X) determinata a meno di isomorfismi birazionali. Ogni curva complessa compatta (una superficie di Riemann) è isomorfa a una curva proiettiva (teorema di esistenza di Riemann).
Kodaira ha sviluppato una classificazione alquanto dettagliata delle superfici analitiche complesse compatte, che ricorda la classificazione delle superfici algebriche. Il ruolo dell'invariante κ è svolto qui dall'invariante a = dim X0, dove X0 è la varietà algebrica introdotta prima. Se il primo numero di Betti b1 della superficie è pari (come accade per le superfici proiettive dove b1 = 2 q), essa è una ‛deformazione' di una superficie algebrica, ed è altresì kähleriana. Le superfici con b1 dispari non sono neanche omeomorfe a superfici proiettive, e non si è ancora riusciti a descriverle completamente.
5. Applicazioni: teoria dei numeri, fisica teorica e teoria dei codici.
La geometria algebrica ha numerose applicazioni in differenti settori della matematica e in settori scientifici vicini. Le applicazioni che riguardano la teoria dei numeri, considerate forse le più rilevanti, sono apparse quando la geometria algebrica era ancora in uno stadio iniziale del suo sviluppo e l'hanno profondamente influenzata. Tali applicazioni sono possibili in quanto gran parte della geometria algebrica può essere sviluppata con metodi puramente algebrici per varietà algebriche definite da equazioni con coefficienti in un campo qualunque F (in breve: ‛definite su F′). Per esempio, gli indici di intersezione tra curve e divisori possono essere definiti senza ricorrere a considerazioni topologiche, così come in modo puramente algebrico si definiscono le molteplicità delle radici di un polinomio. Lo stesso vale per la teoria delle forme differenziali e della classe canonica. Ancora più sorprendente è il fatto che perfino i gruppi di (co)omologia (con opportuni coefficienti) si possano definire in modo puramente algebrico. Tutto ciò può essere applicato alle varietà algebriche definite su campi di interesse in teoria dei numeri. Ad esempio, per varietà definite su un campo finito Fp con p elementi, i loro punti con coordinate in Fp corrispondono a soluzioni di opportune congruenze. Citiamo uno dei risultati ottenuti in questa direzione: data una curva liscia e proiettiva di genere g definita sul campo Fp e detto N il numero dei punti con coordinate in Fp, si ha la disuguaglianza ∣N - (p + 1)∣ 〈 2 g √p. Questo risultato si può interpretare come l'analogo dell'ipotesi di Riemann sugli zeri della funzione δ. Risultati analoghi sono stati dimostrati per varietà algebriche di dimensione qualunque definite sul campo Fp.
Per varietà definite sul campo ℚ dei numeri razionali, la ricerca dei punti con coordinate in ℚ (in breve: ‛punti razionali') coincide con la teoria delle equazioni diofantee. Ad esempio, per le curve ellittiche definite su ℚ, la legge di gruppo della corrispondente varietà abeliana è anch'essa espressa da formule con coefficienti in ℚ, e dunque l'insieme dei punti razionali è un gruppo. L. Mordell ha dimostrato che questo gruppo ha un numero finito di generatori. Per una curva di genere g > 1 definita su ℚ, G. Faltings ha dimostrato che il numero dei suoi punti razionali è finito. Secondo una congettura di E. Bombieri e P. Vojta, questo fatto dovrebbe generalizzarsi nel seguente modo a varietà X di tipo generale e di dimensione qualunque: esiste una sottovarietà Y ⊂ X di dimensione minore di quella di X, tale che il numero dei punti razionali di X - Y è finito.
Vi è una gran mole di applicazioni della geometria algebrica alla fisica sviluppate in buona parte nell'ultimo decennio. Giusto per menzionare alcuni esempi, lo spazio dei moduli Mg delle curve di genere g svolge un ruolo fondamentale nella teoria delle stringhe. Per esempio, sia Λn il fibrato vettoriale (v. geometria differenziale, vol. X) la cui fibra su un punto x ∈ Mg è lo spazio L (nKC) per la curva C corrispondente al punto x, e sia λn = c1 (Λn): D. Mumford ha dimostrato che λn = (6 n (n - 1) + 1) λ1 e in particolare che λ2 = 13 λ1. Ciò sembra essere in relazione col fatto che 26 = 2 • 13 è la dimensione della varietà spazio-tempo della teoria delle stringhe. D'altro canto questa dimensione è 10 nella teoria delle superstringhe e ipoteticamente si può immaginare che la varietà spazio-tempo sia data da M4 × X, dove M4 è l'usuale varietà di Minkowski, mentre per X una sorta di supersimmetria suggerisce una struttura di 3-varietà complessa con KX = 0. La cosiddetta teoria nella simmetria speculare, inoltre, è in relazione col calcolo delle curve razionali di dato grado su certe 3-varietà X con KX = 0.
Vi sono poi sorprendenti applicazioni della geometria algebrica alla teoria dei codici. Dal punto di vista matematico, un codice è un sottospazio lineare di uno spazio vettoriale su un campo finito (usualmente su F2). I codici ‛migliori' tra quelli finora conosciuti sono stati costruiti prendendo come spazi lineari spazi del tipo L (D) con D divisori su curve algebriche alquanto esotiche definite su campi finiti.
BIBLIOGRAFIA
Barth, W., Peters, C., Van de Ven, A., Compact complex surfaces, Berlin-New York 1984.
Bers, L., Uniformization, moduli, Kleinian groups, in ‟The bulletin of the London Mathematical Society", 1972, IV, pp. 257-300.
Castelnuovo, G., Memorie scelte, Bologna 1937.
Clemens, C. H., Kollár, J., Mori, S. (a cura di), Higher dimensional complex geometry: a summer seminar at the University of Utah, Salt Lake City 1987, Paris 1988.
Cornell, G., Silverman, J. (a cura di), Arithmetic geometry, New York 1986.
Enriques, F., Memorie scelte di geometria, 3 voll., Bologna 1956-1966.
Enriques, F., Chisini, O., Lezioni sulla teoria geometrica delle equazioni e delle funzioni algebriche, 4 voll., Bologna 1915-1934.
Griffiths, P., Harris, J., Principles of algebraic geometry, New York 1978.
Grothendieck, A., Fondements de la géométrie algébrique, in ‟Séminaire Bourbaki", 1957-1962, exposés nn. 141, 149, 182, 190, 195, 212, 221, 232, 236, commentaires.
Harris, J., Mumford, D., On the Kodaira dimension of the moduli space of curves, in ‟Inventiones mathematicae", 1982, LXVII, pp. 23-86.
Hartshorne, R., Algebraic geometry, New York 1977.
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero, in ‟Annals of mathematics", 1964, LXXIX, pp. 109-326.
Lang, S. (a cura di), Number theory III: diophantine geometry, Berlin-New York 1991.
Mumford, D., Abelian varieties, London 1970.
Mumford, D., Fogarty, J., Geometric invariant theory, Berlin-New York 1982.
Severi, F., Lezioni di geometria algebrica, Padova 1908.
Severi, F., Opere matematiche, 6 voll., Roma 1971-1989.
Shafarevich, I. R., Osnovy algebraicheskoi geometrii, 2 voll., Moskva 1988 (tr. ingl.: Basic algebraic geometry, Berlin-New York 1994).
Siegel, C., Analytic functions of several complex variables, Princeton, N. J., 1948-1949.
Weil, A., Øuvres scientifiques-Collected papers, 3 voll., New York 1979.
Weyl, H., Die Idee der Riemannschen Fläche, Leipzig 1913.
© Istituto della Enciclopedia Italiana - Riproduzione riservata