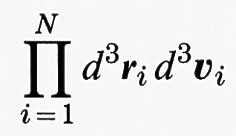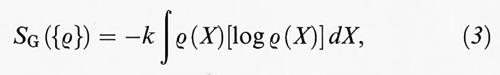Irreversibilita

Irreversibilità

Sommario: 1. Introduzione: a) considerazioni qualitative; b) considerazioni quantitative; c) teoria microscopica. 2. Il problema dell'irreversibilità macroscopica. 3. La risposta di Boltzmann. 4. L'uso della probabilità. 5. Condizioni iniziali. 6. Origine degli stati a bassa entropia. 7. Irreversibilità e stabilità macroscopica. 8. Confronto fra le entropie di Boltzmann e di Gibbs. 9. Osservazioni. 10. Conclusioni. □ Bibliografia.

1. Introduzione

Se si considera il successo dei metodi statistici introdotti da James Maxwell, William Thomson (che divenne più tardi lord Kelvin) e resi quantitativi da Ludwig Boltzmann - metodi che condussero alla spiegazione e alla predizione del comportamento dei sistemi macroscopici sulla base della dinamica microscopica reversibile - si resta sorpresi che ancor oggi regni tanta confusione sul problema dell'irreversibilità. A mio parere questa situazione deriva dal fatto che l'originalità di questi metodi ha reso assai difficile la loro comprensione profonda. La rilevanza che questi assunsero nella forma precisa ed elegante che Boltzmann diede loro con la sua famosa equazione cinetica e con il teorema H li rese facili bersagli di molti attacchi. La confusione creata da queste incomprensioni e dalle controversie che ne seguirono fra Boltzmann e alcuni dei suoi contemporanei, in particolare Ernst Zermelo, è stata perpetuata da vari autori che non compresero, o non spiegarono adeguatamente, le risposte del tutto soddisfacenti che Boltzmann aveva dato a questi problemi nelle sue repliche a coloro che lo attaccavano e negli scritti successivi. Questa incomprensione, vista la chiarezza di tali scritti, non ha alcuna scusante. Per usare le parole di Erwin Schrödinger, ‟le idee di Boltzmann conducono realmente a comprendere" le origini del comportamento macroscopico dei corpi materiali. Tutte le affermazioni sulla incompatibilità fra leggi microscopiche e comportamento macroscopico (almeno tutte quelle di cui sono a conoscenza) sono a mio avviso errate e non si vede alcuna necessità di cercare spiegazioni alternative, almeno per quanto riguarda il livello classico non relativistico. Per la loro grande chiarezza, oltre che per il loro fascino, suggeriamo qualche utile lettura, come alcune raccolte di scritti di Boltzmann e di suoi contemporanei (v. Brush, 1966 e 1976; v. Broda, 1955), e qualche articolo di autori più recenti (v. Feynman, 1965; v. Feynman e altri, 1963-1965; v. O. Penrose, 1970; v. R. Penrose, 1989; v. Ruelle, 1991; v. Lanford, 1981; v. Lebowitz, 1993); suggeriamo inoltre la lettura del bellissimo articolo di Thomson (v., 1875) dal quale è tratto il seguente brano: ‟Le equazioni del moto in dinamica astratta sono perfettamente reversibili; qualsiasi soluzione di queste equazioni rimane valida anche quando la variabile tempo, t, è sostituita da - t. I processi fisici, quali l'attrito dei solidi, la conduzione del calore e la diffusione, sono invece irreversibili. Ciò nonostante, il principio della dissipazione dell'energia è compatibile con una teoria molecolare in cui ogni particella sia soggetta alle leggi della dinamica astratta".

a) Considerazioni qualitative

La teoria statistica di Boltzmann sul comportamento fuori dall'equilibrio (asimmetrico rispetto al tempo e irreversibile) associa a ciascuno stato microscopico di un sistema macroscopico, sia esso un gas, un liquido o un solido, un numero S_B chiamato ‛entropia di Boltzmann' di tale stato (v. Penrose, 1970). Questa entropia coincide (a meno di termini trascurabili rispetto alle dimensioni del sistema) con l'entropia termodinamica macroscopica di Clausius se il sistema è in equilibrio, e in questo caso coincide anche con l'entropia di Gibbs S_G (per il significato di insiemi di Gibbs, limitatamente agli stati di equilibrio, v. meccanica statistica, vol. IV), che è definita non per i microstati individuali ma per gli insiemi statistici o distribuzioni di probabilità (in una maniera che descriveremo più avanti). Questo è vero anche per sistemi in equilibrio locale. Tuttavia, a differenza di S_G - che non cambia nel tempo anche per insiemi che descrivono sistemi (isolati) non in equilibrio, per esempio fluidi che si evolvono secondo le equazioni dell'idrodinamica - S_B cresce generalmente in una maniera che spiega e descrive qualitativamente l'evoluzione verso l'equilibrio dei sistemi macroscopici.

Questo comportamento di S_B è dovuto alla separazione fra le scale microscopiche e macroscopiche, cioè al numero molto grande di gradi di libertà che intervengono nella specificazione delle proprietà macroscopiche. È proprio tale separazione fra le scale che permette di fare previsioni precise sull'evoluzione di una realizzazione individuale tipica di un sistema macroscopico, il cui comportamento, in realtà, è irreversibile. Come è stato detto succintamente da Maxwell (v., 1872), ‟la seconda legge della termodinamica deriva dalla nostra esperienza che si fonda sul comportamento di corpi formati da un numero immenso di molecole; tuttavia, essa è continuamente violata [...] quando si tratti di un gruppo sufficientemente piccolo di molecole [...]. Quando tale numero [...] aumenta [...] la probabilità di una variazione misurabile [...] può considerarsi praticamente come impossibile". I vari insiemi usati comunemente in meccanica statistica devono essere considerati soltanto come strumenti matematici per descrivere un comportamento che è praticamente identico per ‛quasi tutti' i singoli sistemi macroscopici nell'insieme. Per quanto questi strumenti siano estremamente utili e alcuni dei teoremi che li coinvolgono siano molto eleganti, essi non vanno confusi con ciò che realmente avviene in un singolo sistema, il che equivarrebbe a confondere le immagini con la realtà. Inoltre, il comportamento asimmetrico nel tempo che si manifesta nella singola evoluzione tipica di un sistema macroscopico distingue l'irreversibilità macroscopica da quel tipo di evoluzione mescolante degli insiemi che si manifesta anche nel comportamento caotico di sistemi che hanno solo un piccolo numero di gradi di libertà, come ad esempio due sfere rigide in una scatola. Chiamare irreversibile questo tipo di dinamica è pertanto fonte di confusione.

b) Considerazioni quantitative

Gli aspetti qualitativi essenziali del comportamento macroscopico possono essere compresi sulla base della incompressibilità del flusso nello spazio delle fasi rappresentato dalle equazioni di Hamilton. Questi aspetti non dipendono dal fatto che siano verificate rigorosamente alcune ipotesi quali la positività degli esponenti di Ljapunov, dell'ergodicità, del mescolamento (mixing) o di ‛eguali probabilità a priori', ma sono tuttavia importanti per una descrizione quantitativa dell'evoluzione macroscopica che è data, in molti casi, da equazioni autonome di tipo idrodinamico asimmetriche rispetto al tempo. Tali equazioni possono essere dedotte (in alcuni casi rigorosamente) da una dinamica microscopica reversibile scalando opportunamente le unità macro- e microscopiche di spazio e di tempo e facendo poi tendere all'infinito il rapporto fra le scale macro- e microscopiche (v. Lebowitz e altri, 1988; v. De Masi e Presutti, 1991; v. Spohn, 1991). (Questi limiti esprimono in forma matematica la situazione fisica determinata dal fatto che il rapporto fra le scale macro- e microscopiche è enorme). Usando la legge dei grandi numeri si può allora dimostrare che queste equazioni descrivono il comportamento di quasi tutti i sistemi individuali nell'insieme e non soltanto quello delle medie sull'insieme; ciò significa che la dispersione tende a zero nel limite sulle scale. Descrizioni di questo tipo rimangono valide, e risultano estremamente accurate, anche quando il rapporto macro/micro è finito ma molto grande; esse sono tuttavia inapplicabili quando il sistema contiene soltanto poche particelle.

L'esistenza e la forma di tali equazioni idrodinamiche dipendono dalla natura della dinamica microscopica. In particolare, le instabilità delle traiettorie dovute a una dinamica microscopica caotica hanno un ruolo importante nel determinare molti aspetti dell'evoluzione macroscopica. Ciò si può mostrare in dettaglio col semplice esempio del gas di Lorentz, che consiste di un numero grandissimo di particelle non interagenti che si muovono in un reticolo periodico di diffusori fissi convessi situati su di un piano in modo tale che una particella possa percorrere una distanza massima tra due collisioni. La natura caotica della dinamica microscopica, che conduce a una distribuzione locale approssimativamente isotropa delle velocità, è la causa diretta dell'esistenza di una semplice descrizione autonoma deterministica (data da un'equazione di diffusione) dei profili tipici della densità macroscopica di tale sistema. Un altro esempio è la descrizione attraverso l'equazione di Boltzmann della densità nello spazio a sei dimensioni della posizione e della velocità di un sistema macroscopico di bassa densità di sfere rigide (v. Lanford, 1981; v. Lebowitz e altri, 1988; v. Spohn, 1991; v. De Masi e Presutti, 1991). Questi esempi, nonostante siano forniti da modelli molto semplificati, sono utili in quanto suscettibili di una trattazione matematica rigorosa in ogni dettaglio. Essi mostrano immediatamente, e in modo da riuscire a convincere anche (come disse Mark Kac) gli ‟irragionevoli", non soltanto per il fatto che non esiste alcun conflitto tra il comportamento reversibile microscopico e quello irreversibile macroscopico, ma anche perché il secondo deriva dal primo in praticamente tutti i casi in cui gli stati iniziali microscopici siano compatibili con un dato stato macroscopico di non equilibrio, in completo accordo con le idee di Boltzmann.

c) Teoria microscopica

È chiaro che Boltzmann analizzò il problema servendosi della meccanica classica newtoniana e in questo articolo ci porremo nella stessa prospettiva. La situazione è sotto molti aspetti simile anche in meccanica quantistica, dove il flusso incompressibile e reversibile nello spazio delle fasi è sostituito da un'evoluzione unitaria in uno spazio di Hilbert. In particolare, non crediamo che il processo di misura quantistica sia una nuova sorgente di irreversibilità e pensiamo che con tali affermazioni si ponga in effetti il carro davanti ai buoi. Misurazioni reali sui sistemi quantistici sono asimmetriche rispetto al tempo poiché implicano necessariamente sistemi con un numero molto grande di gradi di libertà la cui irreversibilità può essere compresa attraverso un'estensione naturale delle idee classiche (v. Aharonov e altri, 1964; v. Dürr e altri, 1992; v. Page, 1993).

Esistono tuttavia anche alcuni aspetti genuinamente nuovi della meccanica quantistica, che sono rilevanti per il nostro problema. Anzitutto, per seguire direttamente l'analogia classica si dovrebbe associare uno stato macroscopico a una funzione d'onda arbitraria del sistema, il che è impossibile, come si deduce chiaramente dal paradigma (o paradosso) del gatto di Schrödinger (v. Bell, 1987). In secondo luogo, le correlazioni quantistiche fra sistemi separati che nascono dalla sovrapposizione delle funzioni d'onda rendono in generale impossibile assegnare una funzione d'onda a un sottosistema S₁ di un sistema S in uno stato definito ψ anche quando non vi sia interazione diretta tra S₁ e il resto di S; ciò rende il concetto di sistema isolato assai più problematico in meccanica quantistica che non nella teoria classica. Questi aspetti della meccanica quantistica richiedono un'analisi accurata per comprendere in che modo essi influenzino l'irreversibilità che si osserva nel mondo reale. Una discussione approfondita di questi aspetti non soltanto va al di là delle finalità di questo articolo, ma richiederebbe idee nuove e un lavoro notevole che ancora non è stato fatto, anche se il problema è stato affrontato da diversi punti di vista (v. Aharonov e altri, 1964; v. Bell, 1987; v. Page, 1993; v. Dürr e altri, 1992; v. Halliwell e altri, 1994).

In questo articolo trascureremo completamente anche la relatività speciale e generale. Il fenomeno che vogliamo spiegare, cioè il comportamento asimmetrico nel tempo di oggetti macroscopici localizzati spazialmente, ha certo molti aspetti che sono simili nell'universo relativistico (reale) e nell'universo (modello) non relativistico. Non tenteremo dunque neppure di toccare i seri problemi concettuali che riguardano la natura dello spazio e del tempo, che recentemente sono stati discussi ampiamente in relazione alla reversibilità nella radiazione dei buchi neri e nella loro evaporazione (v. Halliwell e altri, 1994). Questi problemi vanno al di là della competenza dell'autore e del resto sembra probabile che la loro soluzione richieda l'introduzione di concetti nuovi. Concentreremo invece la nostra attenzione sul problema dell'origine dell'irreversibilità macroscopica nel contesto del modello classico più semplice; la soluzione di questo problema, data da Maxwell, Thomson e Boltzmann, a nostro avviso rimane valida, essenzialmente immutata, anche nel caso dei sistemi reali.

2. Il problema dell'irreversibilità macroscopica

Consideriamo un sistema macroscopico che si evolva nel tempo come quello rappresentato schematicamente in fig. 1 dalle immagini di un sistema binario, poniamo due inchiostri di diverso colore. Le quattro immagini della figura rappresentano le concentrazioni locali dei due componenti a tempi diversi. Supponiamo di sapere che il sistema è stato isolato durante tutto il tempo in cui sono state riprese le immagini e supponiamo ci si chieda di identificare l'ordine temporale in cui le immagini sono state riprese. La risposta ovvia, basata sull'esperienza, è che il tempo aumenta andando dalla fig. 1A alla fig. 1D. Ci piacerebbe poter dimostrare che questa risposta discende direttamente dalle leggi microscopiche della natura, ma non è così, perché secondo le leggi microscopiche che conosciamo se è permessa la sequenza che va da A verso D lo è anche quella che va da D verso A.

Ciò si vede facilmente nella meccanica classica, dove lo stato microscopico di un sistema isolato classico di N particelle è rappresentato da un punto X = (r₁, v₁, r₂, v₂, ..., r_N, v_N) nello spazio delle fasi Γ, dove r_i e v_i sono la posizione e la velocità della i-esima particella. Chiaramente, le immagini della fig. 1 non specificano in maniera completa il microstato X del sistema; ciascuna figura fornisce una descrizione grossolana di X che denoteremo con M (X) e chiameremo macrostato corrispondente a X. Per esempio, se supponiamo che ciascuna immagine della fig. 1 rappresenti un litro di liquido, ognuno potrebbe essere suddiviso in un miliardo di piccoli cubi, e allora il macrostato M specificherebbe semplicemente (entro un certo errore) la frazione di particelle di ciascun tipo in ogni cubo j, j = 1, ..., 10⁹. A ciascun macrostato M corrisponde un gran numero di microstati contenuti in una regione Γ_M nello spazio delle fasi Γ. Per specificare adeguatamente la regione Γ_M occorre conoscere anche l'energia totale E nonché ogni altra costante del moto macroscopicamente rilevante, per esempio additiva (anch'essa entro un certo margine di errore). Benché una tale specificazione dello stato macroscopico contenga evidentemente elementi di una certa arbitrarietà, questo per ora non ci deve preoccupare. Tutte le affermazioni qualitative che faremo sull'evoluzione nel tempo dei macrostati M sono sostanzialmente indipendenti dalla loro definizione precisa, purché le scale macroscopiche e microscopiche siano ampiamente separate.

Consideriamo ora l'evoluzione temporale dei microstati corrispondente a quella dei macrostati M (X); l'evoluzione dei microstati è governata dalla dinamica hamiltoniana che connette un microstato X (t₀) al tempo t₀, al microstato X (t) al tempo t. Chiamiamo X (t₀) e X (t₀ + τ), τ > 0, questi due microstati; invertendo (fisicamente o matematicamente) tutte le velocità al tempo t₀ + τ, otteniamo un nuovo microstato. Se ora seguiamo l'evoluzione durante un nuovo intervallo τ arriviamo a un microstato al tempo t₀ + 2τ che è esattamente lo stato X (t₀) con tutte le velocità invertite. Indicheremo con RX il microstato ottenuto da X invertendo tutte le velocità, RX = (r₁, - v₁, r₂, - v₂, ..., r_N, - v_N).

Ritornando ora alle immagini della fig. 1, è chiaro che esse rimarrebbero immutate se invertissimo le velocità di tutte le particelle; perciò, se X appartiene a Γ_M anche RX appartiene a Γ_M. Appare ora chiaramente quale sia la difficoltà di assegnare un ordinamento temporale definito alle immagini della figura: dire che un macrostato M₁ al tempo t₁ si evolve verso un altro macrostato M₂ al tempo t₂ = t₁ + τ, τ > 0, significa che vi è un microstato X in Γ_M1 che dà origine a un microstato Y a t₂ con Y in Γ_M2. Ma allora RY è anch'esso in Γ_M2 e seguendo l'evoluzione di RY per un tempo τ si otterrebbe lo stato RX che sarebbe allora in Γ_M1. Perciò, dal punto di vista delle leggi della meccanica (che qui supponiamo siano le leggi della natura), la serie di immagini che rappresentano M_A, M_B, M_C e M_D nella fig. 1, in base alle leggi della meccanica classica (che in questo caso assumiamo essere le leggi della natura) potrebbero corrispondere a sequenze temporali che vanno in ambedue le direzioni.

Appare perciò chiaro che la nostra assegnazione dell'ordine temporale alle immagini della fig. 1 non è basata soltanto sulle leggi dinamiche dell'evoluzione, le quali sono compatibili con ambedue gli ordinamenti temporali, ma è piuttosto basata sull'esperienza: una direzione è quella usuale che facilmente s'indovina, mentre l'altra non la si vede mai. Si pone perciò il problema di spiegare la ragione di questo fatto.

3. La risposta di Boltzmann.

Questa domanda fu posta per la prima volta dai fisici teorici, che ne diedero anche la risposta, nella seconda metà del XIX secolo, quando gli esperimenti di Joule e di altri avevano già dimostrato l'applicabilità delle leggi della meccanica ai fenomeni termici. Gli scienziati che maggiormente contribuirono a questo problema furono Maxwell, Thomson e Boltzmann. Una esauriente risposta qualitativa a questo problema venne fornita da Thomson nel bellissimo articolo del 1875 che abbiamo già citato; per quanto ne so, né Boltzmann né altri autori citano mai questo articolo, che avrebbe potuto o dovuto chiarire molte incomprensioni. Tale risposta può venir riassunta con una citazione di Gibbs apparsa sul risvolto di copertina del secondo volume delle lezioni di Boltzmann (v., 1896-1898) sulla teoria cinetica dei gas: ‟in altre parole, l'impossibilità di una diminuzione non compensata di entropia sembra ridursi all'improbabilità" (v. Gibbs, 1876).

Il significato di questa teoria statistica può essere meglio compreso associando a ogni macrostato M, e perciò a ogni punto nello spazio delle fasi che dà origine a M, una ‛entropia di Boltzmann' definita da:

S_B (M) = k log ∣Γ_M∣, (1)

dove k è la costante di Boltzmann e ∣Γ_M∣ è il volume dello spazio delle fasi associato al macrostato M, cioè ∣Γ_M∣ è l'integrale dell'elemento di volume di Liouville invariante nel tempo

esteso a Γ_M (S_B è definita a meno di costanti additive; v. Penrose, 1970).

Il colpo di genio di Boltzmann consistette nel connettere direttamente questa funzione S_B (M (X)), definita microscopicamente, con l'entropia termodinamica di Clausius, S_eq, che è una proprietà estensiva dei sistemi macroscopici in equilibrio definita macroscopicamente e operativamente misurabile (a meno di costanti additive). Per un sistema in equilibrio con una data energia E (definita con un certo margine di errore), un volume V e un numero di particelle N, Boltzmann dimostrò che

S_eq (E, V, N) = Ns_eq (e, n) ≅ S_B(M_eq),

con e = E/N, n = N/V, (2)

dove M_eq (E, V, N) è il macrostato all'equilibrio (corrispondente a M_D nella fig. 1). Con il simbolo ≅ intendiamo che per grandi N, cioè tali che il sistema sia realmente macroscopico, l'uguaglianza valga a meno di termini trascurabili quando si dividano i due membri dell'equazione (2) per N e si sia fissata opportunamente la costante additiva. È importante che le celle usate per definire M_eq contengano molte particelle, cioè che la scala macroscopica sia molto grande rispetto a quella microscopica.

Se si accetta questa identificazione, si può usare l'equazione (1) anche per definire l'entropia (macroscopica) per sistemi non interamente all'equilibrio e identificare così gli aumenti di tale entropia con gli aumenti del volume della regione dello spazio delle fasi Γ_M(X). Questa identificazione spiega in maniera naturale l'osservazione contenuta nella seconda legge della termodinamica, secondo la quale quando si rimuove un vincolo da un sistema macroscopico isolato esso si evolve verso uno stato con entropia maggiore. Più precisamente: supponiamo che inizialmente vi sia una parete che divide i riquadri della fig. 1, e che questa venga rimossa al tempo t_A. Il volume dello spazio delle fasi che il sistema ha a disposizione quando si rimuove la parete è enormemente aumentato: per esempio, se il sistema nella fig. 1 contiene una mole di fluido in un contenitore da un litro, il rapporto fra il volume della regione senza vincoli e quello della regione vincolata è dell'ordine di 2^N, ossia 10¹⁰²⁰, approssimativamente uguale al rapporto ∣Γ_MD∣/∣Γ_MA∣. Possiamo perciò attenderci che, quando si rimuove la parete, il moto del punto X dello spazio delle fasi avverrà con altissima ‛probabilità' verso regioni dello spazio delle fasi divenute in tal modo accessibili, per le quali ∣Γ_M∣ è grande. Ci si può dunque attendere che questo moto continui fino a che X (t) raggiunga Γ_Meq, corrispondente al fatto che il sistema si trova ora nello stato di equilibrio senza vincoli. Dopo tale istante possiamo attenderci di vedere soltanto piccole fluttuazioni attorno all'equilibrio macroscopico, la cui ampiezza è tipicamente dell'ordine della radice quadrata del numero delle particelle interessate. Va sottolineato che un elemento importante di questa analisi è la costanza nel tempo del volume di Liouville degli insiemi nello spazio delle fasi Γ. Senza tale invarianza la connessione tra volume dello spazio delle fasi e probabilità diverrebbe impossibile o almeno molto problematica.

Naturalmente, se il nostro sistema isolato rimane isolato per sempre, in base al teorema della ricorrenza di Poincaré il punto dello spazio delle fasi X (t) dovrebbe ritornare molto vicino al suo valore iniziale X (t_A) e anzi ci ritornerebbe un numero infinito di volte. Tuttavia, i tempi di ricorrenza di Poincaré sono talmente grandi (più o meno dell'ordine del rapporto ∣Γ_MD∣/∣Γ_MA∣) che quando Zermelo avanzò questa obiezione alla spiegazione di Boltzmann della seconda legge, quest'ultimo rispose (v. Boltzmann, 1896-1898): ‟Il teorema di Poincaré, che Zermelo spiega all'inizio del suo articolo, è certamente corretto, ma non la sua applicazione alla teoria del calore. [...] Perciò quando [...] Zermelo, dal fatto teorico che gli stati iniziali in un gas devono essere ricorrenti - senza aver calcolato il tempo necessario perché ciò avvenga - conclude che le ipotesi della teoria dei gas debbano essere scartate o per lo meno cambiate in maniera fondamentale, si comporta come un giocatore di dadi che, avendo calcolato che la probabilità di una sequenza di mille uno non è zero, concludesse che il suo dado deve essere truccato perché non ha ancora osservato una tale sequenza!". Va notato che nello stesso articolo Boltzmann ha scritto anche: ‟Analogamente si osserva che le particelle molto piccole in un gas compiono dei moti che derivano dal fatto che la pressione sulla superficie delle particelle può fluttuare". Ciò mostra che Boltzmann aveva compreso perfettamente la causa del moto browniano dieci anni prima del famoso articolo di Einstein sull'argomento. È sorprendente che egli non abbia mai menzionato questo fenomeno nelle sue discussioni con Ostwald e Mach sulla reale esistenza degli atomi.

Perciò non soltanto le profonde intuizioni di Boltzmann danno un'interpretazione microscopica della misteriosa entropia termodinamica di Clausius, ma esse forniscono anche una generalizzazione naturale dell'entropia agli stati macroscopici di non equilibrio M e perciò una spiegazione della seconda legge della termodinamica, cioè l'espressione formale dell'evoluzione asimmetrica nel tempo degli stati microscopici che si verifica in natura.

4. L'uso della probabilità

Le idee di Boltzmann, come dice Ruelle (v., 1991), sono al tempo stesso semplici e molto acute: esse introducono nelle leggi della natura la nozione di probabilità la quale, almeno a quell'epoca, era del tutto estranea al pensiero scientifico. Infatti, fino ad allora si supponeva che le leggi scientifiche valessero senza alcuna eccezione e non soltanto ‛quasi' sempre: invero non si conoscevano (né si conoscono tuttora) eccezioni alla seconda legge e neppure ci aspettiamo di vederne nel prossimo ‟milione di anni", come dice Feynman (v., 1965) molto prudentemente. La ragione di questo, come avevano compreso Maxwell, Thomson e Boltzmann, sta nel fatto che per un sistema macroscopico la frazione di microstati la cui evoluzione conduce a macrostati con un'entropia S_B maggiore è talmente vicina a uno (in termini del loro volume di Liouville) che tale comportamento è esattamente quello che ci appare debba avvenire ‛sempre'. Per usare le parole di Boltzmann (v., 1896-1898): ‟La legge di Maxwell della distribuzione delle velocità fra le molecole di un gas non è in alcun modo un teorema della meccanica usuale che possa essere dimostrato soltanto a partire dalle equazioni del moto; al contrario, si può soltanto dimostrare che è altamente probabile e che per un gran numero di molecole tutti gli altri stati hanno in confronto una probabilità talmente piccola da poter venir trascurata a tutti i fini pratici". Usando il linguaggio matematico moderno, diremmo che tale comportamento è ‛tipico', intendendo così che l'insieme dei microstati X in Γ_MA in cui si riscontra tale comportamento occupano una frazione di volume che tende a uno al crescere di N. Perciò nella fig. 1 la sequenza che va da A verso D è tipica per un punto dello spazio delle fasi in Γ_MA, mentre quella che va da D verso A ha una ‛probabilità' che tende a zero rispetto a una distribuzione uniforme in Γ_MD quando N tende all'infinito.

Si noti che l'argomento di Boltzmann non richiede effettivamente l'ipotesi che il sistema macroscopico debba trovarsi su lunghi periodi di tempo in regioni diverse Γ_M, cioè in stati macroscopici diversi M per frazioni di tempo esattamente uguali al rapporto fra ∣Γ_M∣ e il volume totale dello spazio delle fasi corrispondente alla sua energia. Tale comportamento, che può essere considerato come una forma debole dell'ipotesi ergodica di Boltzmann - debole perché applicata soltanto a quelle regioni dello spazio delle fasi che rappresentano macrostati Γ_M - sembra del tutto plausibile quando non vi siano costanti del moto che scompongono la superficie dell'energia in regioni con stati macroscopici diversi. Esso appare ancora più plausibile se si tiene conto del fatto che in pratica l'isolamento perfetto non esiste, come vedremo più avanti. Le ‛piccole fluttuazioni' dall'equilibrio che ne conseguono sono certamente compatibili con le osservazioni. (Anche la forma forte dell'ipotesi ergodica sembra essere un'ipotesi naturale per sistemi macroscopici e permette di derivare in maniera semplice molte delle loro proprietà di equilibrio).

5. Condizioni iniziali

Una volta accettata la spiegazione statistica del perché un sistema macroscopico evolva in maniera tale che S_B cresca col tempo, resta ancora lo spinoso problema (del quale Boltzmann era ben consapevole) di che cosa si intenda con l'espressione ‛col tempo'. Poiché le leggi della dinamica microscopica sono simmetriche, le due direzioni della variabile temporale sono a priori equivalenti e tali devono rimanere anche a posteriori (v. Schrödinger, 1944). In particolare, se un sistema con un profilo di densità macroscopico non uniforme, ad esempio M_B al tempo t_B nella fig. 1, avesse un microstato che è tipico per Γ_MB, allora quasi sicuramente il suo macrostato sarebbe del tipo di M_C sia al tempo t_B + τ che al tempo t_B - τ. Ciò è inevitabile: poiché la regione nello spazio delle fasi Γ_MB, corrispondente a M_B a un dato tempo t_B, è invariante sotto la trasformazione X → RX, si deve prevedere lo stesso sia per t_B - τ che per t_B + τ. Tuttavia, l'esperienza dimostra che l'ipotesi di tipicità al tempo t_B conduce al comportamento corretto soltanto per tempi t > t_B e non per tempi t 〈 t_B. In particolare, dati soltanto M_B e M_C, non abbiamo alcuna esitazione a situare M_B prima di M_C.

Se ragioniamo più a fondo su come stabiliamo l'ordine di M_B e M_C, ci accorgiamo che esso sembra derivare dalla nostra ipotesi che M_B sia esso stesso così improbabile che deve essersi evoluto da uno stato iniziale di entropia ancora minore, come M_A. Da un microstato iniziale tipico del macrostato M_A, che può facilmente essere creato sperimentalmente, otteniamo il comportamento monotono di S_B con l'ordinamento temporale M_A, M_B, M_C e M_D. Se invece il sistema nella fig. 1 fosse stato completamente isolato per un tempo molto lungo rispetto al suo tempo di rilassamento idrodinamico, allora ci aspetteremmo di trovarlo sempre nel suo stato di equilibrio M_D (eventualmente con alcune piccole fluttuazioni intorno a esso). Messi di fronte alle quattro figure, in questo caso (estremamente improbabile) non avremmo invece alcuna base per assegnare loro un ordine; la reversibilità microscopica ci assicura che le fluttuazioni attorno all'equilibrio sono tipicamente simmetriche negli intorni degli istanti in cui vi è un minimo locale di S_B. In assenza di qualsiasi conoscenza sulla storia del sistema prima e dopo la sequenza di immagini della fig. 1, usiamo la nostra esperienza per concludere che lo stato di bassa entropia M_A doveva essere uno stato iniziale preparato. Come dice Roger Penrose (v., 1989): ‟La asimmetria temporale deriva soltanto dal fatto che il sistema è ‛partito' in uno stato molto particolare (cioè di bassa entropia) e, avendo fatto partire il sistema da questo stato, abbiamo osservato la sua evoluzione nella direzione futura".

La questione è che un microstato corrispondente a M_B (al tempo t_B) che deriva da M_A (al tempo t_A) deve essere in qualche modo ‛atipico' per i punti in Γ_MB. Ciò avviene perché, in virtù del teorema di Liouville, l'insieme Γ_AB di tutti questi punti nello spazio delle fasi ha un volume ∣Γ_AB∣ ≤ ∣Γ_MA∣ che è di gran lunga minore di ∣Γ_MB∣. Tuttavia ciò non impedisce alla stragrande maggioranza dei punti in Γ_AB (rispetto alla misura di Liouville su Γ_AB che è la stessa della misura di Liouville su Γ_A) di avere macrostati futuri come quelli tipici di Γ_B, nonostante che questi ultimi siano molto particolari e non rappresentativi di Γ_MB per quanto riguarda i loro macrostati passati. Questo comportamento è stato esplicitamente dimostrato da Lanford (v., 1981) nella sua deduzione dell'equazione di Boltzmann ed è implicito in tutte le deduzioni delle equazioni idrodinamiche (v. Lebowitz e Spohn, 1983; v. Lebowitz e altri, 1988; v. De Masi e Presutti, 1991; v. Spohn, 1991). Per rendersi conto intuitivamente dell'origine di tale comportamento osserviamo che, per sistemi con interazioni realistiche, il dominio Γ_AB risulterà così convoluto da essere ‛essenzialmente denso' in Γ_B, sicché ogni suo minimo ispessimento copre tutto Γ_MB. Non è perciò irragionevole attendersi che il loro comportamento futuro, per quanto riguarda i macrostati, risulterà sostanzialmente inalterato dalla loro storia passata.

Ciò può essere dimostrato completamente per un modello di sistema macroscopico in cui ognuno degli N (N molto grande) atomi non interagenti sia specificato non da (r, v) ma da σ = (..., σ_-2, σ_-1; σ₀, σ₁, ...), cioè da una sequenza bilatera infinita di 0 e 1 (in modo equivalente a un punto in un quadrato unitario). La loro dinamica con tempo discreto è quella di una traslazione a sinistra (Tσ)_i = σ_i+1 (detta talvolta la ‛trasformazione del fornaio'). Se definiamo ‛l'inversione delle velocità' con (Rσ)_i = σ_-i-1 e il macrostato M (σ) con k valori M (σ) = (σ₀ + σ_-1, σ₁ + σ_-2, σ₂ + σ_-3, ..., σ_k-1 + σ_-k) si può facilmente dimostrare che il comportamento futuro dei punti tipici in Γ_MAB è in effetti quello descritto più sopra.

6. Origine degli stati a bassa entropia

Non vi è alcuna difficoltà a creare in laboratorio stati iniziali di bassa entropia come quello rappresentato nella fig. 1. I sistemi di laboratorio sono preparati in stati di bassa entropia di Boltzmann da scienziati i quali sono essi stessi in stati di bassa entropia. Come tutti gli altri esseri viventi, gli scienziati sono nati in tali stati e la loro entropia resta bassa poiché si cibano di alimenti a bassa entropia, i quali a loro volta sono prodotti da piante che utilizzano la radiazione a bassa entropia proveniente dal Sole. Tutto ciò era già ben chiaro a Boltzmann, come risulta dal seguente brano: ‟La lotta per l'esistenza degli esseri viventi non è perciò una lotta per procurarsi gli elementi - gli elementi di tutti gli organismi sono disponibili in abbondanza nell'aria, nell'acqua e nel suolo - e neppure per l'energia, che è abbondante sotto la forma di calore, sfortunatamente non trasformabile, in ogni corpo. È piuttosto una lotta per l'entropia che diviene disponibile attraverso il flusso di energia dal Sole caldo alla Terra fredda. Per utilizzare al massimo questa energia, le piante dispiegano immense aree di foglie e catturano l'energia del Sole con un processo ancora inesplorato, prima che essa scenda al livello di temperatura della nostra Terra, per effettuare le sintesi chimiche ancora sconosciute nei nostri laboratori. Sono i prodotti di questa cucina chimica gli oggetti della lotta nel mondo animale" (cit. in Broda, 1955).

Si osservi che mentre questi scienziati si sono evoluti, grazie a questa sorgente di energia a bassa entropia, in esseri capaci di preparare particolari sistemi macroscopici con valori bassi di S_B(M), come il nostro stato M_A, l'entropia totale S_B, compresa l'energia degli scienziati e quella del loro ambiente, è destinata a crescere continuamente: non esistono diavoli di Maxwell. La bassa entropia del sistema solare si manifesta anche in eventi nei quali non vi è alcuna partecipazione umana: così, per esempio, se invece della fig. 1 ci fossero mostrate delle immagini della cometa Shoemaker-Levy e di Giove prima e dopo la loro collisione, la direzione del tempo sarebbe anche in questo caso del tutto ovvia.

Dobbiamo allora domandarci qual è l'origine di questo stato di bassa entropia del sistema solare. Per rispondere a questa domanda siamo portati più o meno inevitabilmente a considerare uno stato dell'universo iniziale dotato di un'entropia di Boltzmann molto bassa. Citiamo ancora Boltzmann: ‟Che in natura la transizione da uno stato probabile a uno improbabile non avvenga tanto sovente quanto la transizione inversa, può essere spiegato ammettendo uno stato iniziale molto improbabile dell'intero universo che ci circonda. È questa un'ipotesi ragionevole, poiché ci permette di spiegare i fatti dell'esperienza e non c'è da attendersi di riuscire a dedurla da niente di più fondamentale" (cit. in Broda, 1955). Dobbiamo cioè supporre che l'universo sia stato ‛creato' in un microstato X tipico di qualche macrostato M₀ per il quale ∣Γ_M0∣ sia una frazione molto piccola del volume dello spazio delle fasi disponibile. All'epoca di Boltzmann non esisteva alcuna teoria fisica per immaginare un tale stato iniziale e Boltzmann accarezzò l'idea che potesse trattarsi di una fluttuazione ampia ed estremamente improbabile in un universo eterno che per la maggior parte del tempo si trova in uno stato di equilibrio. Feynman (v., 1965) ha dimostrato in maniera convincente l'improbabilità di un tale punto di vista.

Nell'attuale scenario del big bang è plausibile, come argomenta Penrose (v., 1989), prendere come stato iniziale lo stato dell'universo subito dopo il big bang. Il suo macrostato sarebbe allora quello in cui la densità di energia è approssimativamente uniforme nello spazio. Penrose valuta che se M_f è il macrostato della grande implosione finale (big crunch), con un volume nello spazio delle fasi ∣Γ_mf∣, il valore del rapporto fra i due volumi, finale e iniziale, sarebbe ∣Γ_Mf∣/∣Γ_M0∣ ≈ 10¹⁰¹²³. L'enorme valore di ∣Γ_Mf∣ in confronto a ∣Γ_M0∣ è la conseguenza dell'enorme spazio delle fasi che corrisponde a un universo collassato entro un buco nero (v. fig. 2).

Non so se questi stati iniziali e finali siano plausibili, ma in ogni caso bisogna concordare con Feynman (v., 1965) quando dice che ‟è necessario aggiungere alle leggi fisiche l'ipotesi che in passato l'universo sia stato più ordinato, in senso tecnico, di quanto lo sia oggi [...] se si vuol rendere comprensibile l'irreversibilità". Il ‟senso tecnico" si riferisce chiaramente al fatto che lo stato iniziale dell'universo M₀ aveva un'entropia S_B minore di quella dello stato attuale. Se si accetta l'esistenza di un tale macrostato M₀, si può supporre che il microstato iniziale fosse tipico per Γ_M0. Si può allora applicare la statistica per calcolare l'evoluzione tipica di un tale stato iniziale, vale a dire si possono usare argomenti basati sul volume dello spazio delle fasi per predire il comportamento futuro dei sistemi macroscopici, non però per determinare il passato. Come disse Boltzmann, ‟se siamo disposti ad accettare il punto di vista statistico non occorre ipotizzare un tipo speciale di condizione iniziale per dare una prova meccanica della seconda legge [...] se lo stato iniziale è scelto a caso [...] l'entropia quasi sicuramente crescerà" (cit. in Brush, 1966).

7. Irreversibilità e stabilità macroscopica

Naturalmente la meccanica non impedisce l'esistenza di un microstato X per il quale S_B (M (X_t)) decresce al crescere di t. Uno sperimentatore potrebbe, in linea di principio, invertire tutte le velocità del sistema nella fig. 1B e osservare poi il sistema che si separa. Sembra tuttavia impossibile farlo in pratica: anche se si riuscisse a invertire perfettamente le velocità, come avviene in maniera imperfetta negli esperimenti di eco di spin (v. Hahn, 1950; v. Zhang e altri, 1992), non dovremmo attenderci di vedere il sistema della fig. 1 passare da M_B a M_A, cosa per la quale sarebbe necessario che sia l'inversione delle velocità sia l'isolamento del sistema fossero assolutamente perfetti. La ragione per la quale una tale perfezione è necessaria in questa situazione e non nella precedente sta nel fatto che il comportamento macroscopico di un sistema con un microstato Y nello stato M_B che proviene da un microstato X tipico per Γ_MA è stabile rispetto alle perturbazioni per quanto riguarda il suo futuro, mentre è molto instabile per quanto riguarda il suo passato (e perciò rispetto al futuro di RY) (v. figg. 3 e 4).

Abbiamo considerato essenzialmente situazioni del tipo di quelle rappresentate nella fig. 1, dove l'evoluzione macroscopica è descritta dall'equazione di diffusione stabile; però, anche in situazioni diverse - come quella della turbolenza, nella quale l'evoluzione macroscopica in avanti è caotica, cioè sensibile a piccole perturbazioni - l'evoluzione in avanti avviene con aumento di entropia. Tuttavia, per l'evoluzione isolata di un microstato con velocità invertite si ottiene una diminuzione di S_B, mentre nel caso di evoluzioni perturbate si può prevedere di avere, almeno dopo un periodo di tempo assai breve, un aumento di S_B. Perciò, anche in regimi macroscopicamente ‛caotici', l'evoluzione in avanti di M è in questo senso molto più stabile di quella in direzione opposta. Così in regime turbolento le evoluzioni in avanti sono ancora descritte da soluzioni della stessa equazione di Navier-Stokes, mentre l'evoluzione macroscopica in senso inverso di un fluido perfettamente isolato e quella di un fluido reale non hanno alcuna relazione fra loro.

L'analisi precedente è basata sull'ipotesi del tutto ragionevole che quasi ogni perturbazione del microstato Y tenda a renderlo più tipico del suo macrostato M (Y), che in questo caso è uguale a M_B; la perturbazione perciò non interferisce con il comportamento tipico di Γ_MB. D'altra parte, l'evoluzione in avanti dello stato imperturbato RY è, per costruzione, diretta verso volumi più piccoli dello spazio delle fasi ed è perciò atipica per Γ_MB. Ciò significa che si richiede in questo caso una ‛mira perfetta' e perciò più facilmente deviata da perturbazioni anche assai piccole nell'inversione e/o da minime influenze esterne. Dopo un tempo molto breve, durante il quale S_B decresce, le imperfezioni nell'inversione e le perturbazioni esterne come quelle che provengono da un'esplosione solare, un terremoto stellare in una galassia distante (avvenuta molto tempo fa) o dal battere delle ali di una farfalla (v. Ruelle, 1991), la faranno crescere di nuovo. Ciò è in un certo senso simile a un flipper, in cui il giocatore deve mandare una biglia in una zona particolarmente piccola: per riuscire a mandarvi la biglia bisogna agire con grande precisione, ma basta pochissimo perché vada in zone più ampie. Per i sistemi macroscopici che stiamo considerando, la differenza fra le dimensioni relative delle regioni analoghe nello spazio delle fasi è incredibilmente più grande. A meno che vi sia una ‛grande cospirazione', è possibile prevedere con sicurezza che il comportamento sarà in accordo con la seconda legge (a parte forse per tempi molto brevi).

La sensibilità alle piccole perturbazioni per la direzione in cui l'entropia decresce si osserva comunemente nelle simulazioni al calcolatore di sistemi con interazioni ‛realistiche', dove si può ottenere facilmente l'inversione della velocità e dove gli inevitabili errori di arrotondamento giocano il ruolo delle perturbazioni. Tuttavia, nelle simulazioni è possibile evitare questo effetto usando un'aritmetica intera in tempi discreti, come mostrano chiaramente le figg. 3 e 4; quest'ultima mostra anche come una piccola perturbazione che non ha alcun effetto nella macroevoluzione in avanti distrugga completamente l'evoluzione temporale in senso inverso. Questo punto è stato già chiaramente formulato da Thomson (v., 1875): ‟La dissipazione dell'energia, come quella dovuta per esempio alla conduzione del calore in un gas, può essere completamente impedita con un'opportuna disposizione di diavoli di Maxwell che agiscono conformemente alle leggi della conservazione dell'energia e dell'impulso. Se invece non vi sono diavoli, il risultato medio dei moti liberi delle molecole tende a equalizzare le differenze di temperatura. Se permettiamo a questo processo di procedere per un certo tempo e poi invertiamo i moti di tutte le molecole, osserveremo una disequalizzazione. Tuttavia, se il numero delle molecole è molto grande, come avviene in un gas, ogni più piccola deviazione dalla precisione assoluta nell'inversione delle velocità accorcerà enormemente il tempo durante il quale tale disequalizzazione ha luogo. In altre parole, la probabilità che si produca una distribuzione delle velocità che conduca a differenze di temperatura per un tempo percepibile è molto piccola. Inoltre, se si tiene conto del fatto che nessun sistema fisico può essere completamente isolato dall'ambiente circostante, mentre invece in linea di principio interagisce con tutte le altre molecole dell'universo, e se crediamo che il numero di tali molecole sia infinito, dobbiamo allora concludere che è impossibile che si producano spontaneamente differenze di temperatura. Un calcolo numerico illustra questa conclusione". Thomson continua dicendo: ‟L'essenza della scoperta di Joule è stata quella di stabilire che tutti i fenomeni fisici sono soggetti alle leggi dinamiche. Pertanto, se il moto di ogni particella di materia nell'universo fosse esattamente invertito a un dato istante, il corso della natura sarebbe semplicemente invertito da allora in poi. Le bollicine di schiuma ai piedi di una cascata si riunirebbero rientrando nell'acqua; [...] i detriti riprenderebbero dal fango i materiali occorrenti per ricostruirsi nelle proprie irregolari forme precedenti e si riunirebbero sulla sommità della montagna dalla quale si erano staccati. E se l'ipotesi materialistica della vita fosse vera, anche le creature viventi crescerebbero all'inverso, conoscendo il futuro ma senza ricordo del passato, e diverrebbero di nuovo non nati. Ma i fenomeni reali della vita trascendono la scienza umana, talché queste speculazioni concernenti le conseguenze di questa supposta inversione sono del tutto sterili. Ben diversa è invece la situazione per quanto riguarda l'inversione dei moti della materia inanimata e anche queste considerazioni elementari sono sufficienti a spiegare completamente la teoria della dissipazione dell'energia".

8. Confronto fra le entropie di Boltzmann e di Gibbs

Il punto di vista boltzmanniano, che si concentra sull'evoluzione di un sistema macroscopico particolare, è concettualmente diverso da quello gibbsiano che prende in considerazione gli insiemi statistici. Questa differenza si manifesta in modo evidente quando si paragona l'entropia di Boltzmann - definita nella (1) per un microstato X di un sistema macroscopico - con l'entropia S_G di Gibbs, più comunemente usata, definita per una densità di insieme ρ (X) dalla relazione:

dove ρ (X) dX è la probabilità che lo stato microscopico del sistema si trovi nel volume dello spazio delle fasi dX e dove l'integrale è esteso a tutto lo spazio delle fasi Γ. Se ρ (X) è l'insieme microcanonico generalizzato associato al macrostato M, cioè:

allora si ha naturalmente

S_G (_ρM) = k log ∣Γ_M∣ = S_B (M). (5)

Gli insiemi microcanonici generalizzati del tipo di ρ_M (X), o la loro versione canonica, sono comunemente impiegati per descrivere sistemi in cui la densità delle particelle, la densità di energia e la densità di quantità di moto variano lentamente su scala microscopica e il sistema è, in ciascuna piccola regione macroscopica, in equilibrio alle densità locali prescritte, cioè quando si ha equilibrio locale (v. Lebowitz e altri, 1988; v. De Masi e Presutti, 1991; v. Spohn, 1991). In questi casi S_G (_ρM) e S_B (M) coincidono fra di loro e con l'entropia idrodinamica macroscopica.

Si noti tuttavia che, a meno che il sistema sia in equilibrio completo e che non vi siano ulteriori cambiamenti sistematici in M o ρ, l'evoluzione temporale di S_G e S_B è molto diversa. Com'è ben noto, dal fatto che il volume delle regioni dello spazio delle fasi rimane invariato nell'evoluzione temporale hamiltoniana (ancorché le loro forme cambino grandemente) segue che S_G (_ρ) non cambia nel tempo fintantoché l'evoluzione di X è hamiltoniana, cioè se ρ si evolve secondo l'equazione di Liouville; S_B (M), invece, cambia grandemente. Perciò se consideriamo l'evoluzione dell'insieme microcanonico corrispondente al macrostato M_A nella fig. 1A dopo che si è rimosso il vincolo, S_G sarà inizialmente uguale a S_B, ma successivamente S_B crescerà mentre S_G resterà costante. Pertanto, S_G non può dare alcuna indicazione che il sistema stia evolvendo verso l'equilibrio.

Ciò riflette il fatto, discusso più sopra, che il microstato X (t) non rimane tipico per lo stato di equilibrio locale M (t) per t > 0. Fino a che il sistema rimane assolutamente isolato, lo stato T_tX contiene deboli correlazioni che si riflettono nella forma complicata che una regione iniziale Γ_M assume al variare del tempo, ma che non hanno effetto sull'evoluzione temporale di M (v. cap. 5). Perciò l'entropia rilevante per spiegare l'evoluzione temporale di un sistema macroscopico è S_B e non S_G. Naturalmente, se effettuiamo una media a ‛grana grossa' (coarse grained) di ρ sulle celle Γ_M ritorniamo a utilizzare ρ_M, o una sovrapposizione di ρ_M, e ci ritroviamo a definire S_B a ritroso.

9. Osservazioni

La caratterizzazione di un macrostato M, fatta generalmente attraverso campi di densità nello spazio tridimensionale come nella fig. 1, può estendersi a descrizioni mesoscopiche. Ciò è particolarmente utile per un gas rarefatto, dove M può venire utilmente caratterizzato dalla densità nello spazio a sei dimensioni delle posizioni e velocità della singola molecola. L'evoluzione macroscopica, o mesoscopica, di questo M è allora data dalla equazione di Boltzmann e S_B (M) coincide con la famosa funzione H di Boltzmann cambiata di segno.

Va tuttavia sottolineato che per i sistemi nei quali l'energia potenziale è importante, come per esempio nei gas densi, la funzione H non coincide con S_B; inoltre, - H (ma non S_B) decresce per opportune condizioni macroscopiche iniziali. Com'è stato osservato da Jaynes (v., 1971), questo accade ogni volta che si parte da un'energia totale E e da un'energia cinetica K = K₀ tale che K₀ > K_eq (E), in cui K_eq (E) è il valore che K assume quando il sistema è in equilibrio con energia E. Questo si vede facilmente se il macrostato iniziale è tale che la densità spaziale è uniforme e la distribuzione è maxwelliana con una temperatura appropriata T₀ = ²3−%%K₀/kN. Quando il sistema va all'equilibrio la temperatura diminuisce e - H, che per una distribuzione maxwelliana è proporzionale a log T, sarà perciò più piccola nello stato di equilibrio quando T = T_eq (E) > T₀.

La formula di Einstein per la probabilità delle fluttuazioni in un sistema di equilibrio,

probabilità di M ~ exp [S (M) - S_eq]/k, (6)

è essenzialmente l'inversione delle formule (4) e (5). Combinando questa relazione con l'osservazione che l'entropia S_B (M) di un sistema macroscopico preparato in un dato stato non uniforme M può essere calcolata con considerazioni termodinamiche macroscopiche, si ottengono dei risultati interessanti. In particolare, se si sviluppa S_B (M) nell'esponenziale intorno a M_eq e si prendono solo i termini quadratici, si ottiene una distribuzione gaussiana per le normali (piccole) fluttuazioni attorno all'equilibrio. È questa una delle considerazioni essenziali su cui si basano le relazioni di reciprocità di Onsager (v., 1931).

10. Conclusioni

Il comportamento asimmetrico rispetto al tempo osservato in generale nei sistemi macroscopici - espresso dalla seconda legge della termodinamica - ha origine nelle leggi microscopiche simmetriche rispetto al tempo a causa della grande disparità tra scala microscopica e scala macroscopica. Caratteristiche più specifiche dell'evoluzione macroscopica dipendono dalla natura della dinamica microscopica. In particolare, le interazioni a corto raggio con buone proprietà di mescolamento conducono, nel caso di sistemi semplici, a descrizioni quantitative di tali evoluzioni per mezzo delle equazioni idrodinamiche autonome, per esempio l'equazione di diffusione.

Queste equazioni deterministiche asimmetriche rispetto al tempo descrivono accuratamente il comportamento dei macrosistemi ‛individuali'. Le derivazioni teoriche di queste equazioni che usano insiemi statistici (o distribuzioni di probabilità) per essere efficaci devono quindi essere valide per quasi tutti i membri dell'insieme, cioè presentarsi con probabilità prossima a 1. Identificare il comportamento macroscopico irreversibile con l'evoluzione temporale degli insiemi che descrivono sistemi aventi solo pochi gradi di libertà, dove la caratteristica di tipicità non è valida, è fuorviante e ingannevole.

Infine, va notato che nella discussione precedente abbiamo trattato esclusivamente di quello che normalmente si chiama la ‛freccia termodinamica del tempo' e della sua relazione con lo stato cosmologico iniziale. Sono state escluse altre frecce del tempo, quali l'asimmetria fra potenziali elettromagnetici avanzati e ritardati o la ‛causalità': a nostro parere queste sono tutte manifestazioni dello stato iniziale a bassa entropia dell'universo, e riteniamo pure che la violazione dell'invarianza per inversione del tempo nelle interazioni deboli non sia rilevante per la discussione della irreversibilità macroscopica.

BIBLIOGRAFIA

Aharonov, J., Bergmann, P. G., Lebowitz, J. L., Time symmetry in the quantum process of measurement, in ‟Physical review", 1964, CXXXIV, pp. 1410-1416.

Bell, J. S., Speakable and unspeakable in quantum mechanics, New York 1987.

Boltzmann, L., Entgegnung auf die wärme- theoretischen Betrachtungen des Hrn. E. Zermelo, in ‟Annalen der Physik und Chemie", 1896, LVII, pp. 772-784.

Boltzmann, L., Vorlesungen über Gastheorie, 2 voll., Leipzig 1896-1898 (tr. ingl.: Lectures on gas theory, London 1964).

Broda, E., Ludwig Boltzmann. Mensch, Physiker und Philosoph, Berlin 1955 (tr. ingl.: Ludwig Boltzmann, man-physicist-philosopher, Woodbridge, Conn., 1983).

Brush, S. G., Kinetic theory, Oxford 1966.

Brush, S. G., The kind of motion we call heat: a history of the kinetic theory of gases in the 19th century, Amsterdam 1976.

Cohen, E. G. D., Thirring, W. (a cura di), The Boltzmann equation: theory and applications, Vienna 1973.

De Masi, A., Presutti, E., Mathematical methods for hydrodynamic limits, New York 1991.

Dürr, D., Goldstein, S., Zanghi, N., Quantum equilibrium and the origin of absolute uncertainty, in ‟Journal of statistical physics", 1992, LXVII, pp. 843-907.

Feynman, R. P., The character of physical law, Cambridge 1965 (tr. it.: La legge fisica, Torino 1971).

Feynman, R. P., Leighton, R. B., Sands, M., The Feynman lectures on physics, 3 voll., Reading, Mass., 1963-1965 (tr. it.: La fisica di Feynman, 3 voll., Milano 1985).

Gallavotti, G., Ergodicity, ensembles, irreversibility in Boltzmann and beyond, The Erwin Schrödinger International Institute for Mathematical Physics (ESI) preprint n. 81, Vienna 1994.

Gibbs, J. W., On the equilibrium of heterogeneous substances, in ‟Connecticut Academy transactions", 1876, III, pp. 108-248 (ora in: The scientific papers of Willard Gibbs, New York 1961, vol. I, pp. 55-195).

Hahn, E. L., Spin echoes, in ‟Physical review", 1950, LXXX, pp. 580-594.

Halliwell, J. J., Pérez-Mercader, J., Zurek, W. H. (a cura di), Physical origins of time asymmetry, Cambridge 1994.

Jaynes, E. T., Violation of Boltzmann's H theorem in real gases, in ‟Physical review. A", 1971, IV, pp. 747-750.

Lanford, O., The hard sphere gas in the Boltzmann-Grad limit, in ‟Physica A", 1981, CVI, pp. 70-76.

Lebowitz, J. L., Macroscopic laws, microscopic dynamics, time's arrow and Boltzmann entropy, in ‟Physica A", 1993, CXCIV, pp. 1-27.

Lebowitz, J. L., Presutti, E., Spohn, H., Macroscopic models of hydrodynamic behavior, in ‟Journal of statistical physics", 1988, LI, pp. 841-862.

Lebowitz, J. L., Spohn, H., On the time evolution of macroscopic systems, in ‟Communications on pure and applied mathematics", 1983, XXXVI, pp. 595-613.

Levesque, D., Verlet, L., Molecular dynamics and time reversibility, in ‟Journal of statistical physics", 1993, LXXII, pp. 519-537.

Maxwell, J. C., Theory of heat, New York 1872, Westport, Conn., 1970³.

Muntz, E. P., Weaver, D. P., Campbell, D. H. (a cura di), Rarefied gas dynamics: theoretical and computational techniques, Washington 1989.

Nadiga, B. T., Broadwell, J. E., Sturtevant, B., Study of a multispeed cellular automaton, in Rarefied gas dynamics: theoretical and computational techniques (a cura di E. P. Muntz, D. P. Weaver e D. H. Campbell), Washington 1989, pp. 155-170.

Onsager, L., Reciprocal relations in irreversible processes, in ‟Physical review", 1931, XXXVII, pp. 405-426 e XXXVIII, pp. 2265-2279.

Page, D. N., No time asymmetry from quantum mechanics, in ‟Physical review letters", 1993, LXX, pp. 4034-4037.

Penrose, O., Foundations of statistical mechanics, Elmsford, N. Y., 1970.

Penrose, R., The Emperor's new mind, Oxford-New York 1989 (tr. it.: La mente nuova dell'imperatore, Milano 1992).

Ruelle, D., Hasard et chaos, Paris 1991 (tr. it.: Caos e caso, Torino 1992).

Schrödinger, E., What is life?, London 1944 (tr. it.: Che cos'è la vita?, Milano 1944).

Spohn, H., Large scale dynamics of interacting particles, New York 1991.

Thomson, W., The kinetic theory of the dissipation of energy, in ‟Proceedings of the Royal Society of Edinburgh", 1875, VIII, pp. 325-345.

Zhang, S., Maier, B. H., Ernst, R. R., Polarization echoes in NMR, in ‟Physical review letters", 1992, LXIX, pp. 2149-2151.