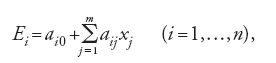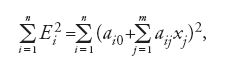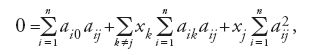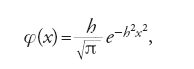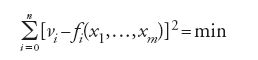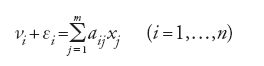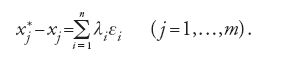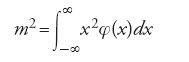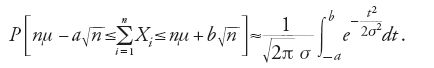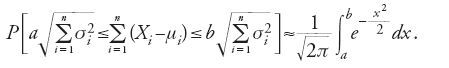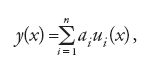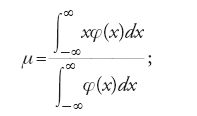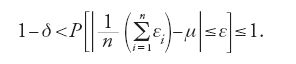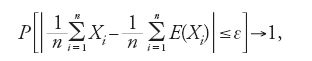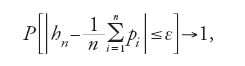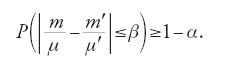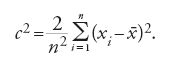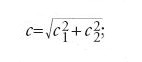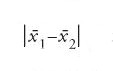L'Ottocento: matematica. Calcolo delle probabilità e statistica
Storia della Scienza (2003)
L'Ottocento: matematica. Calcolo delle probabilita e statistica
Calcolo delle probabilità e statistica
Il ruolo di Laplace nella stocastica del XIX secolo
Numerosi autori hanno contribuito in vario modo allo sviluppo del calcolo delle probabilità e della statistica del XIX sec.; nei loro scritti un nome spicca tra tutti gli altri per la frequenza con cui viene menzionato e indicato come modello: quello di Pierre-Simon de Laplace (1749-1827).
Sebbene il ruolo di Laplace per gli sviluppi del calcolo delle probabilità e in parte anche della statistica dell'Ottocento sia messo in evidenza quasi sempre quando si parla della storia di questa branca della matematica, raramente viene spiegato perché e per quanto tempo i suoi contributi hanno avuto un'importanza tanto decisiva.
L'influenza di Laplace sul calcolo delle probabilità si è protratta perlomeno sino agli anni Settanta dell'Ottocento, come dimostra per esempio il Traité du calcul des probabilités, apparso nel 1873, di Matthieu-Paul-Hermann Laurent (1841-1908), répétiteur d'analyse e successivamente examinateur all'École Polytechnique. L'opera di Laurent pone fine a una lunga stasi nella trattatistica francese sul calcolo delle probabilità e precede i famosi contributi di Joseph-Louis-François Bertrand (1822-1900) e di Jules-Henri Poincaré (1854-1912), i quali peraltro manifestano già una certa emancipazione dal modello sino allora dominante di Laplace. Con il Traité, Laurent si proponeva di fornire le basi matematiche che rendessero accessibile al lettore medio la Théorie analytique des probabilités di Laplace, considerata all'epoca estremamente ardua. Lavori precedenti come il trattato di Sylvestre-François Lacroix (1765-1843), risalente al 1816, o quello di Antoine-Augustin Cournot (1801-1877), pubblicato nel 1843, per il loro carattere elementare si dimostravano infatti del tutto inadeguati allo scopo. Le Recherches di Siméon-Denis Poisson (1781-1840), pubblicate nel 1837, apparivano a Laurent sufficientemente sofisticate sul piano analitico per costituire un'introduzione all'opera di Laplace, e tuttavia a suo giudizio non ne esaurivano i contenuti. Egli attribuiva un'importanza particolare all'opera di Laplace in quanto, a suo avviso, era l'unica dedicata al calcolo delle probabilità che abbracciasse l'intera 'scienza del caso'. Per questa ragione egli volle offrire a tutti coloro che erano interessati alla materia e, soprattutto, agli ufficiali di artiglieria e ai funzionari delle assicurazioni, un'introduzione elementare ma adeguata allo studio dell'intera letteratura disponibile. A differenza di Laplace, Laurent non si occupò del concetto di speranza o aspettativa morale, impostosi all'attenzione con il paradosso di Pietroburgo, né dell'applicazione del calcolo delle probabilità alle decisioni giudiziarie e alle testimonianze, a causa del loro carattere paradossale o non scientifico. Escludendo queste applicazioni, oltre ai necessari metodi analitici, i cardini del calcolo delle probabilità secondo Laurent erano i seguenti: (1) la legge dei grandi numeri e il teorema del limite centrale; (2) la teoria degli errori, in particolare il metodo dei minimi quadrati; (3) le assicurazioni.
La bibliografia straordinariamente ricca che chiude il Traité di Laurent dimostra che all'epoca il calcolo delle probabilità, fatta eccezione per le applicazioni nel campo assicurativo, si era ridotto alla teoria degli errori e alle leggi dei grandi numeri. Essa mette in luce altresì il vuoto di trent'anni che intercorre fra il trattato di Cournot del 1843 e quello di Laurent. In una conferenza tenuta nel 1903 il matematico belga Paul Mansion (1844-1919) imputò tale interruzione allo scarso spazio dato al calcolo delle probabilità nel sistema di istruzione francese. Sino al 1900 la materia era trattata soltanto in maniera occasionale come appendice al corso di fisica matematica alla Sorbona e all'École Polytechnique le veniva dedicato un certo numero di lezioni nei corsi di analisi e di astronomia.
Lo stesso discorso vale per la Germania che nella seconda metà dell'Ottocento andava acquistando una posizione di spicco nel campo della matematica. La maggior parte dei docenti di matematica nelle varie università tedesche trattava soltanto occasionalmente il calcolo delle probabilità, ricalcando più o meno fedelmente le orme di Laplace. Diverso è il discorso che riguarda la teoria degli errori, la quale divenne presto oggetto di corsi di insegnamento regolari a seguito dell'influenza esercitata da Carl Friedrich Gauss (1777-1855) e dalla sua scuola sullo sviluppo dell'astronomia e della geodesia.
Il paese europeo in cui il calcolo delle probabilità si affermò prima e più compiutamente fu però, a parte la Russia, il Belgio. Un ruolo determinante a questo riguardo va riconosciuto senz'altro a Lambert-Adolphe-Jacques Quételet (1796-1874), fondatore di una statistica intesa come fisica sociale che aveva suscitato uno straordinario interesse ben al di là dei confini del Belgio. Dal 1835 in questo paese il calcolo delle probabilità costituiva una materia fondamentale del corso di laurea in fisica e matematica e nel 1836 era entrato a far parte del programma di studi dei politecnici. Non sorprende pertanto che in Belgio, accanto a vari scritti di Quételet e alle sue Lettres à S.A.R. le duc régnant de Saxe-Cobourg et Gotha sur la théorie des probabilités, appliquée aux sciences morales et politiques del 1846, concepite per il grande pubblico, fossero pubblicati nel 1852 un manuale sulla teoria della probabilità con particolare riguardo alla teoria degli errori, di Jean-Baptiste-Joseph Liagre (1815-1891) e una monografia sul metodo dei minimi quadrati di Pierre-Ernest Biver, cui seguirono nel 1874 le lezioni sul calcolo delle probabilità tenute da Antoine Meyer (1803-1875) all'Università di Liegi, pubblicate in traduzione tedesca già nel 1879. Al pari di Laurent diversi matematici belgi, come lo stesso Meyer ed Emmanuel-Joseph Boudin (1820-1893), che insegnò per quasi mezzo secolo, sino al 1892, presso l'Università di Gand e l'école du Génie, concepivano l'insegnamento del calcolo delle probabilità unicamente come introduzione alla Théorie analytique des probabilités di Laplace.
Risalgono all'ultimo ventennio dell'Ottocento i primi accenni di un nuovo sviluppo, peraltro destinato ad affermarsi pienamente soltanto nel XX sec., che avrebbe portato a una rottura con il modello 'classico' della probabilità codificato da Laplace. Questa svolta si intravede già nella celebre conferenza tenuta da David Hilbert (1862-1943) al Secondo congresso internazionale dei matematici a Parigi. Nel sesto problema egli definiva il calcolo delle probabilità come una "disciplina fisica" in cui "già oggi la matematica svolge un ruolo preminente" e che pertanto avrebbe dovuto essere assiomatizzata. Quale fosse il campo di applicazione della probabilità cui Hilbert faceva riferimento, sviluppatosi solo molto dopo Laplace, è indicato dal suo auspicio che l'analisi logica degli assiomi del calcolo delle probabilità potesse andare di pari passo con "un significativo e soddisfacente sviluppo del metodo dei valori medi nella fisica matematica, in particolar modo nella teoria cinetica dei gas" (Hilbert 1900, p. 295). Radicalmente diverso da quello di Hilbert era il modo di intendere la natura e i contenuti del calcolo delle probabilità di Emanuel Czuber (1851-1925), professore della Technische Hochschule di Vienna. Quale esponente tra i più stimati della disciplina in area tedesca, Czuber aveva pubblicato nel 1899 ‒ nell'ambito di una serie di compendi sulle singole branche della matematica promossa dall'Associazione dei matematici tedeschi ‒ una relazione sull'origine della teoria della probabilità e sulle sue applicazioni (Die Entwicklung der Wahrscheinlichkeitsrechnung und ihre Anwendungen). La relazione di Czuber si soffermava soprattutto sugli sviluppi della teoria della probabilità a partire da Laplace, senza far cenno alle applicazioni nel campo della fisica, in particolare nella teoria cinetica dei gas. Benché all'epoca molti fisici, seguendo Ernst Mach (1838-1916), respingessero la teoria cinetica dei gas, va detto che i suoi principali sostenitori ‒ Rudolf Clausius, James C. Maxwell e Ludwig Boltzmann ‒ che pure vedevano in essa un nuovo campo di applicazione del calcolo delle probabilità, nei loro lavori apparsi a partire dalla seconda metà dell'Ottocento non fornirono alcun contributo a questa disciplina. Perlomeno nei loro primi scritti, essi giustificavano il passaggio dal comportamento totalmente irregolare delle singole molecole ai moti regolari descritti dalle leggi dei gas richiamandosi a risultati non meglio precisati del calcolo delle probabilità. Ma anche nei successivi lavori di Boltzmann sulla teoria cinetica dei gas, nei quali venivano utilizzati modelli assai più complessi, non era ben chiaro se e in quale misura le condizioni presupposte dai teoremi della teoria probabilistica valessero anche per il modello fisico considerato. La divisione del campo di applicazione degli studi tra fisica e teoria delle probabilità propugnata dagli esponenti della teoria cinetica dei gas chiarisce come mai Czuber non facesse alcun riferimento a quest'ultima nella sua relazione del 1899, e spiega altresì il desiderio di Hilbert di colmare i vuoti che si erano creati.
Con la conferenza tenuta da Hilbert nel 1900, evento conclusivo di una tendenza già in atto precedentemente, Laplace e il suo programma contenuto nella Théorie avevano perso ogni importanza per il successivo sviluppo del calcolo delle probabilità. Testimonianze di questo crollo sono peraltro rintracciabili già nei trattati di Bertrand e di Poincaré. Nel suo Calcul des probabilités del 1888, basato su un ciclo di lezioni tenute al Collège de France, Bertrand affermava per esempio, con una certa ambiguità, che la bella opera di Laplace era forse una delle ragioni per cui il calcolo delle probabilità costituiva uno dei rami più affascinanti e nello stesso tempo più trascurati della matematica. A differenza di Laurent, Bertrand non mirava più a fornire le basi per una migliore comprensione di Laplace, tanto più che, in contrasto con quest'ultimo e in accordo con il programma di rigore matematico inaugurato da Cauchy, riteneva necessario perseguire da un lato la massima semplicità possibile nella scelta dei metodi matematici, e dall'altro lato un rigore che consentisse un'esatta valutazione della certezza e dell'ambito di validità dei risultati ottenuti. Nel Calcul des probabilités di Poincaré, pubblicato nel 1897, manca qualsiasi riferimento al ruolo di modello della Théorie di Laplace.
Il vuoto creatosi tra il 1843 e il 1873 nella letteratura francese sul calcolo delle probabilità, strettamente connesso all'influsso dell'opera di Laplace, si può spiegare in parte con l'influenza relativamente scarsa che hanno avuto le Recherches sur la probabilité des jugement di Poisson, edite nel 1837, di cui Charles Gouraud (1823-?) ha illustrato le ragioni in una storia sul calcolo delle probabilità del 1848. Secondo Gouraud, a preparare il terreno al tentativo di applicare il calcolo delle probabilità alle decisioni giudiziarie e alle testimonianze, compiuto da Poisson nelle Recherches, erano state le idee e i principî teorici di Marie-Jean-Antoine-Nicolas Caritat de Condorcet (1743-1794) e di Laplace. A differenza dei suoi predecessori, Poisson poteva disporre di una grande quantità di dati del Compte général de l'administration de la justice en France, pubblicato annualmente a partire dal 1825. I comptes généraux riportavano informazioni sul numero e sul tipo dei reati, sul rapporto tra il numero degli imputati e quello dei verdetti di colpevolezza e quindi delle condanne, sulla frequenza delle pene comminate nonché, in pubblicazioni successive, sull'età e sul sesso degli imputati o dei condannati, sul numero dei giurati ritenuti idonei per il loro incarico, sui probabili motivi dei delitti capitali, sulla recidività e sul numero delle condanne emesse con la maggioranza minima di 5 giurati su 7 prescritta all'epoca dalla legge.
Partendo dai dati dei comptes généraux, nel quinto capitolo delle Recherches Poisson cerca di applicare il calcolo delle probabilità alle decisioni giudiziarie, analizzando per esempio la probabilità che "un imputato sia condannato o assolto con la maggioranza prescritta dai voti dei giurati, ognuno dei quali ha una determinata probabilità di nonessere in errore, considerando la probabilità egualmente data della colpevolezza dell'imputato sussistente prima del giudizio" (Poisson 1837a [1841, p. XVIII]).
Nelle Recherches, dunque, conformemente al programma di applicazione universale propugnato da Laplace, Poisson aveva cercato di estendere il calcolo delle probabilità all'ambito prima inaccessibile della giurisprudenza. Completamente inattesa fu la reazione tutt'altro che concorde dei matematici a una conferenza sull'argomento tenuta da Poisson nel 1835 all'Académie des Sciences. A quanto riferisce Gouraud, per esempio, alcuni matematici dell'Académie rifiutarono l'idea di un'applicazione universale del calcolo delle probabilità, giudicandola poco seria sul piano scientifico e in grado di compromettere il prestigio della matematica. Pierre-Charles-François Dupin (1784-1873), a nome delle sezioni congiunte di analisi ed economia, dichiarò false e inutili tali applicazioni, basate su un'inaccettabile semplificazione delle situazioni reali, e Louis Poinsot (1777-1859) giunse persino a definirle una sorta di imbroglio intellettuale, in quanto l'ambito del sociale era troppo complesso perché i suoi effetti potessero essere previsti sulla base di un qualche modello matematico. A sostegno del suo radicale rifiuto dell'applicazione del calcolo delle probabilità all'ambito delle decisioni umane, che rispecchiava sostanzialmente l'atteggiamento dei filosofi dell'epoca, Poinsot poteva addurre persino un ammonimento di Laplace contro le applicazioni sconsiderate del calcolo delle probabilità all'ambito morale.
L'unanime rifiuto delle idee di Poisson da parte dei filosofi francesi, osserva sempre Gouraud, era del tutto in linea con le critiche mosse in passato ai predecessori dello stesso Poisson. Nel 1827, per esempio, il filosofo Royer Collard (1763-1845), successore di Laplace all'Académie Française, nel suo discorso inaugurale aveva condannato energicamente l'applicazione del calcolo delle probabilità ai fenomeni sociali propugnata dal suo predecessore, affermando che le motivazioni del comportamento umano sono destinate a restare avvolte nel mistero in ragione della loro complessità. Nel suo lavoro più noto al pubblico, l'Essai philosophique sur les probabilités (1814), Laplace aveva esplicitamente asserito la necessità di adottare anche nel campo sociale quell'associazione di osservazione e teoria matematica che si era rivelata tanto feconda nelle scienze naturali, attraverso l'applicazione della statistica e del calcolo delle probabilità ‒ che soltanto più tardi sarebbero diventate due discipline distinte ‒ al fine di "non opporre inutili e spesso pericolosi ostacoli all'inarrestabile progresso dell'illuminismo".
Dopo la pubblicazione delle Recherches di Poisson, Victor Cousin (1792-1867), allievo di Collard e all'epoca decano dei filosofi francesi, sulla scia delle critiche espresse dall'Académie des Sciences condannò le idee di Poisson "in nome del sacro diritto alla libertà".
L'opposizione dei filosofi francesi a Poisson era dettata da vari motivi: dal timore che lo sconfinamento della matematica fuori dai suoi limiti avrebbe potuto comportare una restrizione dell'ambito di competenze della filosofia, al conflitto tra l'orientamento politico liberale, per esempio di un Cousin, e all'attegiamento conservatore dei sostenitori di un'applicazione onnicomprensiva della matematica come Poisson. Se l'opposizione dei filosofi all'applicazione indiscriminata del calcolo delle probabilità in riferimento a Poisson ebbe un esito diverso rispetto a quanto era accaduto ai suoi predecessori, ciò si deve soprattutto al fatto che in questo caso i matematici più influenti erano solidali con i filosofi. All'origine di questo mutato atteggiamento vi era l'erosione, iniziata già negli anni Venti del secolo, del predominio assoluto esercitato sino ad allora dal modello scientifico laplaciano, erosione che consentì l'affermarsi di un nuovo stile nell'ambito della matematica e delle sue applicazioni.
Laplace aveva mutuato da Condorcet l'idea di una unificazione delle scienze naturali e delle scienze sociali nel senso più ampio, realizzata attraverso la matematica. Per attuare il progetto a essa connesso, insieme con pochi altri matematici come Jean-Baptiste-Joseph Fourier (1768-1830 ), Joseph-Louis Lagrange (1736-1813) e Gaspard Monge (1746-1818), Laplace poté sfruttare il suo grande prestigio, grazie al quale riuscì a contrastare ancora per un certo periodo le forze che si opponevano al suo programma di ricerca.
Alla divisione tra i matematici, che l'appoggio dato ai filosofi avversi a Poisson aveva reso evidente, faceva riscontro una svolta che si andava compiendo negli sviluppi della disciplina. Tale svolta può essere caratterizzata come il passaggio dalla matematica finalizzata alle applicazioni pratiche e valutata in base alla sua utilità, che dominava nelle accademie del XVIII sec., a quella insegnata negli istituti superiori come l'École Polytechnique, dove si cercava di soddisfare le esigenze didattiche richiamandosi a criteri quali il rigore e la semplicità.
Paradigma della nuova matematica divenne il Cours d'analyse di Cauchy, pubblicato nel 1821 come rielaborazione di un ciclo di lezioni introduttive all'analisi matematica tenute all'École Polytechnique. Pur riconoscendo il suo debito nei confronti della matematica del XVIII sec., Cauchy sottolineava le differenze che lo separavano dai suoi predecessori per quanto riguarda le esigenze di rigore e le idee circa le possibilità applicative della matematica. Contrariamente a quanto avevano sostenuto Laplace e in seguito Poisson, tali possibilità avevano a suo avviso dei limiti ben precisi, che venivano indebitamente trascesi da quanti intendevano applicare la probabilità matematica per valutare l'attendibilità delle asserzioni storiche o il comportamento degli uomini in determinate situazioni.
La rigorosa delimitazione dell'ambito di applicazione della matematica costituisce una caratteristica essenziale del programma di Cauchy. Egli riteneva che, fissando i limiti, per esempio, del dominio di definizione di una funzione, del dominio di convergenza delle serie e in generale dell'ambito di validità degli enunciati matematici, sarebbe stato possibile liberare la matematica dalle difficoltà causate nel secolo precedente dalle pretese di validità e di applicabilità universali.
Allorché Poisson nel 1837 riprese l'idea di Laplace di un'applicabilità universale del calcolo delle probabilità, molti matematici avevano già aderito al programma riformatore di Cauchy ed erano pertanto pronti a criticare le Recherches, che non soddisfacevano tali esigenze di rinnovamento.
Questa "nuova e inaudita" scissione, come la definisce Gouraud, che si creò tra i matematici francesi ebbe ripercussioni assai negative sul prestigio della teoria della probabilità e sull'interesse per essa in Francia. Messa di fronte alla scelta tra la Théorie e le Recherches, la maggioranza dei matematici francesi optò per la prima. Così Poisson, l'unico serio concorrente di Laplace nel determinare l'indirizzo di sviluppo del calcolo delle probabilità, ne uscì ampiamente sconfitto. Vi fu tuttavia, anche dopo Poisson, un esiguo gruppo di matematici che, indifferente alle polemiche degli anni 1836-1837, applicò la probabilità matematica alle decisioni giudiziarie e alle testimonianze, ma ‒ se si prescinde da questa minoranza ‒ il calcolo delle probabilità, dopo le aspettative suscitate da Laplace, aveva perso il suo campo di applicazione più interessante, e altre applicazioni da lui prefigurate apparivano perlomeno azzardate. A parte i metodi analitici impiegati da Laplace e da Poisson, non restava praticamente null'altro che, dopo Poisson, potesse giustificare la scelta di un giovane matematico francese di dedicarsi allo studio del calcolo delle probabilità, e ciò spiega il vuoto di almeno trent'anni verificatosi nella trattatistica francese intorno alla metà dell'Ottocento.
I numerosi richiami a Laplace in questo periodo dimostrano come dopo di lui, o meglio dopo la pubblicazione delle Recherches di Poisson, il calcolo delle probabilità classico, nato dall'applicazione del concetto di probabilità formulato da Jakob I Bernoulli (1654-1705) al gioco d'azzardo, avesse perso gran parte del suo interesse scientifico. La materia, come dimostra il trattato di Laurent, continuò a essere studiata fino al XX sec. in forma modificata rispetto a quella laplaciana, grazie soprattutto alla teoria degli errori che conservava inalterato il suo interesse scientifico ed era divenuta indispensabile nell'astronomia e nella geodesia.
I risultati e i metodi della teoria degli errori ebbero un ruolo di primo piano anche per la nascita della genetica nell'ambito della scuola biometrica inglese. Relativamente presto, tuttavia, si affermò l'idea che per le ricerche sull'ereditarietà il concetto di errore fosse del tutto inappropriato e che per stabilire la distribuzione di uno o più caratteri all'interno di una popolazione e darne una rappresentazione matematica si rendessero necessari metodi diversi da quelli offerti dalla teoria degli errori.
L'Essai philosophique di Laplace ha forse contribuito anche alla sopravvivenza del concetto classico di probabilità e indusse molti lettori a cimentarsi con la trattazione matematica della Théorie. Le ultime pagine dell'Essai dimostrano con quale abilità Laplace riuscisse a presentare il calcolo delle probabilità, che per lui, essenzialmente, non era altro che "il buon senso ridotto a calcolo", lo strumento più idoneo a soddisfare il desiderio borghese di ascesa sociale e di successo. Poiché il calcolo delle probabilità, afferma Laplace, che aveva già dato importanti contributi all'analisi matematica e alle istituzioni pubbliche, può essere d'ausilio nei problemi decisionali anche in situazioni che non consentono calcolo alcuno, "si vedrà che non esiste altra scienza maggiormente degna della nostra riflessione e che possa essere introdotta con maggior profitto nell'insegnamento" (Laplace 1878-1912, VII, p. CLIII).
Tuttavia allorché i lettori dell'Essai, testo sostanzialmente privo di formule matematiche, si cimentavano con la Théorie, si scontravano con difficoltà matematiche per i più insormontabili. Per questo motivo molti autori, spinti da considerazioni di interesse economico o di utilità didattica, si accinsero a scrivere manuali introduttivi alla Théorie o, come nel caso di Augustus De Morgan (1806-1871), trattati sostitutivi. Pertanto, sin quasi alla fine dell'Ottocento la maggior parte della letteratura sul calcolo delle probabilità ha avuto un carattere puramente didattico di introduzione alla Théorie o è stata dedicata ad alcune applicazioni opportunamente scelte tra quelle in essa trattate. I trattati in questione hanno cercato di mettere a frutto i progressi dell'analisi matematica, per esempio per sostituire il metodo delle funzioni generatrici di Laplace, caduto pressoché nell'oblio a quanto afferma Laurent, o per dimostrare i teoremi di Laplace e di Poisson con altri metodi più rispondenti alle crescenti esigenze di rigore matematico. Così Laurent introdusse nel calcolo delle probabilità i risultati sulle serie trigonometriche elaborati da Fourier e Peter Gustav Lejeune Dirichlet (1805-1859), mentre Cauchy sfruttò le possibilità offerte dalla teoria delle funzioni. Questi tentativi di perfezionare i metodi analitici del calcolo delle probabilità, che naturalmente rappresentavano anche una forma di ricerca, furono possibili grazie alle funzioni caratteristiche, la cui importanza centrale nel calcolo delle probabilità venne messa in luce soltanto nel 1925 da Paul Lévy (1886-1971) nel suo Calcul des probabilités.
In ogni caso, i risultati e i metodi del calcolo delle probabilità classico, qual era stato sviluppato da Laplace e da Poisson, furono pur sempre sufficienti a dischiudergli un nuovo campo di applicazione ‒ perlopiù ignorato dai rappresentanti della disciplina ‒ nella teoria cinetica dei gas. Il concetto, introdotto da Clausius nel 1858, di cammino libero medio di una molecola in un volume di gas a data pressione e temperatura è costruito in modo analogo a quello di durata media della vita di una data popolazione adottato da tempo nella matematica delle assicurazioni. Per la distribuzione delle velocità delle molecole di un gas, Maxwell prese in larga misura a modello la distribuzione normale considerata valida nella teoria degli errori. La teoria cinetica dei gas in seguito si è distaccata rapidamente dal calcolo delle probabilità, approdando alla meccanica statistica come disciplina autonoma. Il trattato Elementary principles in statistical mechanics sui fondamenti matematici della meccanica statistica pubblicato nel 1902 da Willard Gibbs (1839-1903), in cui viene formulato il concetto centrale di spazio delle fasi, ormai non aveva più alcun rapporto con il calcolo delle probabilità classico.
Tuttavia, per i fisici che si opponevano all'abbandono di una conoscenza della Natura apparentemente certa, in favore di proposizioni 'solo probabilmente' vere, il concetto di probabilità e la legge dei grandi numeri continuarono ad avere un ruolo decisivo nella giustificazione dell'impiego dei metodi probabilistici nella teoria cinetica.
Il mutamento dei concetti di probabilità e di caso da Laplace a Poincaré
Grazie allo sviluppo di nuovi campi di applicazione, quali la teoria cinetica dei gas e la statistica, il concetto di probabilità conobbe un profondo mutamento rispetto a quello definito da Laplace, che peraltro ha continuato a sussistere per lungo tempo accanto alle nuove formulazioni. Al perdurare della concezione laplaciana, perlomeno tra i matematici e i fisici, contribuì anche il fatto che dopo la metà dell'Ottocento quasi tutti i testi dei matematici presentavano la teoria classica della probabilità senza preoccuparsi di analizzare il significato del concetto. La discussione sulla nozione di probabile venne monopolizzata dai filosofi, che percepivano le pretese di applicazione indiscriminata del calcolo delle probabilità come un'usurpazione del proprio ambito di competenze.
La concezione della probabilità di Laplace è inscindibilmente legata alla sua visione deterministica del mondo. Per illustrare la natura di tale determinismo, egli ricorreva all'idea di un'intelligenza fittizia, il demone di Laplace, che può essere visto come il residuo di un Dio creatore nell'Universo di un ateo illuminato. Dando come tacitamente ammesso il presupposto che tutti gli eventi del Cosmo siano regolati dalla legge di causalità, questa intelligenza superiore, unicamente sulla base della conoscenza dello stato globale del Cosmo in un determinato istante, sarebbe in grado di descriverne tutti gli stati passati e futuri. Secondo Laplace il determinismo assoluto non regnava soltanto nel macrocosmo studiato dalla meccanica e dall'astronomia, ma anche nel microcosmo, ancora completamente inaccessibile alla scienza dell'epoca. La conoscenza e la capacità di previsione del demone di Laplace erano da considerarsi un limite, al quale la conoscenza umana poteva avvicinarsi soltanto asintoticamente. Laddove nella meccanica e nell'astronomia si era già giunti abbastanza vicino a questa condizione ideale, in quasi tutti gli altri ambiti mancavano conoscenze sufficienti sui rapporti causali. In tutti i campi in cui le conoscenze di cui dispone l'uomo non sono sufficienti a formulare asserzioni esatte interviene, secondo un celebre passo di Laplace, la teoria della probabilità, che è in rapporto "in parte con questa ignoranza, in parte con le nostre conoscenze". Così, nonostante Laplace fosse convinto che "la curva descritta da una semplice molecola d'aria o di gas è regolata in modo altrettanto certo quanto le orbite dei pianeti", data la nostra ignoranza, la fisica dei gas può essere trattata solamente con lo strumento del calcolo delle probabilità.
Come emerge già in uno dei suoi primi lavori sulla théorie des hasards e come verrà ribadito in seguito nell'Essai, che tanta influenza avrebbe esercitato sui suoi successori, il concetto di probabilità sotteso al determinismo di Laplace dipende dallo stato delle informazioni del soggetto umano. La probabilità di un evento misura il grado di fiducia che un soggetto razionale, sulla base delle informazioni di cui dispone al momento, ha sul suo verificarsi.
Tuttavia, poiché Laplace, conformemente alla psicologia associazionistica del XVIII sec., riteneva che il sapere e la sua elaborazione razionale da parte dell'uomo nella sede dell'intelletto, da lui chiamata sensorium, fossero oggettivabili, non lasciava alcuno spazio alla valutazione soggettiva nella determinazione della probabilità matematica. Secondo la definizione di Laplace, considerato un determinato insieme di eventi elementari ‒ nel gioco dei dadi questi sono rappresentati dalle sei facce o dai punteggi ‒ sui quali "siamo in egual misura incerti", la probabilità di un evento, per esempio la probabilità di ottenere una cifra divisibile per tre nel lancio di un dado, è data dal rapporto tra il numero degli eventi elementari favorevoli al suo verificarsi e il numero di tutti gli eventi elementari ‒ ossia, nel nostro esempio, dal rapporto tra due, il numero di casi favorevoli 3 e 6, e sei, il numero di tutti i casi possibili.
Allo scopo di illustrare la sua concezione della probabilità, Laplace utilizzava il modello di un'urna riempita con palline bianche e nere; dopo un certo numero di estrazioni casuali, con reimmissione delle palline estratte, sarebbe possibile scoprire il rapporto predefinito ma ignoto tra le palline bianche e quelle nere. Il fatto che con un numero limitato di estrazioni il rapporto trovato si discosti, in misura maggiore oppure minore, da quello effettivo dipenderebbe secondo Laplace dall'intervento di cause variabili, ossia da quello che comunemente viene chiamato 'il caso'. Attraverso il calcolo delle probabilità egli riteneva di essere in grado di dimostrare che gli effetti delle cause variabili sono ampiamente compensati da un numero elevato di prove e che pertanto "le relazioni tra gli effetti della Natura sono pressoché costanti, quando questi effetti sono considerati in grande numero". Secondo Laplace, dunque, era perfettamente legittimo ampliare il campo di applicazione del calcolo delle probabilità, che in sostanza sarebbe "soltanto il buon senso che è ridotto a calcolo", includendovi oltre ai giochi d'azzardo e alle lotterie, il calcolo degli errori in astronomia, geodesia e fisica, la statistica demografica e le assicurazioni, le decisioni politiche e giudiziarie, nonché la storia, di cui a suo avviso sarebbe possibile scoprire le leggi che ne regolano il corso.
In uno dei suoi primi scritti Laplace aveva definito il caso, che in seguito spiegherà come effetto di cause variabili, come mancanza di regolarità, come indeterminatezza e ignoranza delle cause reali. Il caso, concludeva, non ha in effetti alcun ruolo nei processi del mondo reale, non essendo altro che un "concetto per descrivere la nostra ignoranza sul modo in cui le diverse componenti di un fenomeno sono connesse tra loro e con il resto del cosmo". Il caso, secondo Laplace, non è affatto una limitazione del determinismo, poiché tale concetto non esprime altro che l'ignoranza dei nessi causali di un mondo in cui il corso dei fenomeni è ordinato sin nelle minime entità.
Nel suo Calcul des probabilités Poincaré ritiene paradossale, e quindi da spiegare, il fatto che una teoria che si basa in una certa misura sulle casualità, e di conseguenza sulla nostra ignoranza, sia ciononostante in grado di giungere a enunciati ben confermati, come accade nel caso della teoria cinetica dei gas. In Poincaré troviamo un'analisi del caso, in un Cosmo anche per lui deterministicamente ordinato, che sintetizza gran parte della discussione sui concetti di caso e di probabilità dopo Laplace.
Consideriamo un cono che stia in equilibrio instabile sul vertice: è sufficiente la minima turbolenza nell'aria circostante per spostarne il baricentro e farlo cadere. Da questo esempio desunto da Cournot, Poincaré trae la sua più importante caratterizzazione del caso, inteso come una sorta di leva tra causa ed effetto: piccole variazioni nelle cause possono provocare grandi mutamenti negli effetti. Di conseguenza, anche se conoscessimo tutte le leggi della Natura necessarie a fornire una descrizione completa dei processi nel Cosmo, non saremmo egualmente in grado di formulare previsioni esatte sullo stato di un sistema nel futuro; la determinazione delle grandezze e dei parametri necessari allo scopo, infatti, sarà sempre inficiata da errori. Se dunque, dato l'effetto di leva che la causa ha per l'effetto, il margine di variazione di quest'ultimo (dovuto all'errore nella determinazione della causa) è troppo grande, ogni previsione esatta diventa impossibile. L'effetto, allora, appare come un evento casuale. In tal modo, per citare un altro esempio utilizzato in seguito da Poincaré, anche il più abile lanciatore di coltelli, a partire da una determinata velocità di rotazione del bersaglio, non sarà più in grado di colpire un suo punto prestabilito, dal momento che variazioni minime nelle condizioni che determinano il lancio del coltello inducono grandi variazioni nell'esito del lancio stesso.
Un altro aspetto del caso riguarda il numero dei fattori che influenzano il verificarsi di un evento. Poincaré citava come esempio la teoria cinetica dei gas, in cui i fattori generatori di casualità ‒ i piccoli mutamenti nelle cause che provocano un grande mutamento negli effetti ‒ sono da un lato i singoli urti tra le molecole o tra le molecole e le pareti del recipiente, dall'altro il numero di questi urti in piccolissimi intervalli di tempo. Se per esempio la variazione media della direzione del moto di una molecola di gas, dovuta all'urto con un'altra molecola o con le pareti del recipiente, ha il valore A, dopo un numero n di urti assumerà il valore An, dove n è un numero che può assumere valori molto grandi. Analogamente, la distribuzione apparentemente casuale di particelle pulviscolari nei liquidi, dei diversi pigmenti nei miscugli di liquidi o di polveri di diverso colore, delle carte quando si mescola un mazzo e dei cosiddetti 'errori casuali' dipende da una molteplicità di fattori diversi.
Un altro modo in cui si genera il caso, che già Cournot considerava essenziale e che troviamo menzionato per la prima volta in Aristotele, è l'intersecarsi nello spazio e nel tempo di due serie di eventi apparentemente indipendenti ma tra loro connesse causalmente; è quanto accade, per esempio, quando un individuo che percorre una strada con un determinato proposito si trova a passare esattamente nel punto e nel momento in cui una tegola malferma cade da un tetto, colpendolo. Secondo Poincaré, tuttavia, questo terzo modo in cui si verificano eventi che appaiono casuali, in molti casi può essere ricondotto ai primi due.
Spiegato il fatto che la casualità, derivante da grandi effetti di piccole cause o dalla complessità di molti fattori che si influenzano reciprocamente per un gran numero di ripetizioni, mostra la stabilizzazione delle frequenze relative dedotta dal calcolo delle probabilità, Poincaré può a questo punto interrogarsi sull'oggettività del concetto di caso. A questo riguardo, egli ammette che gli aggettivi 'piccolo' e 'complesso' utilizzati nella sua definizione del caso hanno solamente un valore relativo, ma precisa che piccolo e complesso sono relativi non in rapporto allo stato delle conoscenze del soggetto umano, bensì in rapporto allo stato del Cosmo in un determinato istante, e pertanto sono, dal punto di vista umano, oggettivi.
L'oggettività degli eventi casuali postulata da Poincaré non è in contraddizione con la sua visione deterministica del mondo, poiché l'esatta determinazione di tutti i dati necessari alla previsione di un evento è in pratica impossibile.
Molto prima di Poincaré, matematici come Poisson e Cournot avevano cercato di dare una dimensione oggettiva al concetto di probabilità adottato da Laplace, dipendente dallo stato delle conoscenze del soggetto umano.
Lo stesso Laplace nei primi scritti aveva considerato altri aspetti del probabile, che poi non avrebbe ripreso in questa forma nell'Essai. Nel Mémoire sur les probabilités del 1781 egli aveva distinto tre tipi di determinazione della probabilità, che si rifacevano ancora a una tradizione risalente a Jakob I Bernoulli: la determinazione a priori, come nel lancio di una moneta o dei dadi, sulla base del calcolo combinatorio e della simmetria fisica degli eventi elementari; la determinazione a posteriori, che si basa sulla frequenza relativa di un evento per un numero elevato di ripetizioni; e infine, la determinazione basata sulle conoscenze di cui dispone il soggetto, come avviene per esempio quando si stima la forza di due giocatori sulla base delle informazioni sui loro successi in incontri precedenti o sulle loro attuali condizioni fisiche e psichiche. I primi due casi, conformemente alla distinzione introdotta da Poisson e da Cournot tra probabilità oggettiva e probabilità soggettiva, rientrano nella categoria della probabilità oggettiva. Nel terzo caso ‒ che fa riferimento al grado di fiducia che un individuo, sulla base delle conoscenze di cui dispone in un determinato momento, nutre nel verificarsi di un evento ‒ siamo invece in presenza di una probabilità 'soggettiva', termine che peraltro Laplace non usa.
Successivamente, sino alla redazione dell'Essai, egli adottò l'idea che la probabilità, anche nelle due forme che in seguito saranno definite 'oggettive', dipende sostanzialmente dalle informazioni di cui dispone il soggetto. Tuttavia nel caso delle probabilità a priori e a posteriori si tratta di informazioni oggettivabili: fornite a matematici diversi, indipendentemente dalle loro caratteristiche personali, esse condurrebbero sempre agli stessi valori. In tal modo, la probabilità di estrarre una pallina nera dalla prima di tre urne contrassegnate dai numeri 1, 2 e 3 e delle quali una contiene soltanto palline nere e le altre due solo palline bianche, verrà valutata in modo diverso a seconda che si disponga dell'informazione supplementare che la seconda urna contiene soltanto palline bianche, o la prima solamente palline nere. Le stime della probabilità che dipendono dalle nostre conoscenze sono però completamente indipendenti da caratteristiche personali soggettive.
Nell'Essai invece, in relazione ai motivi che inducono i singoli individui a credere nel verificarsi di un dato evento, Laplace, richiamandosi ai meccanismi postulati dalla psicologia associazionistica del XVIII sec., cerca di spiegare la formulazione di valutazioni 'false' del probabile con caratteristiche puramente personali, quali l'interesse o il gusto. Poiché nella ricezione delle idee di Laplace l'Essai ha avuto un ruolo determinante, molti si convinsero che Laplace considerasse solamente un aspetto della probabilità percepito come soggettivo , o che perlomeno la tesi secondo cui la probabilità dipende dalle conoscenze a disposizione dell'individuo potesse essere fraintesa in senso esclusivamente soggettivo. In ogni caso si avvertiva la necessità di fornire anche una definizione oggettiva della probabilità.
Poisson operò dunque una distinzione tra chance, intesa come probabilità completamente indipendente dalle conoscenze di cui dispone il soggetto oppure dalla sua fiducia nel verificarsi di un evento, e probabilité, intesa invece come probabilità "individuale, soggettiva, legata a una determinata persona".
La legge dei grandi numeri di Poisson e le sue precisazioni attraverso le varie forme del teorema del limite centrale, per cui per esempio all'aumentare delle prove la frequenza relativa di un evento tende a stabilizzarsi, o i tassi di natalità annuali in una popolazione sufficientemente ampia tendono a essere costanti, era orientata a un'interpretazione della probabilità come 'chance', ossia come una grandezza che dipende esclusivamente da fatti oggettivi, come per esempio l'omogeneità e la forma di un dado. Tale grandezza indica la frequenza di un evento in una serie di prove ripetute, o di una determinata caratteristica in una data popolazione. Tuttavia la frequenza con cui si ottiene un sei in 60 lanci con un dado perfetto non deve necessariamente cadere nell'intervallo tra 8 e 12 intorno al valore atteso 10, ma potrebbe cadere anche al di fuori di tale intervallo con una probabilità calcolabile che può essere interpretata, anche secondo Poisson, come grado di aspettativa di un soggetto razionale nel verificarsi di quest'ultima eventualità. Il concetto di probabilità in Poisson comprende entrambi gli aspetti, ora differenziati anche terminologicamente: quello soggettivo, relativo al grado di fiducia con cui un soggetto, sulla base delle conoscenze che possiede, è disposto a credere in un'asserzione, e quello oggettivo, relativo alla frequenza con la quale un determinato evento si verifica in una serie di prove ripetute.
Cournot rafforzò ulteriormente la distinzione tra probabilità oggettiva e soggettiva, fondando la sua concezione della probabilità oggettiva su un'attenuazione del determinismo di Laplace. Egli prendeva anche le distanze dall'idea di una universalità delle applicazioni della matematica e della meccanica, ed esprimeva in particolare la convinzione che le decisioni e i processi mentali umani non si sarebbero mai potuti ricondurre a questi ambiti.
Cournot limitava la validità della legge di causalità (e quindi del determinismo) attuando una distinzione tra serie di eventi dipendenti o indipendenti. Nel primo caso due eventi che si succedono immediatamente l'un l'altro stanno in un rapporto di causa ed effetto, dove l'effetto diventa a sua volta causa dell'evento immediatamente successivo. Inoltre, nelle serie causali dipendenti, un evento non dipende da un'unica causa, bensì da tutti gli eventi che lo precedono nella serie. Accanto alle serie causali dipendenti vi sono quelle indipendenti. Può accadere però che in due serie causali indipendenti si verifichi nello stesso momento lo stesso evento; si ha allora quello che Cournot definisce un evento casuale.
Per illustrare questo concetto Cournot porta l'esempio di due fratelli che vengono uccisi nello stesso momento in un'azione militare. Fattori come l'affetto del fratello minore che sceglie di fare il soldato seguendo le orme del fratello più grande e gli resta vicino in battaglia, renderebbero la morte contemporanea dei fratelli un evento appartenente a due serie dipendenti e dunque spiegabile in termini causali. Se avvenisse in due teatri di guerra geograficamente molto distanti, la morte contemporanea dei due fratelli andrebbe invece considerata come un evento appartenente a due serie indipendenti, e dunque come un evento casuale.
Il fatto che un cono resti in equilibrio sul vertice, così come l'estrazione di una pallina nera da un'urna che contiene un'unica pallina nera e innumerevoli palline bianche, è un evento assolutamente casuale. Un evento di questo tipo, la cui probabilità in senso classico è 'infinitamente piccola', viene considerato da Cournot fisicamente impossibile, che soltanto con "la teoria matematica della probabilità acquista un significato oggettivo nel mondo reale". Poiché secondo la legge dei grandi numeri la frequenza relativa di un evento in un numero infinitamente grande di osservazioni diventa arbitrariamente prossima alla sua probabilità, la probabilità di uno scostamento anche minimo della frequenza relativa dalla probabilità dell'evento è infinitamente piccola e quindi fisicamente impossibile.
Il tentativo di Cournot ‒ per certi versi artificioso ‒ di giustificare la necessità di una probabilità oggettiva, in parte presuppone tacitamente ciò che egli intende dimostrare. Si ha qui una testimonianza della fede incrollabile di Cournot nell'esistenza di un caso e di una probabilità oggettivi, dipendenti soltanto da fattori reali, che non si basa più sulla visione deterministica del mondo di Laplace. In effetti, per Cournot i poteri di un'intelligenza sovrumana, a differenza di quanto accadeva per il demone di Laplace, potrebbero non andare oltre la capacità di prevedere le frequenze relative di un evento in un numero elevato di prove. Ciò non significava un abbandono definitivo della causalità e del determinismo nella teoria matematica della probabilità; tuttavia un lettore di Cournot, magari sotto l'influsso degli scritti di Quételet, di Charles Darwin (1809-1882) o di Francis Galton (1822-1911), di fronte alla crescente quantificazione della società attraverso gli uffici statistici in rapida diffusione nei paesi europei e all'affermarsi dei metodi probabilistici nella fisica, avrebbe potuto considerarlo come sostenitore di una concezione non deterministica e, forse, sentirsi indotto ad abbandonare il determinismo.
Il filosofo e matematico americano Charles S. Peirce (1839-1914) aveva già deciso di compiere questo passo. Come spiega in vari scritti risalenti agli anni Novanta del secolo, rifiutando il determinismo aveva adottato una definizione oggettiva della probabilità basata sul concetto di frequenza per descrivere gli eventi in un Cosmo completamente indeterministico. Secondo Peirce, che nella sua attività più che ventennale per la US Coast Survey aveva condotto numerosi esperimenti di fisica con strumenti spesso progettati da lui stesso, il punto di partenza della revisione e in seguito della negazione del determinismo era stata la teoria degli errori.
Il metodo dei minimi quadrati
All'origine del grande interesse suscitato dalla teoria degli errori nel calcolo delle probabilità del XIX sec. vi è la scoperta del metodo dei minimi quadrati. La sua prima comparsa, in uno scritto pubblicato da Adrien-Marie Legendre (1752-1833) nel 1805, diede luogo poco dopo a una controversia con Carl Friedrich Gauss che si protrasse per diversi anni.
In un'appendice al suo scritto sulla determinazione dell'orbita delle comete del 1805, intitolato Sur la méthode des moindres quarrés, Legendre aveva proposto una soluzione al problema di ottenere risultati quanto più possibile esatti da una serie di misurazioni di una grandezza. Sulla base di una linearizzazione, illustrata con l'esempio della determinazione dello schiacciamento della Terra attraverso le misurazioni della lunghezza di un meridiano, Legendre aveva pensato di ricondurre il problema alla soluzione di un sistema di equazioni lineari della forma:
dove le aij come funzioni dipendenti dalle misurazioni sono coefficienti e le incognite xj sono parametri della funzione che risolve il problema di partenza. Le Ei rappresentano gli errori dovuti all'imprecisione delle osservazioni, sul cui valore si hanno soltanto informazioni contenute implicitamente nelle misurazioni di cui si dispone. Si tratta allora di sfruttare tali informazioni in modo da minimizzare gli errori Ei. A seconda che la minimizzazione riguardi il valore dei singoli errori, come nelle applicazioni dell'epoca, o la somma dei valori assoluti di tutti gli errori, oppure ancora la somma di una potenza pari degli errori, esistono diverse possibilità di sfruttare le informazioni fornite implicitamente dalle misurazioni. Legendre parte dalla considerazione che n>m, e quindi che la [1] risulti indeterminata, se si prescinde dalle Ei. Egli si propone allora di ridurre con un opportuno procedimento il sistema di equazioni [1] a un altro, in cui il numero delle equazioni sia eguale a quello dei parametri incogniti. La soluzione "più generale, più esatta e più semplice" consiste, secondo Legendre, nel rendere minima la somma dei quadrati degli errori
si ottiene la riduzione cercata a un sistema di m equazioni lineari per le m incognite xj. Si tratta delle equazioni che in seguito Gauss chiamerà equazioni normali. Con la soluzione della [3] per le xj, che qualora esista è unica, dalle n equazioni di partenza della [1] si ottengono dei valori per gli n errori Ei che corrispondono al minimo della somma dei quadrati degli errori, ma naturalmente non dicono nulla sui 'veri' errori effettivamente commessi. Se, per esempio, confrontando i valori così ottenuti per le Ei risulta che l'ordine di grandezza di uno o più errori supera considerevolmente la media, Legendre propone di ripetere il processo eliminando dal sistema originario [1] le k equazioni relative a questi errori fortemente devianti e applicando nuovamente il metodo dei minimi quadrati al nuovo sistema costituito dalle restanti n−k equazioni lineari. Sia Legendre sia Gauss utilizzarono nelle loro rappresentazioni del metodo dei minimi quadrati una forma che corrisponde alla notazione degli indici qui impiegata.
Gauss nella controversia con Legendre che seguì la pubblicazione del metodo nella Theoria motus corporum coelestium in sectionibus conicis solem ambientium del 1809, sosteneva di aver utilizzato sistematicamente il metodo dei minimi quadrati, al pari presumibilmente di molti altri, sin dagli anni Novanta del XVIII secolo. A suo avviso, la semplice menzione del metodo da parte di Legendre, dal punto di vista matematico non poteva essere paragonata a una dimostrazione di specifiche proprietà che comprovassero la sua utilità e quindi la sua legittima applicabilità.
Gauss ‒ il più importante pioniere degli algoritmi ottimali di soluzione, elaborati in funzione applicativa, per il sistema di equazioni trovato con il metodo dei minimi quadrati ‒ nella Theoria motus ne forniva anche una derivazione in termini puramente probabilistici, destinata a diventare la più usata. Sotto l'ipotesi che il valore più prossimo a quello reale della grandezza misurata sia la media aritmetica delle misure della grandezza stessa, Gauss dimostra che la distribuzione degli errori assume la forma di quella che oggi chiamiamo distribuzione normale o gaussiana, di densità
dove h è il grado di precisione delle misurazioni. In generale Gauss assume che i valori da stimare xi siano coerenti con i valori osservati νi e con gli errori di osservazione εi, con identica distribuzione normale; pertanto le somme νi+εi devono essere uguali a fi dove le fi sono le funzioni assegnate dei dati,
[5] νi +εi=fi (x1,…,xm) (i=1,…,n).
Sulla base di considerazioni equivalenti al principio della massima verosimiglianza e del presupposto di una distribuzione normale degli errori di osservazione, Gauss deduce che il "sistema di valori più probabile" delle xi possa ottenersi imponendo la condizione
Non appena Laplace venne a conoscenza di questo lavoro tentò di dimostrare la distribuzione normale degli errori, implicitamente adottata da Gauss, con un'ipotesi alternativa. In un lavoro del 1811, i cui contenuti vennero ripresi l'anno successivo con poche variazioni nella Théorie analytique des probabilités, Laplace considera nel sistema di equazioni lineari
valori stimati x*j per le xj mediante i quali le differenze x*j−xj possono essere rappresentate con appropriati moltiplicatori λi nella forma
I valori stimati secondo il metodo dei minimi quadrati soddisfano le condizioni [8]. Laplace dimostra che le combinazioni lineari di un gran numero di osservazioni con errori simmetricamente e identicamente distribuiti hanno una distribuzione approssimativamente normale, mostrando così l'ottimalità dei valori stimati con il metodo dei minimi quadrati, secondo i diversi criteri della teoria delle probabilità.
Le critiche al tentativo di fondare il metodo dei minimi quadrati sulla teoria della probabilità, nonché i lavori pubblicati nel frattempo da Laplace, indussero Gauss a presentare nel 1823 una nuova dimostrazione. Qui, analogamente a Laplace, egli considera la simmetria e la differenziabilitàrispetto a x come le uniche condizioni per la densità φ(x) di distribuzione degli errori; definisce quindi con 'grado di precisione delle osservazioni' la quantità 1/m, con 'varianza della distribuzione φ(x)' la quantità m2 data dalla relazione
e, infine, con 'errore medio delle misurazioni' la radice quadrata m della varianza come definita nella [9]. Con il principio della minima varianza Gauss trova una nuova dimostrazione del metodo dei minimi quadrati, indipendente sia dalla forma speciale della distribuzione degli errori sia dal numero delle equazioni nella [1], e pertanto l'unica a suo parere accettabile.
Ai tentativi compiuti da Laplace e da Gauss di dimostrare il metodo dei minimi quadrati con la teoria della probabilità, ne fecero seguito molti altri. Accanto agli approcci che non facevano alcun riferimento al calcolo delle probabilità, assunse un ruolo importante la cosiddetta ipotesi degli errori elementari. In particolare, i rappresentanti tedeschi della teoria degli errori come Gotthilf Heinrich Ludwig Hagen (1797-1884) e il suo insegnante, l'astronomo Friedrich Wilhelm Bessel (1784-1846) si servirono di tale ipotesi per derivare una distribuzione normale degli errori in modo diverso rispetto a Gauss. L'idea fondamentale dell'ipotesi degli errori elementari, secondo la quale ogni errore di osservazione o misurazione è la somma di un gran numero di errori elementari più piccoli e indipendenti, era già stata formulata nel XVIII sec. in forma qualitativa da Daniel Bernoulli (1700-1782). Nel 1837 Hagen partì dal modello assai semplice secondo il quale un errore elementare può assumere solo uno dei due valori molto piccoli a e −a, a≠0, ciascuno con eguale probabilità 0,5 e in cui inoltre la somma di tali errori elementari ha una distribuzione binomiale simmetrica. Bessel, che già in un lavoro del 1818 riteneva di aver dimostrato che la distribuzione normale è la 'più naturale', la più idonea cioè per tener conto degli errori nelle misurazioni astronomiche, assume come condizione per gli errori elementari solo densità simmetriche rispetto a 0 ma per il resto arbitrarie, dimostrando in un lavoro del 1838 che la distribuzione delle loro somme risulta approssimativamente normale.
Verso la fine del secolo le distribuzioni empiriche scoperte nella statistica, che si discostano in misura maggiore o minore dalla normale, spinsero a modificare l'ipotesi degli errori elementari per definire distribuzioni teoriche più adatte a queste distribuzioni empiriche non normali. I risultati decisivi in questo senso si sono avuti, peraltro, solo all'inizio del XX secolo.
Questi sviluppi si collocano nell'ambito di una teoria puramente matematica degli errori, cui le scienze applicate hanno dato importanti sollecitazioni. Per i principali fruitori della teoria degli errori del XIX sec., i geodeti e gli astronomi, dalla cui cerchia sono derivati anche i contributi più significativi agli sviluppi teorici, le controversie in parte di natura squisitamente teorica ‒ soprattutto quelle sulla validità del metodo dei minimi quadrati come strumento per la compensazione degli errori nei dati osservati ‒, apparivano assai meno interessanti del metodo stesso e del connesso apparato per la determinazione dei parametri cercati e dei relativi errori.
Con l'inserimento a opera di Gauss e di Laplace della teoria degli errori con il metodo dei minimi quadrati quale suo cardine nel calcolo delle probabilità, essa è divenuta uno dei rami più intensamente studiati dai matematici nell'Ottocento, tanto che alcuni autori finirono per identificare la teoria degli errori con il calcolo della probabilità. Per esempio, Jean-Baptiste-Joseph Liagre, nel Calcul des probabilités et théorie des erreurs pubblicato a Bruxelles nel 1852, distingueva nel titolo i due ambiti, ma nella trattazione considerava il calcolo delle probabilità come premessa teorica per le applicazioni, che costituivano la parte di reale interesse, con esclusivo riferimento alla teoria degli errori. Oltre agli autori più importanti per il campo delle applicazioni, al quale era dedicato il maggior spazio, come Sylvestre-François Lacroix, Antoine-Augustin Cournot e Quételet, Liagre menzionava, accanto a Laplace, i tedeschi Gauss, Bessel, Johann Franz Encke e Christian Ludwig Gerling.
Dagli sviluppi della ricerca inaugurata da Gauss scaturì una serie di risultati che in parte fornirono i concetti matematici di base per la statistica matematica sviluppatasi dalla scuola biometrica inglese.
Un esempio è costituito dalla dissertazione di Ernst Abbe (1840-1905) sulla casualità degli errori in una serie di misure sperimentali di una grandezza. Partendo da una serie di misure (xi,yi), con i=1,…,n, di due grandezze variabili x e y ‒ per esempio la pressione e la temperatura di un gas ‒ delle quali è nota la relazione y=f(x), Abbe considera le n differenze f(xi)−yi calcolabili direttamente dalle misurazioni, come la serie di errori da investigare. Come criterio di casualità Abbe assume la distribuzione normale degli errori. Partendo dal presupposto che i singoli errori siano indipendenti e abbiano identica distribuzione normale, Abbe dimostra che la somma dei quadrati degli errori ha distribuzione χ2 a n gradi di libertà. La somma dei quadrati degli errori viene dunque assunta da Abbe come test per verificare la casualità di errori che hanno una distribuzione normale.
Un'importanza relativamente scarsa per le applicazioni hanno avuto le varie forme del teorema del limite centrale, che sono state invece determinanti per gli sviluppi matematici del calcolo degli errori nel XIX secolo. Nel 1733 Abraham de Moivre (1667-1754) aveva stabilito un teorema limite secondo il quale una distribuzione binomiale converge a quella che in seguito sarebbe stata denominata distribuzione normale e pertanto, nel caso di un numero n sufficientemente elevato di misurazioni aventi distribuzione binomiale, si può utilizzare la distribuzione normale, più agevole da trattare numericamente. Il teorema di de Moivre era stato generalizzato da Laplace nell'ambito di numerosi problemi applicativi, soprattutto con riguardo al calcolo degli errori. Egli era andato oltre la considerazione delle serie binomiali e nel contesto della dimostrazione del metodo dei minimi quadrati o dell'utilizzazione dei valori medi nella fisica e nell'astronomia, si era interessato alla distribuzione di una somma o di una combinazione lineare di n errori. Laplace era riuscito a dimostrare che nel caso di errori aventi la stessa funzione di distribuzione o, per usare la terminologia attuale, di variabili casuali X1,…,Xn, perlopiù assunte come limitate, indipendenti e con lo stesso valore atteso μ e varianza σ2, al crescere di n la distribuzione converge alla distribuzione normale. I risultati ottenuti da Laplace nella Théorie e in lavori precedenti per variabili casuali sia discrete sia continue, non erano stati espressi nella forma di teoremi matematici divenuta corrente con Augustin-Louis Cauchy (sotto le condizioni menzionate in precedenza). Tali risultati possono essere così riassunti: per valori grandi di n la probabilità P che la somma delle n variabili casuali indipendenti, tutte con varianza σ2, si discosti dal suo valore atteso nμ di un valore dell'ordine di grandezza di √n, può essere stimata mediante la distribuzione normale
Per le derivazioni che nel singolo caso risultavano spesso assai lunghe per i calcoli, Laplace si era servito della teoria delle funzioni generatrici di argomento complesso, da lui stesso sviluppata sulla scia di de Moivre e di Lagrange, che costituisce una prima forma della teoria delle funzioni caratteristiche formulata in seguito da Poincaré. Laplace aveva cercato anche di stimare perlomeno l'ordine di grandezza approssimato dell'errore, quando nel caso di un numero finito n di misurazioni la loro somma, o una loro combinazione lineare, venga sostituita dalla distribuzione normale.
I matematici della generazione successiva concentrarono l'attenzione sulle condizioni sotto le quali una distribuzione di probabilità può essere considerata asintoticamente normale. Così Poisson, nell'ambito della generalizzazione della legge dei grandi numeri di Bernoulli, servendosi degli stessi strumenti analitici di Laplace riuscì a dimostrare, per variabili casuali Xi continue o discrete, non più necessariamente distribuite in modo identico, con valori attesi μi e varianze σ2i, l'equivalente di
Le derivazioni di varie forme del teorema del limite centrale effettuate da Laplace e da Poisson, che in base ai nuovi standard imposti da Cauchy per la formulazione e la dimostrazione di enunciati matematici apparivano discutibili, indussero quest'ultimo nel 1853 a dimostrare il teorema del limite centrale sotto condizioni decisamente più restrittive.
Questa dimostrazione fa parte di una serie di lavori di Cauchy, risalenti al 1853, dedicati alla controversia con Irénée-Jules Bienaymé sul valore e sul ruolo del calcolo della probabilità nell'edificio complessivo della matematica, con particolare riguardo al metodo dei minimi quadrati. Il contrasto tra i due matematici, in cui senza dubbio ha avuto un ruolo anche l'appartenenza a diversi schieramenti politici, fu occasionato dal fatto che Bienaymé, in un lavoro sul metodo dei minimi quadrati presentato all'Académie des Sciences nel 1852, si era pronunciato a favore della teoria della probabilità di Laplace, di cui Cauchy criticava aspramente le pretese di applicazione indiscriminata che con le Recherches di Poisson del 1837, a suo avviso, avevano trasceso ogni limite di ragionevolezza. In uno scritto del 1853, pertanto, Cauchy fece riferimento al proprio metodo, pubblicato già nel 1835, per la determinazione progressiva dei coefficienti incogniti ai di una funzione
dove le funzioni ui (x) sono note e si conoscono n coppie di valori xi dati e yi affetti da errori. Cauchy sosteneva che il suo procedimento fondato sull'analisi fosse più efficace di quello dei minimi quadrati. Nel prosieguo della discussione, dopo che Bienaymé ebbe spiegato le diverse finalità dei due metodi, Cauchy si occupò in modo più approfondito della teoria degli errori, definendo le più importanti proprietà delle funzioni caratteristiche, all'epoca non ancora note sotto questo nome. Le ricerche di Cauchy erano in larga misura svincolate dalle applicazioni pratiche e consideravano le distribuzioni degli errori e le loro proprietà in forma del tutto generale, almeno per i livelli di astrazione raggiunti dall'analisi del XIX secolo. La conclusione cui giunse Cauchy fu che il metodo dei minimi quadrati risultava più vantaggioso nel senso inteso da Laplace solo nel caso di una distribuzione normale degli errori. Nel caso di una distribuzione non normale, Cauchy affermava che anche la distribuzione di ogni combinazione lineare di tali errori deve essere non normale.
La trattazione rigorosa del calcolo delle probabilità inaugurata da Cauchy e Bienaymé fu sviluppata successivamente in due direzioni dal fondatore della scuola russa Pafnutij L´vovič Čebyšev (1821-1894), il quale diede una dimostrazione elementare completa della diseguaglianza che porta il suo nome, da lui concepita come una generalizzazione della legge dei grandi numeri di Bernoulli.
Čebyšev considerava il teorema del limite centrale come un enunciato autonomo nell'ambito del calcolo delle probabilità, completamente svincolato dalle applicazioni. Tuttavia l'intento di utilizzare il teorema del limite centrale come esempio per illustrare la sua teoria dei momenti gli fu d'ostacolo nella ricerca di condizioni di validità più deboli di quelle da lui postulate, che comprendevano ancora l'esistenza di tutti i momenti di ordine comunque grande. Maggiore successo in questa direzione ebbero invece gli allievi di Čebyšev: Andrej Andreevič Markov (1856-1922) e Aleksandr Michajlovič Ljapunov (1857-1918). In particolare Ljapunov fornì tra il 1900 e il 1901 una dimostrazione 'elementare' per la convergenza alla distribuzione normale della distribuzione di somme di variabili casuali, che richiede soltanto che siano noti il valore atteso e la varianza, e che sia rispettata la cosiddetta 'condizione di Ljapunov'.
L'interpretazione del teorema del limite centrale di Ljapunov esemplifica il riassorbimento nella matematica di una teoria della probabilità 'moderna', ampiamente svincolata dalle applicazioni. Nello stesso tempo gli aspetti concettuali del calcolo delle probabilità, in particolare quello della teoria degli errori opportunamente modificata, sono stati di importanza decisiva per gli sviluppi ulteriori della statistica, nata in seno alla scuola biometrica inglese, che in seguito all'assorbimento della teoria delle probabilità nella teoria della misura e dell'integrazione di émile Borel (1871-1956) e Henri-Léon Lebesgue (1875-1941) si è separata dal calcolo delle probabilità divenendo un campo di applicazione completamente autonomo.
Leggi dei grandi numeri
Le prime formulazioni delle leggi dei grandi numeri vennero elaborate da Laplace, sulla scia di Bernoulli, nella Théorie e in alcuni lavori precedenti. Una delle formulazioni adottate da Laplace si trova nel contesto della teoria degli errori (1812 [1878-1912, VII, p. 338]): "Se si divide la somma degli errori per il loro numero s al fine di ottenere l'errore medio, questo converge all'ascissa del centro, in modo tale che prendendo un intervallo piccolo a piacere sull'uno e sull'altro lato, la probabilità che l'errore medio in un numero illimitato di osservazioni cada in questo intervallo differisce dalla certezza meno di una grandezza piccola a piacere".
Dalle condizioni poste da Laplace discende che tutti gli errori, assunti tacitamente limitati e indipendenti, hanno la medesima distribuzione di densità φ(x) e quindi identica distribuzione di probabilità. Indicando con μ l'ascissa del baricentro della figura piana delimitata dal grafico di φ(x) e dall'asse delle ascisse risulta
μ pertanto non è altro che il valore atteso dei singoli errori. Nel linguaggio dell'analisi dei tempi di Weierstrass, indicando gli errori con εi con i =1,…,s, il teorema di Laplace afferma che, fissati comunque due numeri positivi ε e δ (con δ⟨1), esiste sempre un intero s tale che qualunque sia l'intero n≥s risulta:
Oltre alla [14], si trovano varie formulazioni, perlopiù non matematiche, della 'legge debole dei grandi numeri' nella forma dimostrata da Jakob Bernoulli. Nell'Essai si afferma che al crescere del numero delle osservazioni gli effetti casuali recedono di fronte alle "cause costanti e regolari". Tuttavia Laplace non attribuiva alla legge dei grandi numeri il peso che le attribuiva Bernoulli.
Le cose cambiarono nuovamente con Poisson, che nelle sue Recherches ampliò in modo sostanziale le condizioni di validità della legge dei grandi numeri conferendole un'importanza decisiva nell'architettura del suo calcolo delle probabilità, stabilendo l'invarianza della media aritmetica in diverse serie di osservazioni. Poisson fu il primo a introdurre il concetto di 'legge dei grandi numeri', che riguarda le frequenze "pressoché invariabili" in un numero elevato di osservazioni di eventi che "dipendono da cause costanti e da cause che variano in modo irregolare". Il verificarsi di tali cause irregolari deve chiaramente soddisfare una distribuzione simmetrica rispetto a x=0. Poisson definisce l'approssimativa invarianza delle frequenze con l'approssimativa e "altamente probabile" eguaglianza tra m/μ e m′/μ′, frequenze relative di un evento in due diverse serie di osservazioni. Per spiegare la legge dei grandi numeri egli generalizzò il concetto di causa a quella che in seguito verrà definita 'causa stocastica'.
Per esprimere la legge in forma matematica Poisson si serve di due teoremi cui attribuisce soltanto una funzione ausiliaria, ma che nel XX sec. hanno assunto il valore di leggi ('deboli') dei grandi numeri. A differenza dei suoi predecessori, Poisson non assume più l'identica distribuzione delle cause irregolari, ossia di quelle che oggi si definiscono variabili casuali. Poiché ora i valori attesi delle singole variabili casuali Xi possono non essere eguali, non si tratta più, come fa Laplace, di dimostrare che la media aritmetica di tali variabili converge in probabilità al valore atteso, bensì di dimostrare, come fa Poisson, che la media aritmetica di n variabili Xi 'converge in probabilità' alla media aritmetica dei loro valori attesi E(Xi), in altre parole, che fissato un numero ε>0 comunque piccolo, la probabilità che al crescere di n la differenza fra le due medie sia (in valore assoluto) minore di ε tende a 1:
per n→∞. Poisson generalizza la legge di Bernoulli dei grandi numeri, escludendo l'ipotesi dell'uguaglianza delle probabilità pi (con i=1,…,n) di un evento alla i-esima di n prove indipendenti e focalizzando l'attenzione sulla frequenza relativa hn. In tal caso, al crescere di n si ha:
per n→∞. Poisson tuttavia considerava non questi due teoremi, bensì la propria formulazione della legge dei grandi numeri, criticata già da vari autori del XIX sec. in quanto troppo vaga, come "applicabile a tutti gli eventi incerti del mondo fisico e morale". Egli si riferiva in particolare agli eventi demografici, che rivestono un'importanza centrale per le assicurazioni. I critici della legge dei grandi numeri formulata da Poisson attaccavano, come Bienaymé, i sistemi di cause stocastiche che egli aveva introdotto; altri mettevano in dubbio la liceità dei metodi analitici utilizzati, mentre altri ancora, come il russo Čebyšev, cercavano di valutare, per un numero finito di osservazioni la bontà dell'approssimazione della frequenza relativa al suo valore atteso nel teorema del limite centrale sopra menzionato.
Tali critiche, peraltro, non fecero grande impressione alla maggior parte degli studiosi, interessati piuttosto alle giustificazioni offerte da Poisson sull'uso di strumenti matematici, o alla sua interpretazione di una significativa differenza tra le frequenze relative di due serie di osservazioni a seguito di un mutamento delle cause.
Poisson vide negli annuari di statistica criminale, pubblicati in Francia a partire dal 1825, la migliore conferma della sua legge dei grandi numeri. I dati statistici dimostravano che la percentuale degli imputati di un qualche reato condannati con la maggioranza dei voti prescritta all'epoca, nonché il loro numero assoluto, restavano costanti nel corso degli anni. Poisson formulò allora l'ipotesi che le 'cause' di questa relativa costanza fossero valori stabili della probabilità k di colpevolezza di un imputato e della probabilità u di un giurato di pervenire a un giudizio corretto. Partendo da questi assunti, Poisson determinò la probabilità Ri che un imputato scelto 'a caso' venisse condannato con una maggioranza di almeno n−i (i⟨n/2) giurati, come funzione di k e u. Come valore di Ri Poisson assunse il rapporto m/μ, dove m indica il numero dei condannati e μ il numero complessivo degli imputati in Francia in un arco di tempo di parecchi anni. Assumendo che Ri sia costante, la probabilità che vi sia una differenza significativa tra le frequenze relative delle condanne in due intervalli di tempo diversi risulterebbe molto piccola.
I primi test semplici di significatività
Poisson sottopose entrambi i casi presi in esame a un test di significatività, definendo per ciascuno un livello di significatività e la relativa regione critica. Egli non vedeva alcuna ragione per rifiutare l'ipotesi di un Ri costante, se per questa ipotesi risultava una probabilità P di una differenza tra le due frequenze relative m/μ e m′/μ′ pari al massimo a β, che a sua volta raggiungeva perlomeno il valore 1−α; dunque:
Nella [17] α, che caratterizza il livello di significatività, e β, che definisce la regione critica ‒ ossia l'insieme dei valori Ri per i quali la differenza a primo membro risulta maggiore di β ‒ sono numeri positivi relativamente piccoli. Essi sono a loro volta reciprocamente dipendenti dimodoché, per esempio, un valore minore di β porta a un valore maggiore di α e viceversa.
Poiché tale differenza cambiava in misura significativa da un anno all'altro, era lecito dedurne un mutamento del sottostante sistema di cause.
Il tipo di test di significatività adottato qui da Poisson era stato già prefigurato da Laplace. Anche nella teoria degli errori, del resto, si utilizzavano test elementari, non al fine di scartare o di accettare un'ipotesi sulla base di dati empirici, bensì per eliminare particolari dati che si discostavano eccessivamente da una distribuzione teorica.
I semplici test di significatività utilizzati al di fuori della teoria degli errori si basavano quasi sempre, come accade in Poisson, sulla valutazione della significatività di due ipotesi: i risultati del campione possono essere casuali, oppure riconducibili a un sistema di cause. Laplace, per esempio, in un lavoro del 1823 sull'influenza della Luna sull'atmosfera, aveva affermato in via generale che accanto all'opportuna combinazione del maggior numero possibile di osservazioni, si rendeva necessario definire un metodo per determinare la probabilità che gli errori fossero compresi entro determinati limiti; in caso contrario si correva il rischio, come accadeva troppo spesso in meteorologia, di interpretare come leggi della Natura gli effetti di fattori casuali. Già nella prima edizione della Théorie analytique des probabilités (1812) Laplace aveva proposto un metodo per evitare tali interpretazioni erronee. Da numerose osservazioni era risultato che le letture del barometro effettuate alle nove del mattino davano risultati diversi da quelle effettuate alle ore sedici. Partendo dall'ipotesi che tali discrepanze fossero casuali, Laplace cercò di adattare le differenze osservate a una adeguata distribuzione normale e ne determinò la varianza. Poiché risultò che i valori osservati si discostavano dalla loro media di una misura sette volte superiore alla varianza, Laplace rigettò tale ipotesi.
Test di significatività di questo tipo venivano utilizzati da numerosi studiosi del XIX sec. e furono ufficialmente codificati allorché vennero accolti nell'articolo Methods of statistics, di Francis Ysidro Edgeworth (1845-1926) pubblicato nel 1885 nel volume in onore del cinquantenario della Royal Statistical Society. Edgeworth fu uno dei primi autori, nell'ambito della scuola biometrica fondata da Francis Galton, a sottolineare le differenze tra la teoria degli errori del calcolo delle probabilità e un nuovo tipo di statistica, dando così avvio al processo di emancipazione della statistica matematica dal calcolo delle probabilità. Fra tali differenze, accolte successivamente da Galton e più tardi da Karl Pearson (1857-1936) vi è quella tra osservazioni e statistica. Mentre la media di una serie di misurazioni serve a determinare una grandezza media reale (come una lunghezza oppure un intervallo di tempo), la media statistica di una serie di dati relativi a una caratteristica di una popolazione è qualcosa di fittizio, poiché a essa non corrisponde alcun valore reale. Concetti statistici come quello di altezza media o di propensione media al crimine dell'homme moyen, figura introdotta da Quételet, non hanno alcun riscontro reale in un individuo, ma servono a descrivere una data caratteristica in una popolazione.
In Methods of statistics Edgeworth propose un test di significatività per stabilire se la differenza tra due valori medi fosse da considerarsi o meno casuale. Edgeworth definisce 'dispersione' la quantità c uguale all'oscillazione delle medie di due serie di misurazioni. Nel caso della media aritmetica
e la dispersione c possono anche determinarsi in altro modo, per esempio attraverso il calcolo della mediana e della densità della popolazione. Una volta calcolati con la [18] i quadrati delle dispersioni c21 e c22 relativi alle medie
risulta maggiore di 2c, l'ipotesi che si tratti di una differenza casuale viene rifiutata come altamente improbabile (il che corrisponde a un livello di significatività di circa 0,005).
Sebbene il ruolo di Edgeworth negli sviluppi successivi della statistica sia considerato marginale, la sua corrispondenza con Pearson negli anni Novanta dell'Ottocento dimostra come egli abbia esercitato un'influenza notevole sullo stesso Pearson, che avrebbe segnato con la sua impronta i contenuti e gli indirizzi della statistica matematica. In una serie di contributi del 1893, per esempio, Pearson si rifà in misura notevole al test di significatività di Edgeworth, anche se sostituisce al concetto di modulo quello oggi corrente di deviazione standard. I test di significatività sono stati ampliati e applicati sistematicamente solo nel XX sec. e l'inizio di questo sviluppo può essere considerato il test di adattamento o del χ2 elaborato da Pearson nel 1900, attraverso il quale si misura la bontà di adattamento di una distribuzione teorica a una distribuzione empirica.
L'aritmetica politica inglese fu fondata nella seconda metà del XVII sec. da John Graunt (1620-1674) e da John Petty (1623-1687). Si diffuse in Germania nel secolo successivo ‒ nel contesto del pietismo e degli sforzi tesi a dimostrare l'esistenza e l'azione di Dio attraverso l'ordine naturale ‒ soprattutto a opera di Peter Süssmilch (1707-1767) e del suo scritto Göttliche Ordnung in der Veränderungen des menschlichen Geschlechts (L'ordine divino nelle trasformazioni del genere umano). Scopo dell'aritmetica politica era quello di fornire al responsabile o ai responsabili delle decisioni nello Stato le informazioni sulle risorse umane ed economiche del paese attraverso una serie di dati, per esempio sulle condizioni o sull'età della popolazione.
Con l'astronomo e matematico belga Lambert-Adolphe-Jacques Quételet l'aritmetica politica si trasformò in una fisica sociale, quale era stata già propugnata da Auguste Comte (1798-1857). Nato nel 1796, alla fine del 1823 Quételet compì un viaggio di studio di alcuni mesi in Francia a spese del governo belga, soprattutto per acquisire le cognizioni astronomiche necessarie per realizzare l'osservatorio di Bruxelles, all'epoca in costruzione. In Francia Quételet entrò in contatto con Jean-Baptiste-Joseph Fourier e con Pierre-Simon de Laplace, di cui studiò la teoria della probabilità. Nel 1826 divenne socio corrispondente dell'Ufficio di statistica belga. Incaricato di effettuare il censimento degli abitanti del regno del Belgio, nato nel 1830 a seguito della scissione dall'Olanda, Quételet utilizzò dapprima quelli che allora venivano chiamati metodi laplaciani per la stima della popolazione. Data la relativa inattendibilità dei registri delle nascite e delle morti e le difficoltà di attuare un censimento demografico completo, Laplace aveva proposto di dedurre tale stima dal tasso medio di natalità, calcolato sul numero di nati in un anno, o dal tasso medio di mortalità calcolato sul numero dei decessi, effettuando una media dei tassi annuali di natalità o di mortalità determinati con grande accuratezza nell'arco di alcuni anni in una serie di distretti. Il problema di selezionare un campione rappresentativo di tali distretti per compensare le palesi disomogeneità dei tassi di natalità e di mortalità presentava ancora all'epoca difficoltà insormontabili. I valori trovati per la popolazione complessiva, per esempio, differivano notevolmente a seconda dei distretti scelti, o a seconda che si partisse dai dati sulla mortalità o da quelli sulla natalità.
La disomogeneità dei dati così ottenuti, indusse Quételet ad abbandonare i metodi di Laplace e a optare per un censimento completo della popolazione, senza dubbio assai più dispendioso ma più attendibile. In Quételet, dunque, non è dato trovare nessun accenno a uno sviluppo della teoria dei campioni. Come la maggior parte dei pionieri della statistica, Quételet era quasi ossessionato dall'idea che contando, ponderando, misurando e confrontando i dati relativi a determinate caratteristiche, opportunamente riportati in grafici o tabelle, sarebbe stato possibile stabilire relazioni tra tali elementi. Egli analizzava per esempio i tassi di natalità e di mortalità conformemente alla stagione, alla località, alla temperatura o all'ora del giorno.
Quételet si interessò alla mortalità in diverse professioni e zone climatiche, nelle carceri o negli ospedali. Inoltre raccolse dati su altezza, peso, tassi di crescita e forza del corpo umano, nonché sulla quota di alcolizzati, di minorati mentali, di suicidi e di criminali nella popolazione complessiva. I dati raccolti sino ad allora e in parte già pubblicati vennero riepilogati nello scritto Sur l'homme et le développement des ses facultés, ou Essai de physique sociale, apparso nel 1835.
Quest'opera, e il nuovo concetto di uomo medio che Quételet vi sviluppava, gli guadagnarono ben presto notorietà in tutta Europa. Il vivo interesse suscitato da questo autore viene ricollegato di solito a un atteggiamento egualitario che rispondeva alle aspettative della borghesia europea dell'Ottocento. Tuttavia una ragione di questo successo, perlomeno altrettanto importante dello studio di caratteristiche che riguardavano allo stesso modo nobili e borghesi, contadini e operai, è la loro riduzione a numero e misura. La quantificazione rispondeva all'esigenza della borghesia che cariche e uffici nell'apparato statale e nell'esercito fossero assegnati unicamente in base al principio dell'efficienza. Particolarmente impressionanti, e quindi argomento di discussione nell'alta società europea, erano i dati relativi alla propensione a delinquere. Sulla base dei dati riportati nelle statistiche criminali pubblicate in Francia tra il 1825 e il 1830, Quételet cercò di stabilire se le differenze tra il tasso di condanne (inteso come rapporto tra il numero dei condannati e il numero complessivo degli imputati) in determinate categorie della popolazione, per esempio negli individui con un grado elevato di istruzione, e il tasso generale di condanne fossero significative oppure casuali. Qui Quételet mostra una qualche consapevolezza dei problemi affrontati dall'attuale analisi della varianza, ma nulla più, poiché gli mancavano gli strumenti sia concettuali sia matematici per risolvere problemi di questo genere.
L'homme moyen di Quételet rappresentava il valore medio di una caratteristica distribuita su tutta la popolazione o su un campione opportunamente scelto, come per esempio l'altezza media delle reclute francesi, che si poteva confrontare con altre stature medie, come quella della popolazione maschile in Francia o quella delle reclute di altri paesi. Questo esempio dimostra che Quételet non considerava l'uomo medio tout court, bensì vari uomini medi a seconda dei gruppi d'età, delle razze, delle nazioni e così via. Attraverso l'homme moyen così concepito egli poteva eliminare le variazioni casuali nei fenomeni sociali, evidenziando invece quelle regolarità che costituivano le 'leggi' della sua 'fisica sociale' modellata sulla meccanica newtoniana. Come variazioni casuali andavano considerati per esempio gli scarti rispetto al valore medio riscontrati nei singoli individui relativamente alla presenza di una caratteristica. Tali oscillazioni verso l'alto o verso il basso erano equiparate da Quételet agli errori casuali nelle misurazioni. Alla sua concezione, improntata all'immagine negativa dell'errore, faceva riscontro una valutazione positiva del valore medio, ovvero dell'uomo medio come tipo ideale cui tende la Natura. Quételet si serviva a questo riguardo della similitudine del tiratore che prende di mira un bersaglio circolare: il circoletto nero al centro del bersaglio rappresenta il fine cui tende la Natura e i fori dei colpi via via più radi che cadono all'esterno di tale centro rappresentano gli individui che si discostano in misura maggiore o minore dall'ideale dell'uomo medio.
Questa similitudine suggerisce anche che la distribuzione degli scarti dalla media, qualora non intervengano fattori di disturbo, corrisponde sempre alla distribuzione di un egual numero di colpi messi a segno nel bersaglio. Poiché la distribuzione di frequenza delle distanze dei tiri dal centro del bersaglio all'aumentare del numero dei tiri tende a descrivere una curva, che corrisponde al ramo destro, positivo, di una distribuzione normale, Quételet affermava che anche la distribuzione degli scarti dalla media di un caratteristica, qualora non intervengano cause particolari, converge alla distribuzione normale. Alla dimostrazione che una distribuzione empirica degli scarti dalla media di una caratteristica tende alla distribuzione normale, Quételet associava l'interpretazione di tali scarti come effetti di "cause puramente accidentali", ossia come variazioni casuali della media della popolazione. Alla base di tale interpretazione vi era l'ipotesi degli errori elementari, secondo cui la distribuzione di errori casuali, a loro volta intesi come somma di una pluralità di errori elementari indipendenti dello stesso ordine di grandezza, è approssimativamente normale.
Viceversa, dall'impossibilità di fornire una tale dimostrazione Quételet deduceva l'intervento di altri fattori non casuali.
Per dimostrare che scarti dalla media di una caratteristica nella popolazione hanno una distribuzione prossima alla normale, Quételet cercò di adattare la distribuzione di frequenza degli scarti riscontrata empiricamente a una distribuzione binomiale simmetrica. La distribuzione binomiale scelta corrispondeva all'esito di 999 estrazioni da un'urna contenente sempre lo stesso ugual numero di pietre nere e bianche. Pertanto Quételet aveva calcolato e rappresentato in un istogramma la probabilità
di aver estratto alla 999-esima estrazione ν volte una pietra bianca e (999−ν) volte una pietra nera.
Tale distribuzione corrispondeva quindi a n=999 e p=q=1/2. Quételet illustrò i singoli passi del metodo elementare di adattamento da lui adottato nelle Lettres à S.A.R. le duc régnant de Saxe-Cobourg et Gotha, sur la théorie des probabilités, appliquée aux sciences morales et politiques, apparse nel 1846, servendosi di esempi come la distribuzione delle misure toraciche di 5738 soldati scozzesi.
Come misura della bontà dell'adattamento della distribuzione empirica delle misure toraciche dei soldati scozzesi a questa distribuzione binomiale simmetrica, Quételet giudicò sufficienti le differenze relativamente piccole tra i numeri dei soldati che rispondevano alle varie misure toraciche nelle due distribuzioni. Nello stesso tempo egli si richiamò al piccolo intervallo intorno all'ampiezza toracica media, stabilito con un errore probabile di circa 33 mm, in cui rientravano, nei due casi, le misure di metà dei 5738 soldati. L'errore probabile, secondo Quételet, non sarebbe risultato minore misurando 5738 volte l'ampiezza toracica di un singolo soldato scozzese. Osservando la distribuzione delle misure toraciche dei 5378 soldati scozzesi, concludeva Quételet, si ricavava l'impressione che la Natura avesse cercato di riprodurre 5738 volte il tipo ideale approssimato dalle misure toraciche medie, incorrendo in corrispondenti errori casuali.
Le disomogeneità riscontrate già in precedenza nei tassi di natalità e di mortalità in Belgio, che indussero Quételet a pronunciarsi per un censimento demografico completo, non gli impedirono di postulare l'omogeneità delle popolazioni da lui esaminate in relazione a una data caratteristica. Egli riteneva che tale ipotesi fosse giustificata dalla bontà dell'adattamento delle distribuzioni empiriche a distribuzioni binomiali simmetriche prossime alla normale.
Quételet studiò anche l'adattamento di distribuzioni empiriche non uniformi, per esempio relative a dati meteorologici, a distribuzioni binomiali asimmetriche, e riconobbe l'esistenza di altre distribuzioni empiriche asimmetriche; tuttavia egli apparve agli occhi della maggioranza dei contemporanei come un sostenitore del predominio della distribuzione normale in Natura. Assumendo una corrispondenza tra omogeneità e distribuzione normale, Quételet era ancora ben lontano dall'idea che fosse possibile una distribuzione non normale di dati omogenei, oppure una distribuzione normale di dati non omogenei. Egli non riuscì quindi a trovare una soluzione soddisfacente al problema di analizzare le dispersioni nei dati empirici. La centralità attribuita all'uomo medio lo induceva a concentrare l'attenzione sulle regolarità vere o presunte presentate dai dati sociali, sulla potente e auspicata stabilità della società, trascurando le oscillazioni e le variazioni.
Tra gli autori della generazione successiva, tra i quali spicca la figura dell'economista e matematico Wilhelm Lexis (1837-1914), le leggi della fisica sociale postulate da Quételet suscitarono reazioni diverse. I critici ritenevano che tali leggi rappresentassero una pesante limitazione, se non una negazione della responsabilità umana e del libero arbitrio. Furono queste considerazioni, accanto a motivi di natura politica, a indurre Lexis a dedicarsi all'analisi della variazione di serie di osservazioni condotte in successivi periodi di tempo, note oggi come serie storiche o temporali. Nel 1879 egli introdusse il cosiddetto coefficiente di dispersione Q, che misura il rapporto tra la dispersione R osservata nei dati empirici e la dispersione r in una distribuzione binomiale adattata ai dati. Se Q risulta maggiore di 1 le oscillazioni nei valori della serie non possono essere rappresentate in base al modello dell'urna corrispondente alla distribuzione binomiale; la serie non è stabile e le oscillazioni vanno ricondotte all'azione di fattori legati al tempo. Se il valore di Q risulta uguale o prossimo a 1, si tratta di una serie stabile nel tempo alla quale può essere applicato il modello binomiale. Se infine Q è minore di 1, la dispersione nella serie è minore di quella ammessa dal modello dell'urna. Una tale stabilità 'sovranormale' potrebbe essere frutto, per esempio, dell'azione prolungata nel tempo di norme legislative che impongono determinate quote.
Il caso di Q uguale o prossimo a 1 ‒ il criterio di Lexis per una serie 'stabile' ‒ risultava però eccessivamente selettivo sul piano pratico, poiché escludeva, in quanto non sufficientemente stabili, numerose serie di dati di rilevanza sociale. L'esiguo numero di serie storiche stabili, come ad esempio il rapporto tra i sessi nelle nascite, appariva già ai contemporanei frutto di leggi non sociali, bensì biologiche. Inoltre, Q poteva assumere un valore così prossimo a 1 che la differenza stessa poteva essere interpretata come frutto del caso. Ancora, un valore di Q relativamente molto vicino a 1 (come 1,1) in base alla formula di approssimazione data da Lexis per popolazioni molto grandi
Sulle orme di Lexis il suo allievo Ladislaus von Bortkiewicz (1868-1931), studiando eventi rari, per esempio i dati relativi al numero di soldati dell'esercito prussiano morti a seguito di un calcio di un cavallo, trovò nel 1898 che essi, sebbene presentassero oscillazioni annuali relativamente consistenti e fossero quindi instabili, a causa del valore di p che risultava molto piccolo soddisfacevano il criterio di stabilità di un coefficiente di dispersione prossimo a 1.
Oltre che da Bortkiewicz, le ricerche di Lexis sono state proseguite nel XX sec. soprattutto dai due matematici russi Markov e Aleksandr Aleksandrovič Čuprov (1874-1926), i cui contributi all'analisi della varianza peraltro non hanno avuto un'importanza paragonabile a quella dei metodi sviluppati nell'ambito della scuola biometrica inglese.
Regressione e correlazione, i due concetti chiave della nuova statistica matematica
Il fondatore della scuola biometrica inglese fu Francis Galton (1822-1911). Entrato in possesso della sua eredità, egli decise di abbandonare gli studi di medicina per dedicarsi interamente ai suoi molteplici interessi scientifici. Dopo una serie di viaggi che lo portarono a compiere una lunga esplorazione in Africa e a occuparsi di meteorologia, verso la metà degli anni Sessanta dell'Ottocento la sua attenzione si focalizzò sullo studio dell'ereditarietà e in particolare dell'ereditarietà umana. A spingere Galton in questa direzione contribuirono sia i suoi interessi per i problemi sociali, sia l'influenza della teoria della selezione formulata dallo zio Charles Darwin. Egli si propose di quantificare gli effetti dell'evoluzione guidata dalla selezione, nella convinzione che ciò avrebbe reso possibile influenzare l'evoluzione umana attraverso misure 'eugenetiche'. Il primo frutto dei suoi sforzi in questo campo è lo scritto Hereditary genius, apparso nel 1869, in cui Galton, analizzando le prestazioni intellettuali dei membri della stessa famiglia nell'arco di varie generazioni, cerca di dimostrare che le abilità eccezionali nel campo dell'arte, della scienza, della politica o dello sport sono dovute all'eredità biologica. Rifacendosi a Quételet, Galton utilizza qui la distribuzione normale per descrivere la variazione nell'ereditarietà umana.
Conscio del fatto che i dati da lui raccolti sull'ereditarietà in famiglie di scienziati d'eccezione non consentivano una sistematizzazione matematica, Galton si dedicò agli esperimenti di selezione, passando allo studio dell'ereditarietà del peso nei piselli. A tal fine egli divise una certa quantità di semi di piselli, il cui peso aveva una distribuzione prossima alla normale con valore medio M e dispersione c1, in sette gruppi di dimensioni eguali nei quali il peso medio assumeva i seguenti valori
e li coltivò separatamente ma in condizioni identiche. Nei piselli della generazione successiva la distribuzione del peso in ogni gruppo risultava nuovamente vicina alla normale, con la stessa dispersione f, ossia lo stesso grado di variabilità espresso da Galton attraverso la valutazione dell'errore probabile. Anche nella totalità dei piselli di questa generazione la distribuzione del peso era prossima alla normale, con la stessa dispersione c2 intorno a M. Se i valori medi dei singoli gruppi fossero rimasti eguali nella generazione dei genitori e nella generazione F1, era lecito aspettarsi, in contrasto con i risultati empirici, un aumento della dispersione complessiva di generazione in generazione, che avrebbe ben presto compromesso la costanza della specie. Invece risultava che i valori medi nei singoli gruppi della generazione F1 non erano eguali a quelli riscontrati nella generazione dei genitori. I valori medi della generazione F1 evidenziavano uno slittamento lineare verso la media globale M, vale a dire, la dispersione nei singoli gruppi di tale generazione si attestava intorno ai sette valori medi
A causa del fenomeno che Galton definisce 'reversione', nella generazione F1 gli scarti dei valori medi dei singoli gruppi dal valore medio M si erano ridotti del fattore r rispetto alla generazione dei genitori.
Dal fatto che a partire da piselli della generazione dei genitori, di peso M+x, si pervenga a piselli della generazione F1, di peso M+z, si è indotti a concludere che la variazione z rispetto al peso medio globale M consiste di due componenti: la prima (r1x) è dovuta alla reversione r1 dalla generazione dei genitori, la seconda (r2y) alla reversione r2 relativa alle variazioni di peso nei diversi gruppi della generazione F1.
Dato che le dispersioni complessive c1=σ(x) e c2=σ(z) sono uguali (come stabilito da Galton), indicato con c il loro comune valore e posto f=σ(y), risulta:
Quest'ultima relazione era stata dedotta dalla reversione osservata empiricamente, ma non realmente giustificata. Solo nel 1885 Galton fu in grado di offrire una spiegazione in merito, in un'epoca in cui aveva trasposto il fenomeno della reversione all'ambito umano ribattezzandola 'regressione'.
In quell'anno, come presidente della British Association of the Advancement of Science, Galton presentò i risultati di una importante ricerca in cui l'altezza di 930 individui adulti veniva messa a confronto con quella dei loro 'genitori medi'. L'altezza dei genitori medi era calcolata come valore medio tra l'altezza del padre e quella della madre (quest'ultima moltiplicata per 1,08, fattore che rappresenta il rapporto tra l'altezza media degli uomini e quella delle donne). Introducendo il genitore medio, Galton si proponeva di creare una situazione analoga a quella dell'esperimento precedente, in cui a causa dell'autofecondazione era stato preso in considerazione un solo genitore. Galton escludeva in via preliminare che fattori come, per esempio, la predilezione di uomini e donne per partners alti o bassi, oppure che grandi differenze di altezza dei genitori di contro a piccole differenze nel valore medio, potessero influire in modo significativo sul genitore medio. Galton costruì poi una tabella dove nelle righe si aveva la distribuzione delldei figli per valori costanti del genitore medio e nelle colonne la distribuzione dei genitori per valori costanti dei figli. Egli determinò inoltre la posizione di tutti i punti (x,y) in un sistema di coordinate, dove x indica l'altezza dei figli e y quella dei genitori medi, in cui il numero n di figli ha di volta in volta lo stesso valore. Galton trovò che i punti per un valore n costante giacciono su un'ellisse e che valori diversi di n danno analoghe ellissi concentriche con lo stesso orientamento dell'asse principale. Congiungendo i punti di contatto di una tangente orizzontale a due di tali ellissi si ottiene una retta inclinata verso la verticale, che corrisponde alla regressione dal genitore medio ai figli, mentre congiungendo i punti di contatto di una tangente verticale si ottiene una retta inclinata verso l'orizzontale, corrispondente alla regressione dai figli al genitore medio.
Galton concluse che una retta orizzontale corrisponde a un valore fisso del genitore medio, che nel punto di contatto di un'ellisse raggiunge il massimo della relativa funzione (vincolata) di distribuzione. Quest'ultima interpretazione fu formulata da Galton con l'ausilio del matematico J. Hamilton Dickson, il quale gli aveva chiarito che le ellissi da lui trovate empiricamente rappresentano le curve di frequenza costante in una distribuzione normale bidimensionale.
La scoperta di una simmetria statistica della regressione condusse infine Galton a formulare l'ipotesi che la regressione non è che un caso speciale di una relazione statistica più generale tra due caratteristiche, ossia della correlazione.
Francis Galton giunse a tale ipotesi analizzando la relazione tra due caratteristiche, quali l'altezza e la lunghezza dell'avambraccio in una stessa popolazione. Lo studioso si era posto il problema della dipendenza o indipendenza reciproca di caratteristiche fisiche diverse in connessione con il metodo messo a punto dall'antropologo e criminologo francese Alphonse Bertillon (1853-1914) per identificare gli individui, e nella fattispecie i criminali, attraverso le misure di varie parti del corpo. Essenziale per il funzionamento del sistema di Bertillon era l'asserita indipendenza delle misure utilizzate. Galton riuscì a stabilire l'esistenza di una regressione dall'altezza alla lunghezza del braccio e dalla lunghezza del braccio all'altezza, che corrispondeva a quella dall'altezza dei figli all'altezza media dei genitori. Ma se la lunghezza media del braccio in individui di altezza x è pari a r1x, e l'altezza media di individui il cui braccio ha lunghezza y è pari a r2y, allora le regressioni r1 e r2 sono diverse, come egli aveva scoperto empiricamente, senza soddisfare una relazione elementare come r1r2=1. Egli scoprì però che i due valori per le regressioni r1 e r2 si riducono a un unico valore se le altezze vengono date in multipli dell'errore probabile della relativa distribuzione, e analogamente le lunghezze del braccio in multipli dell'errore probabile della distribuzione di frequenza di tali lunghezze. Questo valore r, indipendente dall'altezza e dalla lunghezza del braccio dei singoli individui, venne definito da Galton come correlazione tra le due grandezze r1 e r2.
I risultati complessivi delle ricerche di Galton sulla regressione e sulla correlazione, nonché su altri metodi da lui sviluppati per la determinazione statistica dei fattori ereditari, vennero riepilogati nello scritto Natural inheritance (1889) che divenne una sorta di Bibbia per i membri della scuola biometrica da lui fondata.
Uno dei primi e più attenti lettori di Natural inheritance fu Karl Pearson, dal 1844 professore di matematica applicata e di meccanica allo University College di Londra. Pearson si interessò subito alla misura di correlazione introdotta da Galton, interpretando la correlazione come una nuova categoria generale per indicare le interdipendenze tra grandezze, che avrebbe consentito una matematizzazione di gran parte della psicologia, della medicina e della sociologia e che aveva come unico limite la casualità. Pearson si interessò in seguito quasi esclusivamente alla rappresentazione matematica dei problemi affrontati da Galton e da Walter F.R. Weldon (1860-1906), suo collega dello University College. In competizione soprattutto con Edgeworth, Pearson creò i fondamenti di quella disciplina che già nel 1863 il tedesco Theodor Wittstein (1816-1894), in un articolo sulla statistica demografica, aveva denominato 'statistica matematica'.
Pearson rese noti i primi risultati delle sue ricerche negli anni Novanta dell'Ottocento in una serie di lezioni al Gresham College e allo University College. Solo una piccola parte dei risultati elaborati per tali lezioni fu pubblicata in quegli stessi anni. Tra essi vi è la dimostrazione matematica della riduzione dei due valori r1 e r2 a un unico valore r per la correlazione, scoperta per via empirica da Galton, e la rappresentazione analitica di r per due grandezze che soddisfano una distribuzione normale bidimensionale. Pearson, il più influente dei matematici che collaborarono con Galton, presentò una prima formulazione della teoria della correlazione in un lavoro del 1896 sull'evoluzione della specie. Qui egli determinò il 'valore migliore' di quello che Edgeworth aveva definito coefficiente di correlazione r di una distribuzione normale bidimensionale, e precisamente
Nella [24] si sommano i valori delle grandezze x e y rilevati su N individui, sottraendo alle misure empiriche x′i, y′i (i=1,…,n) il valore medio corrispondente, cioè (∑x′i)/N o, rispettivamente, (∑y′i)/N. In base a questa convenzione, sostituendo N con N−1, sx e sy sono identici alla cosiddetta dispersione empirica . Nel suo scritto del 1896 Pearson fornì anche i coefficienti di correlazione ϱij di due grandezze nel caso tridimensionale e nel caso p-dimensionale (p≥2), assumendo che la distribuzione della caratteristica considerata sia una distribuzione normale p-dimensionale. I p(p−1)/2 coefficienti ϱij definiscono interamente il grado di dipendenza tra le caratteristiche della popolazione. Due caratteristiche xi e yj sono indipendenti se e solo se ϱij=0, e linearmente dipendenti se e solo se ∣ϱij∣=1. Pearson si rendeva conto che queste relazioni non si potevano applicare al caso di distribuzioni multidimensionali irregolari, e in un lavoro del 1905 si occupò della correlazione in distribuzioni asimmetriche.
A stimolare l'interesse di Pearson per le distribuzioni irregolari fu Weldon che, nell'ambito delle sue ricerche statistiche, basate sui metodi galtoniani e relative alla variazione e alla correlazione in diverse popolazioni di piante e animali, si era imbattuto ben presto in una serie di distribuzioni asimmetriche. Tra il 1894 e il 1916 Pearson pubblicò tre lavori in cui presentava 12 tipi di densità di distribuzione y(x), che sono tutti soluzioni della medesima equazione differenziale
Pearson, che si era imbattuto in questa equazione considerando le inclinazioni dei singoli segmenti che approssimavano un poligono aventi distribuzioni binomiali e ipergeometriche simmetriche o asimmetriche, aveva sviluppato i dodici diversi tipi di densità di distribuzione differenziabile per l'adattamento a una varietà di distribuzioni di frequenza empiriche. Come test per la bontà dell'adattamento ai suoi tipi teorici Pearson sviluppò nel 1900 il test del χ2. I risultati di Pearson hanno avuto tra i biologi e i sociologi una straordinaria risonanza, che ha contribuito in misura decisiva all'abbandono del dogma, affermatosi con Quételet, del predominio della distribuzione normale nella spiegazione di tutti i fenomeni di variazione in campo biologico, fisico e sociale.
Bibliografia
Daston 1988: Daston, Lorraine, Classical probability in the enlightenment, Princeton, Princeton University Press, 1988.
Eisenhart 1974: Eisenhart, Churchill, Pearson, Karl, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. X, 1974, pp. 447-473.
Fischer 2000: Fischer, Hans, Die verschiedenen Formen und Funktionen des zentralen Grenzwertsatzes in der Entwicklung von der klassischen zur modernen Wahrscheinlichkeitsrechnung, Aachen, Shaker, 2000.
Gigerenzer 1989: Gigerenzer, Gerd [et al.], The empire of chance. How probability changed science and everyday life, Cambridge, Cambridge University Press, 1989.
Gillispie 1997: Gillispie, Charles Coulston, Pierre Simon Laplace (1749-1827). A life in exact science, with the collaboration of Robert Fox and Ivor Grattan-Guinness, Princeton, Princeton University Press, 1997.
Hacking 1990: Hacking, Ian, The taming of chance, Cambridge, Cambridge University Press, 1990.
Hald 1998: Hald, Anders, A history of mathematical statistics from 1750 to 1930, New York, Wiley, 1998.
Heyde 1977: Heyde, Christopher C. - Seneta, Eugene, I.J. Bienaymé. Statistical theory anticipated, New York, Springer, 1977.
MacKenzie 1981: MacKenzie, Donald A., Statistics in Britain, 1865-1930. The social costruction of scientific knowledge, Edinburgh, Edinburgh University Press, 1981.
Maistrov 1974: Maistrov, Leonid E., Probability theory. A historical sketch, translated and edited by Samuel Kotz, New York-London, Academic Press, 1974.
Pearson 1970-77: Studies in the history of statistics and probability, a series of papers selected and edited by Egon S. Pearson and Maurice G. Kendall, London, Griffin, 1970-1977, 2 v.
Pearson 1914-30: Pearson, Karl, The life, letters and labours of Francis Galton, Cambridge, Cambridge University Press, 1914-1930, 3 v. in 4 tomi; v. I: Birth, 1822 to marriage, 1853, 1914; v. II: Researches of middle life, 1924; v. III A, Correlation, personal identification and eugenics, 1930; v. III B, Characterisation, especially by letters. Index, 1930.
Porter 1986: Porter, Theodore M., The rise of statistical thinking, 1820-1900, Princeton, Princeton University Press, 1986.
Schneider 1975: Schneider, Ivo, Rudolph Clausius' Beitrag zur Einführung wahrscheinlichkeitstheoretischer Methoden in die Physik der Gase nach 1856, "Archive for history of exact sciences", 14, 1975, pp. 237-261.
‒ 1987: Schneider, Ivo, Laplace and thereafter. The status of probability calculus in the nineteenth century, in: The probabilistic revolution, edited by Lorenz Krüger, Cambridge (Mass.), MIT Press, 1987, 2 v.; v. I: Ideas in history, edited by Lorenz Krüger, Lorraine J. Daston and Michael Heidelberger, pp. 191-214.
‒ 1988: Schneider, Ivo, Die Entwicklung der Wahrscheinlichkeitstheorie von den Anfängen bis 1933. Einführungen und Texte, Darmstadt, Wissenschaftliche Buchgesellschaft, 1988.
‒ 1990: Schneider, Ivo, Gauss' contributions to probability theory, in: Symposia Gaussiana. Series A. Mathematics and theoretical physics, edited by M. Behara, I, Berlin-Toronto-Sâo Paulo, Institutum Gaussianum, 1990, pp. 72-84.
Stigler 1986: Stigler, Stephen M., The history of statistics. The measurement of uncertainty before 1900, Cambridge (Mass.)-London, Harvard University Press, 1986.