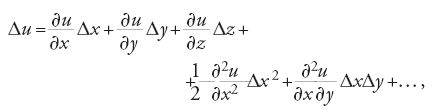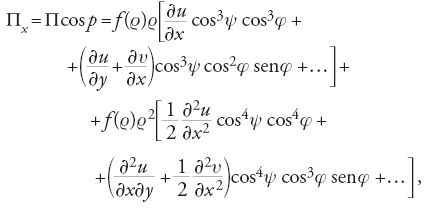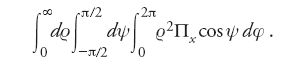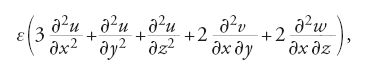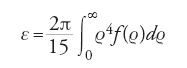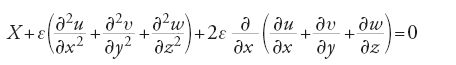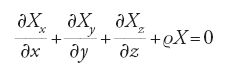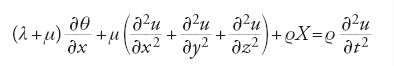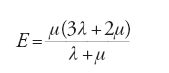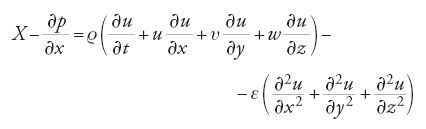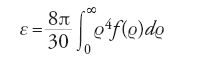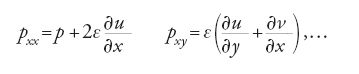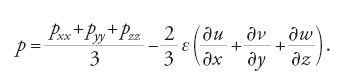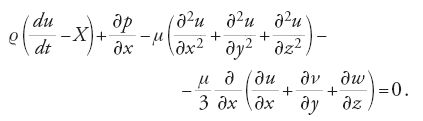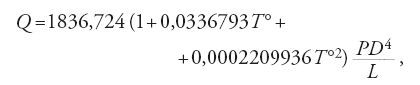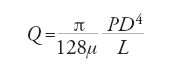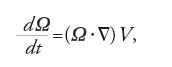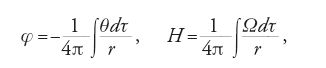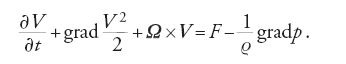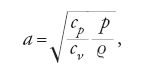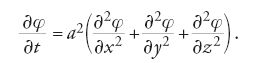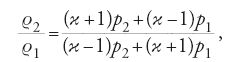L'Ottocento: matematica. Elasticità e idrodinamica

L'Ottocento: matematica. Elasticita e idrodinamica

Elasticità e idrodinamica

Il XIX sec. rappresenta per la storia della meccanica dei continui un periodo particolarmente importante, i cui progressi sono caratterizzati dallo sviluppo di idee generali e dalle prime serie applicazioni pratiche. Queste ultime erano strettamente connesse con la rapida crescita della produzione capitalistica, in particolar modo con l'espansione delle ferrovie e dell'ingegneria strutturale, che rappresentava un'impellente motivazione per lo studio della resistenza delle costruzioni e dei calcoli per la loro progettazione.

I maggiori progressi in questo settore si ebbero quindi grazie alla precedenza di cui godeva lo sviluppo della meccanica dei solidi deformabili. Furono infatti eseguiti esperimenti sulla resistenza dei materiali e delle costruzioni, venne perfezionata una teoria dei materiali ponendo in questo modo le basi della teoria dell'elasticità, che permise tanto di prendere in esame quanto di raffinare un'analisi ingegneristica più semplice.

Il caso della dinamica dei fluidi fu, per vari motivi, diverso. All'inizio del XIX sec. la pratica ingegneristica aveva accumulato un gran numero di dati relativi all'idraulica delle tubazioni e dei fiumi e al moto dei corpi in acqua. Tuttavia la teoria matematica non fu in grado di offrire risposte alla questione fondamentale, che riguardava sia l'origine della resistenza idrodinamica, sia il modello matematico che potesse descriverla. Nella dinamica generale dei fluidi furono ottenuti molti eleganti risultati teorici, praticamente però privi di applicazioni ingegneristiche (con l'unica eccezione parziale della teoria delle maree). L'integrazione dell'ingegneria idraulica con la dinamica dei fluidi non fu raggiunta fino al XX secolo.

è proprio dal primo decennio del Novecento che comincia il successivo stadio della meccanica dei continui, caratterizzato soprattutto dai risultati fondamentali conseguiti in idroaerodinamica che hanno trovato ampia applicazione in aeronautica. Confrontato con i progressi della dinamica dei fluidi, lo sviluppo della meccanica dei solidi retrocede, nei primi decenni del secolo, al secondo posto.

Prima di tratteggiare l'evoluzione della meccanica dei continui nel corso del XIX sec., sembra opportuno ricordare i successi che questo ramo della scienza aveva conseguito all'inizio dell'Ottocento.

Nella meccanica dei corpi deformabili si registrano soprattutto risultati che riguardano lo studio di problemi monodimensionali (o quasi monodimensionali). Si può inoltre menzionare una teoria elementare della flessione (e torsione) elastica delle travi (Parent e Coulomb), l'analisi della vibrazione delle corde e delle travi, le forme d'equilibrio e stabilità delle travi (Daniel Bernoulli, d'Alembert, Euler, Lagrange), l'introduzione implicita del modulo d'elasticità (Euler) e alcune idee relative agli sforzi normali e di taglio (Euler, Coulomb); di natura leggermente diversa è la teoria di Coulomb della pressione terrestre. Tuttavia non è possibile rintracciare alcun approccio generale alla costruzione della meccanica dei corpi deformabili prima dei celebri lavori di Claude-Louis-Marie-Henri Navier (1785-1836) e Augustin-Louis Cauchy (1789-1857), di cui si parlerà in seguito.

Al contrario, la meccanica dei fluidi e dei gas conseguì una serie di importanti risultati di tipo generale. Fu introdotta una chiara idea di pressione in un fluido ideale (Daniel e Johann II Bernoulli, Euler), furono sviluppati alcuni aspetti dell'idraulica di un fluido ideale, inclusa l'equazione di Bernoulli (Daniel e Johann II Bernoulli, Euler), e il teorema di Borda. Infine, grazie soprattutto all'opera di Leonhard Euler (1707-1783), furono poste le basi della dinamica di un fluido ideale (incomprimibile e in parte anche nel caso comprimibile). È degno di nota il fatto che Euler abbia ricavato le equazioni generali della dinamica dei fluidi seguendo un approccio al problema dei continui piuttosto moderno. Sarebbe tuttora difficile aggiungere qualcosa ai risultati di Euler (se non per correggere, naturalmente, alcuni aspetti che riguardano la termodinamica del problema e le onde di shock). Tuttavia la teoria idrodinamica generale di un fluido ideale, sebbene di formulazione estremamente elegante, non trovò applicazioni pratiche nel corso del XVIII sec., eccetto che per l'acustica, disciplina che a quel tempo si basava sull'ipotesi di Newton di propagazione isoterma del suono. Le idee di Euler avevano apparentemente bisogno soltanto di una lieve generalizzazione ‒ la naturale introduzione del concetto di sforzo di taglio ‒ per assicurare lo sviluppo dell'intera meccanica classica dei continui. Presumibilmente, però, proprio l'aver lasciato indietro le necessità pratiche del tempo fece sì che un impulso agli ulteriori sviluppi della meccanica dei continui venisse quasi un secolo più tardi da ricerche fenomenologiche basate su modelli molecolari. Una trattazione fondata puramente sulle idee di Euler e di Cauchy sui continui fu sviluppata in modo coerente dalla scuola inglese dapprima nel corso degli anni Quaranta, ma ottenne un pieno riconoscimento solamente durante gli ultimi trent'anni del XIX secolo.

Guardando ai progressi della meccanica nel corso del XIX sec., si deve inoltre ricordare l'introduzione di alcuni concetti di termodinamica in meccanica, durante la seconda metà dell'Ottocento, introduzione che giocò un ruolo importante nella comprensione dei fondamenti e influenzò gli ulteriori sviluppi della meccanica del continuo e in particolar modo della dinamica dei gas.

Equilibrio di un corpo elastico

Gli elementi fondamentali della teoria dell'elasticità furono definiti dalla scuola francese nel corso degli anni Venti e Trenta del XIX sec., soprattutto nei lavori di Navier, Cauchy, Siméon-Denis Poisson, Gabriel Lamé, Émile Clapeyron e, successivamente, di Adhémar-Jean-Claude Barré de Saint-Venant.

Il fattore determinante nel successivo sviluppo della teoria dell'elasticità e dell'intera meccanica dei continui fu il punto di vista che Cauchy elaborò negli anni Venti, anche se un impulso al progredire della teoria dell'elasticità e dell'idrodinamica di un liquido viscoso era già stato dato da due memorie presentate da Navier all'Académie des Sciences di Parigi nel 1821 e nel 1822. In esse Navier, sulle tracce di Pierre-Simon de Laplace (1749-1827), utilizzando un modello molecolare fenomenologico di un mezzo, ottenne per la prima volta le equazioni della teoria dell'elasticità per un corpo isotropo e le equazioni di flusso per un liquido viscoso incomprimibile: le cosiddette 'equazioni di Navier-Stokes'.

Rendendo giustizia al ruolo storico dei lavori di Navier, ci si soffermerà qui più dettagliatamente sul primo: il Mémoire sur les lois de l'équilibre et du mouvement des corps solides élastiques presentato all'Académie il 14 maggio del 1821.

Navier considera un corpo elastico come costituito da un insieme di 'molecole materiali' che subiscono interazioni per effetto di forze attrattive e repulsive dovute al calore. Nello 'stato naturale' del corpo queste forze di interazione sono in equilibrio. Le deformazioni del corpo causate da forze esterne provocano lo spostamento delle molecole e la generazione di forze di interazione tra tutte le molecole; queste forze, Π(ϱ)=f(ϱ)∙Δϱ, sono proporzionali alla variazione Δϱ della distanza ϱ tra le molecole e a una funzione f(ϱ) che decresce rapidamente all'aumentare di ϱ.

Indichiamo con u, v, w, gli spostamenti di un punto M (x,y,z) del corpo paralleli agli assi delle coordinate, e con u+Δu, v+Δv, w+Δw gli spostamenti del punto M′(x+Δx, y+Δy, z+Δz). Navier sviluppa gli incrementi degli spostamenti Δu, Δv e Δw in serie della forma

e, limitandosi ai termini del secondo ordine della [1], sostituisce queste espressioni nella formula

[2] ∆ϱ=∆ucosp+∆vcosq+∆wcosr,

dove p, q, r sono gli angoli che la retta MM′ forma con gli assi delle coordinate. Egli poi calcola le componenti della forza Π lungo gli assi. Introducendo l'angolo ψ formato dalla retta MM′ con il piano xy e l'angolo φ tra la proiezione di MM′ su questo piano e l'asse x, si ottiene per la componente Π_x

dove la prima espressione è dovuta ai termini del primo ordine nelle espansioni Δu, Δv, Δw, e l'altra a quelli del secondo. Navier integra Π_x sul volume e trova la componente di tutte le forze molecolari lungo l'asse x:

Sostituendo nella [4] l'espressione [3] di Π_x; inoltre considerando che (in virtù della simmetria della posizione delle molecole nel corpo) tutti i termini che contengono le potenze dispari di cosψ, cosφ e senφ (e, in particolare, tutti i termini della prima espressione nella [3]) hanno un integrale nullo, egli ottiene alla fine, per l'integrale [4], l'espressione seguente:

dove

è una costante che descrive le caratteristiche elastiche del mezzo. Dopo aver uguagliato l'espressione ottenuta in questo modo con X, la forza di volume agente, Navier ottiene le equazioni di equilibrio richieste per un corpo elastico isotropo, che possono essere espresse nella forma

(e altre due equazioni simili per gli assi y e z). Le equazioni di Navier contengono una costante elastica ε e corrispondono alle equazioni generali della teoria lineare dell'elasticità sotto l'ipotesi di uguaglianza dei coefficienti di Lamé λ=μ=ε.

Nella seconda metà della sua memoria, Navier studia l'equilibrio di un corpo elastico (con la medesima formulazione molecolare), usando il principio degli spostamenti virtuali e ottiene di nuovo le stesse equazioni di equilibrio, oltre a un'espressione per le condizioni al contorno sulla superficie del corpo, dove viene data una certa distribuzione degli sforzi. In conclusione, Navier fornisce equazioni le quali descrivono le vibrazioni per un corpo elastico, aggiungendo termini inerziali appropriati.

Il ragionamento di Navier è trasparente ed elementare per quanto riguarda gli strumenti matematici impiegati, ma non privo di errori, relativi al passaggio formale dall'interazione delle molecole discrete all'integrazione sul volume. Proprio per questo aspetto fu immediatamente criticato e ben presto ci furono dei tentativi per apportare dei miglioramenti. In particolare, Poisson provò (senza però grande successo) a formalizzare in maniera rigorosa tutte le trasformazioni nel contesto di un modello molecolare 'puntuale'. Nonostante ciò, la meccanica moderna dei solidi deformabili prende inizio dal Mémoire sur les lois de l'équilibre di Navier.

Dinamica di un corpo elastico

Il 30 settembre 1822, a meno di un anno di distanza dalla presentazione della seconda memoria di Navier, Cauchy sottopose all'Académie di Parigi le Recherches sur l'équilibre et le mouvement intérieur des corps solides ou fluides, élastiques ou non élastiques (in forma ampliata questo lavoro venne pubblicato nel secondo e nel terzo volume dei suoi Exercices de mathématiques, 1827-1828).

Come si evince anche dal breve rapporto pubblicato all'inizio del 1823, Cauchy sviluppò nelle Recherches un approccio generale al problema dei continui. Egli introdusse il concetto di sforzo su una piastra, lo presentò in termini di tre componenti parallele agli assi delle coordinate cartesiane, e studiò lo stato di sforzo in un punto di un corpo elastico. Inoltre, utilizzando il metodo di Euler per l'isolamento di un elemento di volume e la successiva analisi delle forze agenti su di esso, Cauchy ottenne le equazioni generali dell'equilibrio dei mezzi continui, espresse in funzione degli sforzi, che, nella notazione per gli sforzi introdotta nel 1841 da Neumann, hanno la forma:

(più altre due equazioni analoghe per gli assi y e z) e dimostrò la proprietà di reciprocità degli sforzi: X_y=Y_x, X_z=Z_x, Y_z=Z_y. Studiando lo sforzo e lo stato deformato, egli mise in evidenza gli assi principali e trovò le quadriche degli sforzi e delle deformazioni. Così nel 1822 Cauchy creò lo strumento utilizzato ancora oggi con successo nella meccanica dei continui. Egli, tuttavia, non riuscì inizialmente a ottenere le equazioni generali della teoria dell'elasticità espresse in funzione degli spostamenti, poiché aveva adottato un'ipotesi piuttosto particolare secondo la quale in corrispondenza di ciascun punto di un corpo isotropo gli sforzi principali sono proporzionali (con un coefficiente identico) alle estensioni principali. Le equazioni con un'unica costante elastica come la [7] appaiono quindi equivalenti al caso di una costante di Lamé λ nulla.

Nel terzo volume degli Exercices de mathématiques di Cauchy si trova però anche un'ipotesi più generale secondo la quale gli sforzi principali dipendono linearmente dalle estensioni principali e dall'espansione volumetrica relativa in un punto. Cauchy non fornì argomenti in favore di questa ipotesi e tuttora non è chiaro se egli ne comprese la generalità. In ogni caso ottenne le equazioni classiche della dinamica per un corpo elastico isotropo espresse in funzione degli spostamenti, che (utilizzando la notazione introdotta da Lamé nel 1852) hanno la forma

(più altre due equazioni simili per gli assi y e z). Cauchy analizzò il significato fisico dei coefficienti λ e μ (K e 1/2k nella notazione di Cauchy). In particolare, egli prese in considerazione la compressione di un cilindro, calcolò la sua deformazione trasversale relativa e stabilì che essa è uguale a λ/2(λ+μ)⟨1/2. Si osservi che, nel caso delle equazioni di Navier, Poisson aveva rilevato in precedenza che questa quantità è uguale a 1/4. Tuttavia non si trova la formula del modulo di elasticità

la quale discende da correlazioni che vengono fornite nel lavoro di Cauchy.

In questo volume degli Exercices Cauchy cercò di stabilire le equazioni per un corpo elastico anisotropo con 9 costanti elastiche mediante un ragionamento più complesso, meno chiaro però di quello presentato da Navier nella sua breve nota (dal suo modello molecolare egli ottenne anche le equazioni classiche per un corpo isotropo con 2 costanti elastiche, tuttavia il procedimento utilizzato per ottenerle non era particolarmente rigoroso).

Un'analisi generale per un corpo anisotropo nel contesto dell'approccio molecolare, adeguato al metodo di Navier, fu sviluppata da Poisson: in un articolo pubblicato nel 1829, egli ottenne 36 coefficienti che determinano la dipendenza di sei componenti dello sforzo da sei componenti della deformazione. Nel 1839 Poisson ridusse queste 36 costanti a 15, che nel caso di un corpo isotropo si riducono all'unica costante di Navier.

Un approccio piuttosto diverso alle equazioni della teoria dell'elasticità venne sviluppato alla fine degli anni Trenta dell'Ottocento e nel decennio successivo in Inghilterra. George Green (1793-1841) pubblicò nel 1839 un saggio sulla teoria della propagazione della luce nel quale presentava la teoria di un etere elastico basata sul principio di conservazione dell'energia, da lui stesso formulato nel modo seguente: "Qualunque sia il modo in cui gli elementi di un sistema materiale possano agire gli uni sugli altri, se tutte le forze interne esercitate sono moltiplicate per gli elementi delle loro rispettive direzioni, la somma totale per ogni porzione assegnata della massa sarà sempre il differenziale esatto di una funzione". Più avanti, sempre nel medesimo saggio, Green mostra che questa funzione dovrebbe essere una funzione omogenea di secondo grado dei sei componenti della deformazione che contiene di conseguenza, nel caso generale, 21 costanti e, nel caso di un corpo isotropo, 2 costanti che caratterizzano le proprietà elastiche del corpo.

Un posto di rilievo nella storia della meccanica dei continui è occupato da George G. Stokes (1819-1903), il quale ottenne le equazioni della teoria dell'elasticità partendo da un approccio alla Euler-Cauchy e sulla base di un'ipotesi naturale di dipendenza lineare delle componenti dello sforzo da quelle della deformazione (Stokes 1845). Per un corpo isotropo egli ricavò 2 costanti elastiche sostenendo, con argomenti di un certo peso, che non potevano essere ridotte a una sola. Un'analisi più dettagliata di tale questione, con l'aggiunta di ragionamenti termodinamici, venne fornita da William Thomson (lord Kelvin, 1824-1907) nel corso degli anni Cinquanta del XIX secolo.

Pertanto, già nel 1830 erano stati ottenuti due sistemi per la teoria dell'elasticità in grado di caratterizzare un corpo elastico mediante 1 o 2 costanti elastiche (rispettivamente quelli di Navier e di Cauchy). Tutti gli autori francesi però, incluso Cauchy, pensarono in un primo momento che un corpo isotropo reale fosse caratterizzato da un'unica costante. Alla fine del decennio successivo entrambi i sistemi erano stati generalizzati a corpi anisotropi mediante l'introduzione di 15 e 21 costanti (Poisson e Green).

A partire dalla fine degli anni Quaranta si sviluppò una lunga discussione sul numero di costanti fisiche che descrivono un corpo elastico. I sostenitori della 'teoria multicostanti' dichiaravano che esistono 21 costanti per un corpo anisotropo e 2 per uno isotropo, mentre i sostenitori della 'teoria raricostanti' riducevano il numero rispettivamente a 15 e 1.

Si deve notare che la 'teoria multicostanti' trovò un gran numero di sostenitori dopo la comparsa delle Leçons sur la théorie mathématique de l'élasticité des corps solides (1852) di Gabriel Lamé (1795-1870). Il ruolo di Lamé in tale questione non fu determinato, tuttavia, dal fatto che le sue conclusioni fossero provate in maniera più rigorosa, ma esclusivamente dalla popolarità delle sue Leçons.

Per più di mezzo secolo furono intrapresi tentativi finalizzati a controllare sperimentalmente la validità di uno o dell'altro sistema di equazioni della teoria dell'elasticità. L'intero complesso delle ricerche sperimentali, e soprattutto i risultati ottenuti sulla base di considerazioni termodinamiche, portarono alla fine del XIX sec. al completo trionfo della 'teoria multicostanti'. Tuttavia, ancora nel 1885, l'ormai anziano Saint-Venant continuava a ostinarsi nel sostenere la 'teoria raricostanti' per i solidi reali.

Il trionfo della 'teoria multicostanti' generò tentativi di dedurre in maniera rigorosa le sue equazioni anche con l'aiuto di un modello molecolare. Tali tentativi, che sviluppavano il lavoro di Poisson, continuarono fino alla fine del XIX sec.; tuttavia solo Thomson mostrò elegantemente che, per ottenere 21 costanti, sarebbe stato necessario utilizzare un modello molecolare dotato di due reticoli a punti regolari, inseriti l'uno nell'altro. La giustificazione 'molecolare' rigorosa della teoria dell''elasticità multicostanti' fu ottenuta in questo modo soltanto da Max Born (1915).

Prima di passare in rassegna le soluzioni proposte per problemi specifici della teoria dell'elasticità, appare necessario spendere qualche parola riguardo alle formulazioni generali di questi problemi.

Le equazioni della teoria dell'elasticità contengono le derivate degli spostamenti, determinano cioè effettivamente le deformazioni del corpo. Tuttavia in un corpo elastico reale non può realizzarsi un qualunque campo di deformazioni, a causa della continuità degli spostamenti. Saint-Venant derivò le condizioni imposte da questa restrizione (le cosiddette 'condizioni di compatibilità') per le componenti della deformazione. Condizioni simili per le componenti dello sforzo furono ottenute nel corso degli anni Novanta da Eugenio Beltrami e, in forma più generale, da John H. Michell.

L'unicità delle soluzioni nei problemi della teoria dell'elasticità fu oggetto d'indagine da parte di Gustav Robert Kirchhoff. Quanto al problema dell'esistenza delle soluzioni stesse, esso si rivelò molto più complicato e venne risolto solamente nel corso del XX secolo.

Sviluppi teorici successivi e prime applicazioni

Le prime applicazioni dell'elastostatica a problemi particolari furono attuate dagli ingegneri francesi Lamé e Clapeyron, che a quel tempo stavano lavorando al servizio del governo russo a San Pietroburgo. Nel Mémoire sur l'équilibre intérieur des corps solides homogènes (1831) essi studiavano l'allungamento di un prisma infinito, la torsione di un cilindro circolare infinito, l'equilibrio di una sfera sotto l'azione di mutua attrazione delle sue particelle, l'equilibrio di un cilindro circolare cavo e di una sfera sotto l'azione di una pressione interna ed esterna. Lamé e Clapeyron introdussero anche alcuni integrali (con integrazione quadrupla) per risolvere problemi relativi a un semispazio, uno strato piano e un cilindro circolare infinito sotto l'azione di assegnate distribuzioni degli sforzi sulla loro superficie. Per trovare una soluzione a quest'ultimo problema, essi utilizzarono coordinate cilindriche (un ampio uso delle coordinate curvilinee è merito di Lamé, che nel 1859 dedicò un libro a tale argomento).

Nel corso del XIX sec. alcuni studi furono dedicati a vari problemi relativi a una sfera o a un cilindro elastici (continui e cavi), nei quali furono sviluppati metodi di espansione delle soluzioni in serie di funzioni sferiche e cilindriche. Tra i lavori teorici della prima metà del secolo si può ricordare anche un saggio realizzato da Jean-Marie-Constant Duhamel (1838) su come il riscaldamento non omogeneo di un corpo influisca sul suo stato di sforzo, che inaugurò una serie di lavori sulla termoelasticità.

Fin dal 1828 Cauchy e Poisson avevano applicato le equazioni generali per verificare la teoria elementare della flessione delle travi sottili e l'anno successivo Cauchy aveva ottenuto formule approssimate per la torsione di travi sottili rettangolari. Queste ricerche di Cauchy spinsero Saint-Venant a sviluppare la teoria generale della flessione e torsione di travi prismatiche, che divenne il più grande risultato pratico della teoria dell'elasticità intorno alla metà del XIX secolo.

I primi lavori di Saint-Venant sulla flessione e torsione delle travi risalgono agli anni Quaranta. La forma finale di questa parte della teoria dell'elasticità fu data da Saint-Venant in due memorie presentate all'Académie il 13 giugno del 1853 e il 20 giugno del 1855 (pubblicate nel 1856). Egli ottenne una soluzione per i problemi corrispondenti, introducendo nella teoria dell'elasticità un metodo seminverso estremamente fruttuoso (quando una parte degli spostamenti e degli sforzi è nota, e l'altra parte viene determinata tramite equazioni) e il principio di azione locale di un carico bilanciato staticamente, che più tardi hanno congiuntamente ricevuto il nome di 'principio di Saint-Venant'.

Avendo stabilito alcune proprietà degli spostamenti sulla base di considerazioni di carattere speculativo e assumendo l'assenza di componenti longitudinali degli sforzi di taglio sulle superfici laterali delle travi, Saint-Venant dimostrò la coerenza di tali ipotesi e ridusse il problema della torsione alla soluzione dell'equazione di Laplace per gli spostamenti longitudinali delle particelle in una sezione trasversale originariamente piana della trave; ridusse inoltre il problema della flessione alla soluzione dell'equazione di Poisson per una funzione ausiliaria (dove la distribuzione degli sforzi in corrispondenza delle facce terminali della trave veniva dedotta dalla soluzione). Saint-Venant considerò in dettaglio la torsione e la flessione di travi con sezioni trasversali ellissoidali e rettangolari oltre a molti altri problemi specifici. Un puro spirito ingegneristico è presente in tutti i suoi lavori: egli aspira a ridurre le soluzioni a un numero e a un diagramma, a studiare le porzioni di sezioni trasversali più pericolose, in termini di resistenza, e a fornire esempi di calcoli assolutamente chiari.

Le due memorie di Saint-Venant sopra menzionate aprirono un'epoca di ampie applicazioni ingegneristiche della teoria dell'elasticità. Un contributo significativo per il successivo sviluppo di questa teoria venne da Valentin-Joseph Boussinesq (1842-1929), un allievo di Saint-Venant. Nel suo ampio trattato Application des potentiels à l'étude de l'équilibre et du mouvement des solides élastiques (1885) sono presi in considerazione in maniera sistematica molti problemi relativi a corpi infiniti soggetti a certe forze o a spostamenti in un dominio piccolo (sulla superficie oppure all'interno del corpo). Per fornire soluzioni generali, Boussinesq utilizzò un insieme di soluzioni elementari determinate da vari potenziali (diretto, inverso e logaritmico). Egli considerò in forma generale il problema di un semispazio con tre componenti degli spostamenti (oppure degli sforzi), così come pure coppie di spostamenti (o sforzi) e uno sforzo (o spostamento) normale impartito in corrispondenza del contorno. Le sue soluzioni dei problemi relativi a un semispazio con un dato carico verticale e a quelli relativi alla pressione esercitata da uno stampo rigido sono di grande interesse pratico.

Nel medesimo campo, contemporaneamente a Boussinesq, operò l'ingegnere italiano Valentino Cerruti (1850-1909), il quale ottenne soluzioni molto simili avvalendosi delle funzioni di Green. Egli faceva parte di una fiorente scuola italiana di teoria matematica dell'elasticità che si sviluppò nel corso della seconda metà del XIX sec. e alla quale appartenevano anche: Luigi Federico Menabrea, Enrico Betti, Luigi Cremona, Eugenio Beltrami, Francesco Crotti, Alberto Castigliano e, di poco più giovani, Vito Volterra, Carlo Somigliana, Giuseppe Lauricella, Emilio Almansi.

Un settore autonomo della teoria dell'elasticità è rappresentato dai problemi piani. Un certo numero di risultati indipendenti fu ottenuto nel XIX sec., anche se i metodi generali per risolverli mediante l'uso della teoria delle funzioni analitiche sono stati sviluppati soltanto nel corso del XX secolo.

Il primo approccio decisamente generale ai problemi piani è contenuto nel trattato di Alfred Clebsch Theorie der Elasticität fester Körper (Teoria dell'elasticità dei corpi solidi, 1862), in cui egli prese in considerazione, in particolare, un problema piano relativo a una piastra rotonda. La soluzione di un problema piuttosto interessante che riguardava la flessione di una trave curvilinea (i cui contorni sono tracciati da archi di cerchi concentrici) fu fornita nel 1881 da Golovin. D'altra parte, già nel 1862 George B. Airy (1801-1892) aveva scoperto l'esistenza di una funzione, che ricevette il suo nome, le cui derivate seconde determinano le componenti dello sforzo in un problema piano, in assenza di forze volumetriche. Nel 1872 James C. Maxwell (1831-1879) specificò che questa funzione soddisfa un'equazione biarmonica. Studi dettagliati di problemi piani furono condotti da Michell che continuò le analisi di Maxwell sulla dipendenza delle soluzioni dalle costanti elastiche del materiale e diede, in particolare, una soluzione per il cuneo caricato con una forza localizzata nel suo vertice.

Vale la pena di ricordare il lavoro, del 1883, in cui Heinrich Rudolf Hertz (1857-1894) studiò un problema di contatto per un cilindro caricato in maniera uniforme con forze normali lungo il suo elemento.

Ampia attenzione fu dedicata nel corso dell'intero Ottocento alla teoria delle piastre e, alla fine del secolo, alla teoria dei gusci, cioè delle superfici strutturali curve. Le prime ricerche sulla flessione e sulle vibrazioni delle piastre erano state intraprese già nel corso del XVIII sec. da Euler e da Jakob II Bernoulli.

Furono studiate le equazioni per la flessione delle piastre, sulla base di un modello molecolare e delle equazioni generali della teoria dell'elasticità, di Poisson, Navier e Cauchy. Navier fornì nel 1823 un'equazione piuttosto rigorosa per la flessione statica di una piastra tanto nel caso di un carico normale, quanto in quello della deformazione sotto l'azione di forze al contorno agenti sul piano della piastra. Nel caso di una piastra rettangolare sostenuta liberamente, Navier ottenne una soluzione corretta utilizzando una serie trigonometrica doppia. Un'analisi generale delle condizioni al contorno fu eseguita nel 1829 da Poisson, che formulò però una condizione superflua sul contorno nel caso dell'esistenza di note forze esterne agenti su di esso.

L'insieme corretto di condizioni venne trovato successivamente da Kirchhoff nel 1850 e interpretato in modo chiaro dal punto di vista fisico da Thomson nel 1867. La teoria generale della flessione delle travi, così come una teoria delle piastre basata su ipotesi accurate vicine a un'ipotesi di sezioni piane nella teoria elementare della flessione, e inoltre una deduzione piuttosto rigorosa delle già note equazioni per le piccole deformazioni delle piastre mediante l'uso del principio dei lavori virtuali, sono tutte da attribuire a Kirchhoff, che in seguito, insieme a Clebsch, generalizzò la teoria per deformazioni non troppo piccole. Lo sviluppo della teoria dei gusci di curvatura arbitraria, adeguata alla costruzione di Kirchhoff, fu elaborata da Hermann Aron (1874), da August E.H. Love (1888) e da Alfred B. Basset (1890).

Energia potenziale di deformazione

Un impulso essenziale agli ulteriori sviluppi della teoria dell'elasticità, generale e applicata (e soprattutto della meccanica strutturale), fu fornito dall'introduzione di considerazioni di tipo energetico e, in particolare, di principî variazionali basati sull'analisi dell'energia della deformazione elastica.

Già nel 1750 Jacopo Francesco Riccati (1676-1754) aveva sottolineato l'esistenza di un'energia potenziale di deformazione. In realtà si trova un potenziale elastico nella memoria di Navier del 1821, nella derivazione delle equazioni della teoria dell'elasticità mediante l'uso del principio dei lavori virtuali. L'esistenza di un potenziale elastico fu postulata da Green nel 1837 e dimostrata da Thomson nel 1855 sulla base di considerazioni termodinamiche.

L'importante teorema di Clapeyron, che stabilisce che il lavoro esercitato dalle forze esterne è uguale al doppio dell'energia associata alla deformazione, ebbe un ruolo decisivo nell'applicazione di metodi basati su considerazioni energetiche. Sembra che questo teorema fosse stato enunciato da Clapeyron all'inizio degli anni Trenta dell'Ottocento, ma divenne di pubblico dominio soltanto nelle Leçons di Lamé.

Il teorema di Clapeyron si rivelò uno strumento conveniente per svariati calcoli di meccanica strutturale. Una delle sue prime applicazioni può essere trovata già in un lavoro di Bezpalov del 1855. Il metodo generale per il progetto di travature reticolari labili, che fu formulato in maniera astratta da Maxwell (1864) ed elaborato da Carl Friedrich Mohr negli anni 1874-1875, è basato sul teorema di Clapeyron.

Nel XIX sec. lo sviluppo di metodi energetici in teoria dell'elasticità è correlato strettamente al progetto di sistemi staticamente labili. A questo proposito molta attenzione fu posta alla fine del XIX sec. al metodo delle linee di influenza, introdotto in meccanica strutturale da Clemens Winkler e Mohr alla fine degli anni Sessanta. La loro costruzione si basa sul teorema di reciprocità, formulato in un caso elementare da Maxwell, e generalizzato nel caso di condizioni arbitrarie di equilibrio da Betti nel 1872 e per la vibrazione dei sistemi elastici da Rayleigh nel 1873. A quest'ultimo si deve anche un'ampia utilizzazione del concetto di forze e spostamenti generalizzati, che giocò un ruolo importante nello sviluppo successivo della teoria dell'elasticità applicata. In particolare, V.L. Kirpičev nel 1884 applicò i teoremi di reciprocità, introducendo le forze generalizzate per progettare travi continue e archi.

Il concetto di energia di deformazione ha permesso di definire metodi variazionali efficaci per l'analisi di sistemi staticamente indeterminati (generalizzati successivamente a qualunque sistema elastico). Originariamente ciò venne realizzato nel 1858 per alcune travature reticolari dall'ingegnere italiano Menabrea. Una teoria generale fu elaborata nel 1865 da James H. Cotterill e, indipendentemente, in studi degli anni 1873-1875, da Alberto Castigliano. Alcune ambiguità nel lavoro di quest'ultimo suscitarono tra gli ingegneri tedeschi lunghe discussioni, alle quali parteciparono attivamente Mohr e Heinrich Müller-Breslau (1851-1925). Quest'ultimo fece notare, in particolare, che in molti casi i risultati dell'analisi ricavati applicando i teoremi di Castigliano coincidevano con quelli ottenuti con calcoli diretti utilizzando il metodo di Maxwell-Mohr. Un'analisi rigorosa di entrambi i metodi fu fornita all'inizio degli anni Ottanta nei lavori di Crotti, il quale formulò un principio abbastanza generale per l'energia addizionale di deformazione.

Queste ricerche sui principî variazionali nella teoria dell'elasticità giunsero a una certa conclusione all'inizio del XX sec., quando Born enunciò il suo principio variazionale canonico (1906), che più tardi sarà applicato a problemi generali di elasticità da Ernst Hellinger (1914).

Un approccio generalizzato ai principî di energia variazionale nella teoria dell'elasticità fu poi adottato da Prange nel 1919. Per questo motivo il principio variazionale più generale della teoria dell'elasticità è talvolta denominato 'principio canonico dell'energia potenziale di Born-Prange'.

Resistenza dei materiali e meccanica strutturale

La precedente rassegna sullo sviluppo della teoria dell'elasticità nel XIX sec. sarebbe ovviamente incompleta se non ci si soffermasse, almeno brevemente, sui metodi ingegneristici per l'analisi della resistenza dei materiali nonché sulla meccanica strutturale.

Si possono trovare alcuni problemi elementari di resistenza dei materiali perfino in lavori che risalgono al XVIII secolo. I primi libri di testo in questo campo apparvero all'inizio dell'Ottocento. Nel Résumé des leçons (1826) di Navier incontriamo progressi fondamentali per almeno due aspetti. Prima di tutto, Navier fornisce un metodo generale per l'analisi di problemi staticamente indeterminati, che consistono nell'analisi delle deformazioni degli elementi di una struttura e sulla base della quale si ottengono equazioni aggiuntive (la prima analisi di travi continue si deve a Johann Albert Eytelwein, 1805-1808). Il libro di testo di Navier contiene anche una teoria della flessione di travi curvilinee che è basata sull'ipotesi Bernoulli-Euler di proporzionalità fra i momenti di flessione e l'incremento della curvatura della trave.

Non si trova tuttavia nel testo di Navier alcun calcolo relativo alla flessione obliqua di travi dotate di sezioni trasversali asimmetriche, sebbene, per esempio, la compressione eccentrica di colonne rettangolari fosse già stata presa in considerazione da Young nel 1807. Il ruolo degli assi principali di inerzia della sezione trasversale fu chiarito dagli ingegneri francesi solamente nei primi anni Quaranta del XIX secolo.

È necessario notare che all'inizio dell'Ottocento lo studio della flessione delle travi non prendeva in considerazione le forze di taglio nelle sezioni trasversali. Jean-Victor Poncelet (1788-1867) le esaminò parzialmente, ma una teoria completa degli sforzi di taglio nelle travi fu sviluppata solamente nei tardi anni Quaranta da Žuravskij, e successivamente inclusa nei libri di testo sulla resistenza dei materiali.

Il progetto di sistemi staticamente indeterminati attirò l'attenzione degli ingegneri nel corso dell'intero secolo. In particolar modo, Clapeyron suggerì l'idea dell''equazione dei tre momenti' per le travi orizzontali continue (1849-1850), che nel corso degli anni Sessanta fu generalizzata da Mohr e Jacques-Antoine-Charles Bresse (1822-1883) a travi con differente altezza dei supporti. L'analisi di sistemi d'aste statisticamente indeterminati ebbe inizio grazie agli studi di Clebsch (1862).

Lo sviluppo della teoria della flessione di una trave curvilinea, con applicazioni al progetto di archi, è legato a lavori di Saint-Venant, Bresse e Winkler. Quest'ultimo propose anche il primo progetto di travi su fondazione elastica basandosi sull'ipotesi di una relazione di proporzionalità tra la flessione della trave e il carico.

A metà del XIX sec. il progetto delle travature reticolari divenne un problema urgente della meccanica strutturale legato all'intensificarsi della costruzione di ponti. In origine, erano stati definiti metodi analitici per la loro analisi (Johann Wilhelm Schwedler, Karl Ritter von Ghega e altri). Più tardi la teoria dei sistemi d'aste è servita come fonte per lo sviluppo della statica grafica. Il metodo del poligono reticolare venne introdotto in modo sistematico in meccanica strutturale da Karl Culmann nel suo Die graphische Statik (La statica grafica, 1866). I criteri per la costruzione di diagrammi di forza per le travature reticolari furono individuati da Maxwell e introdotti in Europa, nel 1872, grazie all'opera di Cremona che ne diffuse l'utilizzazione nella pratica.

L'analisi generale delle travature reticolari isostatiche venne sviluppata da Mohr, Müller-Breslau e Lebrecht Henneberg. Un approccio originale per usare il principio degli spostamenti virtuali nel progetto delle travature reticolari fu elaborato ulteriormente da Nikolaj Egorovič Žukovskij nel 1909.

È possibile situare nella seconda metà del XIX sec. la formulazione dei primi problemi di progetto ottimale (travature reticolari di peso minimo, sezioni ottimali, ecc.). Una parte importante della meccanica strutturale riguarda l'analisi della stabilità e della deformazione; essa è stata effettuata nel corso degli anni Ottanta a opera di Felix S. Jasinski, e in seguito, da Friederich Engesser. Contemporaneamente, una teoria generale della stabilità delle piastre elastiche fu sviluppata da George H. Bryan nel 1888.

Un settore indipendente della teoria delle strutture era costituito, nell'Ottocento, dalla teoria della pressione di un terreno, i primi metodi elementari per il calcolo della pressione, basati sull'analisi dei piani di rottura furono presentati nel XVIII sec. da Charles-Augustin Coulomb (1736-1806) e Reinhard Woltmann (1757-1837). Nel 1820 Jacques-Frédéric Français prese in considerazione un caso di terreni compatti e in seguito, nel 1846, Alexandre Collin elaborò una teoria generale della pressione di un terreno reale (coesivo) con superfici di rottura curve. I successivi approfondimenti di quest'area della meccanica nel corso del XIX sec. si limitarono a varie riformulazioni dei risultati precedenti e allo sviluppo di metodi convenienti di progetto di tipo analitico (Rankine, Rebchan) e soprattutto grafico (Jean-Victor Poncelet, Culmann, Engesser).

Non ci si soffermerà qui sui progressi delle tecniche sperimentali per l'analisi delle strutture che giocarono un ruolo significativo nello sviluppo della teoria delle strutture. Tuttavia va menzionato un importante filone nelle ricerche di laboratorio, legato all'uso di metodi di tipo ottico nello studio degli sforzi. All'inizio del XIX sec. fu scoperta la presenza di una doppia rifrazione in materiali trasparenti soggetti all'azione di sforzi. Una teoria dettagliata relativa a una tecnica ottica che permettesse lo studio degli sforzi, basata su questo fenomeno, venne elaborata da Franz Ernst Neumann nel 1842. Alcuni brillanti esperimenti, che sfruttavano l'impiego della tecnica della fotoelasticità, furono condotti da Maxwell nel 1853. Una ripresa di questo metodo, nell'ambito di ricerche di ingegneria applicata, si sviluppò tuttavia soltanto all'inizio del XX secolo.

Tutti i problemi di resistenza dei materiali sono ridotti alla definizione degli sforzi e delle deformazioni di strutture elastiche sotto l'azione di un certo carico, entro i limiti di qualche schema semplificato. I compiti di progetto pratico consistono solitamente nella definizione del carico massimo ammissibile sulle strutture, e ciò richiede l'introduzione di criteri appropriati di frattura dei materiali.

Agli inizi era lo sforzo (normale) massimo a essere solitamente considerato come il criterio di frattura. A metà del XIX sec. fu definito il principio delle deformazioni massime, diffuso nel Continente per effetto dell'influenza della scuola francese (Poncelet, Saint-Venant), mentre gli inglesi continuavano in gran parte a sostenere il criterio degli sforzi massimi. Numerose ricerche sperimentali condotte negli ultimi anni del XIX sec. convinsero tuttavia gli ingegneri dell'inadeguatezza di entrambe queste teorie. Gli esperimenti rivelarono che gli sforzi di taglio massimo rivestono un ruolo importante nei processi di frattura. George H. Darwin aveva proposto una teoria della differenza massima degli sforzi normali, che appariva vicina alla teoria degli sforzi di taglio massimi. Una teoria della resistenza maggiormente adeguata dal punto di vista fisico fu presentata da Maksymilian Tytus Huber, il quale introdusse come criterio di frattura un'energia associata alla deformazione.

Soltanto all'inizio del XX sec. fu scoperta l'esistenza di due processi radicalmente diversi, uno per i materiali fragili e l'altro per quelli duttili (plastici), aprendo così una nuova strada per lo sviluppo della moderna meccanica della frattura.

Negli anni Trenta dell'Ottocento, furono osservati sperimentalmente i fenomeni di creep (scorrimento) dei materiali e il conseguente effetto elastico. Lo studio di questi fenomeni condusse a modelli non classici dei solidi deformabili. I più significativi tra essi furono quelli derivanti dagli studi sull'effetto viscoso nei solidi (Poncelet, Saint-Venant), che produssero una serie di modelli per i solidi deformabili e la nascita di una nuova scienza fisico-meccanica chiamata reologia. L'osservazione delle proprietà plastiche dei metalli fu particolarmente importante e favorì lo sviluppo della meccanica dei corpi deformabili. Il lavoro sperimentale portato avanti da Henri Édouard Tresca nel corso degli anni Sessanta dell'Ottocento diede a Saint-Venant l'opportunità di proporre la prima teoria matematica della plasticità, basata su ipotesi di incomprimibilità del materiale, di coincidenza delle direzioni delle deformazioni principali e degli sforzi principali e di costanza dello sforzo di taglio massimo in ciascun punto (1870-1871).

In una rassegna sui metodi per la stima della resistenza dei materiali nel corso dell'ultimo trentennio del XIX sec., appare necessario sottolineare l'importante ruolo assunto dalla scuola ingegneristica tedesca della quale alcuni rappresentanti di maggior spicco sono già stati menzionati (Winkler, Mohr, Müller-Breslau, Föppl). All'inizio del Novecento fu fondata in Germania la nuova scuola di Gottinga, che diede alla meccanica molti scienziati di grande importanza come Ludwig Prandtl e Theodore von Kármán. Contemporaneamente anche in Russia si formò un'importante scuola ingegneristica sotto l'influsso di V.L. Kirpičev, il cui più autorevole rappresentante fu Stephen Timoshenko.

Idrodinamica di un fluido viscoso

Nella storia dell'idrodinamica, la prima metà del XIX sec. è caratterizzata da tentativi di generalizzare il concetto di fluido ideale. L'introduzione del modello di fluido viscoso non avvicinò l'idrodinamica dell'Ottocento alla soluzione di un vasto campo di problemi pratici, essendo dovuta soltanto all'intenzione di analizzare i problemi di ingegneria idraulica e, prima di tutto, la natura della resistenza al flusso.

Alla base della definizione di fluido ideale c'era l'ipotesi che la pressione su un elemento di un piano qualunque dovesse essere normale al piano, oppure che la pressione in ogni punto non dovesse dipendere dalla sua direzione rispetto al piano. La generalizzazione di questa definizione fu ottenuta mediante l'introduzione degli sforzi di taglio in un fluido in moto.

Fu Navier a fare il primo passo per la creazione dell'idrodinamica di un fluido viscoso. Egli, in un saggio del 1822, introdusse un approccio molecolare, simile a quello adottato nella sua derivazione delle equazioni della teoria dell'elasticità, qui però complicate dal fatto che si doveva tener conto del moto del mezzo. Come ipotesi fondamentale egli accettò, seguendo, in termini generali, Newton, la proporzionalità della forza di interazione aggiuntiva delle molecole con la velocità dei loro reciproci avvicinamenti o allontanamenti. Per effetto di questa ipotesi, la forza di interazione tra le molecole è definita secondo Navier nella forma f(ϱ)∙V, dove f(ϱ) è una funzione della distanza ϱ tra le molecole che decresce rapidamente al crescere di ϱ, e V è la velocità di mutuo avvicinamento. Utilizzando il principio degli spostamenti virtuali, esattamente come nella seconda metà della sua memoria riguardante il problema di un solido deformabile, e considerando solamente un fluido incomprimibile, Navier ottenne l'equazione del moto in una forma abbastanza moderna

(e due equazioni simili per gli assi y e z), dove

è una caratteristica fisica delle proprietà del fluido, che, come egli dimostrò, determina lo sforzo di taglio specifico per uno spostamento parallelo di strati adiacenti di fluido, e coincide con il coefficiente di Newton di viscosità dinamica.

Le equazioni di Navier furono generalizzate da Poisson nella memoria presentata all'Académie des Sciences nel 1829, nella quale egli cercava di fornire una deduzione rigorosa di tutte le equazioni della meccanica di un mezzo continuo, basandosi costantemente e coerentemente su un modello molecolare discreto. In tale memoria Poisson presentò una serie di risultati essenziali in idrodinamica. In particolare ricavò per la prima volta il sistema di equazioni per il moto di un fluido viscoso comprimibile, tenendo conto dell'effetto del trasferimento di calore.

Egli ottenne queste equazioni sulla base di un'analisi originale della deformazione delle particelle in un intervallo di tempo infinitamente piccolo, in cui ogni deformazione elementare viene rappresentata come costituita da due processi ‒ una deformazione elastica che soddisfa le equazioni di elasticità e una successiva ridistribuzione (equalizzazione) delle pressioni nel fluido. Questo ragionamento portò Poisson alla conclusione che gli sforzi di taglio sono proporzionali alle velocità di deformazione delle particelle. Egli ottenne così equazioni di moto che contenevano formalmente non due, ma tre caratteristiche fisiche del fluido (oltre alla densità). Questo fatto può essere spiegato mediante l'assenza di una definizione sufficientemente rigorosa riguardo alla pressione di equilibrio in un fluido viscoso. Per un fluido leggermente comprimibile e per il moto di un gas adiabatico, Poisson ridusse il numero di caratteristiche fisiche indipendenti a due; in questo modo, le sue equazioni del moto assunsero una forma vicina a quella delle equazioni esatte del moto per un fluido viscoso.

Sebbene Poisson avesse assunto come base un modello molecolare per la sua dimostrazione, bisogna notare che nei ragionamenti successivi egli usò concetti che fondamentalmente avevano a che fare con il continuo. Nella sua memoria si trovano così le equazioni differenziali di Cauchy del moto espresse in funzione delle componenti dello sforzo, e la dipendenza lineare di queste dalle velocità di deformazione. Tuttavia l'assenza di un trattamento puramente continuo di queste relazioni complicò notevolmente il ragionamento di Poisson.

Egli aggiunse l'equazione di continuità di Euler alle sue tre equazioni del moto, per poi passare all'analisi della distribuzione del calore nel flusso e scrivere l'equazione per il bilancio di calore (energia termica). Considerò quindi separatamente il moto di fluidi leggermente comprimibili e quello dei gas, distinguendo per questi ultimi i processi isotermi da quelli adiabatici.

Nel lavoro di Poisson si incontra quindi per la prima volta un'analisi piuttosto generale del moto dei fluidi, dove per raggiungere la completezza mancano solo la legge di conservazione dell'energia e l'equivalente meccanico del calore.

Un approccio di tipo continuo alla derivazione delle equazioni di Navier fu introdotto per la prima volta da Saint-Venant in una breve nota pubblicata nel 1843. Egli vi formulò in maniera esplicita l'ipotesi generalizzata di Newton secondo la quale gli sforzi di taglio sono proporzionali alle velocità di deformazione e di spostamento delle particelle precisando, senza scrivere esplicitamente le equazioni finali, che le equazioni generali del moto di un fluido si ottengono sostituendo nelle equazioni di Cauchy del moto le dipendenze lineari per le componenti degli sforzi:

dove

Stokes nel 1845 completò l'idrodinamica di un fluido viscoso. Indipendentemente da Poisson e Saint-Venant, egli fornì una deduzione rigorosa delle equazioni del moto di un fluido viscoso, basata sulla dipendenza lineare delle tre componenti dello sforzo dalle tre componenti della velocità di deformazione di una particella fluida.

Stokes ipotizzò che il fluido fosse un mezzo in cui la differenza tra la pressione su un elemento di un piano orientato arbitrariamente e la pressione media, esistente in condizioni di equilibrio relativo, è definita solamente dalla velocità di deformazione relativa della particella. Egli pervenne così a equazioni che contengono in generale due coefficienti di viscosità. Tuttavia Stokes, sulla base di un certo numero di argomenti, considerò nullo il secondo coefficiente della viscosità, e formulò le equazioni nella forma (più due equazioni simili per gli assi y e z):

La questione relativa al secondo coefficiente di viscosità rimase completamente aperta nel corso di tutto il XIX sec.; ma le ricerche sull'equazione di Navier-Stokes furono condotte nell'ipotesi di assenza del secondo coefficiente di viscosità e, di regola, per i fluidi incomprimibili, situazione in cui il coefficiente non dovrebbe in alcun modo entrare nelle equazioni del moto. La discussione sul secondo coefficiente di viscosità riprese solamente nel corso degli anni Novanta dell'Ottocento, per opera di Woldemar Voigt.

Le condizioni al contorno sono importanti per risolvere problemi specifici del moto di un fluido viscoso. Inizialmente non era chiaro se vi fosse aderenza dei fluidi viscosi in un flusso su superfici rigide. Tale questione rimase oscura per un lungo periodo e le prime soluzioni date da Navier e Stokes per il flusso in tubi circolari contengono un parametro che caratterizza lo scivolamento del fluido lungo le pareti. Negli anni Cinquanta dell'Ottocento Stokes, sulla base di considerazioni fisiche ragionevoli, giunse alla conclusione dell'adesione delle particelle fluide a pareti rigide. La discussione su questo argomento continuò tuttavia fino alla fine del XIX secolo. Le condizioni al contorno con lo scivolamento del fluido lungo le pareti furono utilizzate nel 1900 da Nikolaj Pavlovič Petrov nel suo articolo sulla lubrificazione idrodinamica nelle macchine e dispute sporadiche sull'attrito di scivolamento 'esterno' in un fluido viscoso sotto condizioni normali si svolsero anche nel XX secolo.

Nel corso dell'Ottocento si ottennero solamente poche e semplici soluzioni esatte delle equazioni di Navier-Stokes per un fluido incomprimibile. La prima fu la soluzione per un flusso stazionario in tubi cilindrici, che venne ottenuta nel 1822 da Navier stesso integrando l'equazione di Poisson per le componenti longitudinali della velocità. Navier non affrontò però l'integrazione nel caso di un tubo curvo. Una soluzione analitica per il flusso laminare in un tubo curvo con distribuzione parabolica di velocità fu ottenuta nel 1845 da Stokes. Soluzioni per altre sezioni trasversali del tubo furono dedotte successivamente.

Il flusso lento dell'acqua in tubi molto sottili (capillari) venne studiato sperimentalmente da Gotthilf Heinrich Ludwig Hagen nel 1839 e, con cura particolare, da Jean-Léonard-Marie Poiseuille (1840-1841), il quale stabilì per lo scarico dell'acqua la formula empirica riportata di seguito

dove T° è la temperatura, D e L rispettivamente il diametro e la lunghezza del tubo, P la differenza di pressione.

I risultati di Poiseuille confermano in maniera eccellente la soluzione teorica

e forniscono anche con elevata accuratezza la dipendenza della viscosità dell'acqua dalla temperatura.

Una soluzione per il moto di un fluido viscoso tra cilindri coassiali rotanti fu fornita da Stokes. In particolare egli focalizzò la propria attenzione su un errore commesso da Newton nei Principia (1687), relativo alla soluzione del problema della rotazione a simmetria assiale di un fluido viscoso infinito, già notato da Daniel Bernoulli.

Problemi relativi all'oscillazione di un corpo in un fluido viscoso e di un fluido viscoso in una sfera furono risolti nel caso di piccoli moti (Stokes, Maxwell, Helmholtz) e queste soluzioni furono utilizzate per controllare sperimentalmente le equazioni del moto. La giustificazione più convincente delle equazioni dell'idrodinamica di un fluido viscoso consiste, forse, nel notevole accordo tra gli esperimenti e il semplice risultato teorico relativo alla scarica di un fluido attraverso un tubo capillare.

Nel 1851 Stokes prese in esame un caso di moto non stazionario di un fluido viscoso, quando le equazioni generali degenerano nell'equazione di trasferimento di calore per l'unica componente della velocità diversa da zero. Uno sviluppo di questa linea di ricerche è opera di Rayleigh (1880) ed è collegato alla prima analisi della diffusione di vortici in un fluido viscoso e alla stabilità del moto laminare. La ricerca sulla dissipazione di energia in un fluido viscoso progredì in seguito grazie agli studi di Rayleigh, ma deriva anch'essa dal lavoro di Stokes del 1851. Bisogna ricordare anche un lavoro del 1873, legato a entrambi i precedenti argomenti, dovuto a Dmitrij Kostantinovič Bobylev, il quale investigò il ruolo delle forze viscose nel moto vorticoso dei fluidi.

Gli sviluppi successivi dell'idrodinamica di un fluido viscoso andarono in diverse direzioni. La linearizzazione elementare delle equazioni del moto, nelle quali venivano esclusi tutti i termini di convenzione, è dovuta a Stokes (1851). In quel lavoro egli risolse il problema della caduta uniforme di una palla in un fluido viscoso illimitato, e ottenne la ben nota formula per la resistenza che il fluido oppone alla palla: W=6πμaV (dove a è il raggio della palla e V è la velocità di caduta), ampiamente utilizzata ancora oggi nell'analisi dei dati dei viscosimetri. La soluzione di Stokes fu generalizzata più tardi al moto uniforme di un ellissoide. La linearizzazione ha però un campo di applicazione molto limitato e dà risultati contraddittori, per esempio, nel caso di un problema piano simile riguardante la caduta di un cilindro infinito.

Nel XIX sec. le equazioni di Navier-Stokes trovarono applicazioni pratiche soltanto nell'ambito della teoria idrodinamica della lubrificazione che si sviluppò verso la fine del secolo. Le prime ricerche in questo campo sono opera di Petrov (1883) e Osborne Reynolds (1886). Le equazioni di Navier-Stokes per uno strato sottile vengono semplificate, cancellando i termini di primo grado che contengono lo spessore relativo ε e il fattore ε2∙R_e (R_e è il numero di Reynolds). Le soluzioni relative al problema della teoria idrodinamica della lubrificazione offerte da Arnold Sommerfeld, Nikolaj Egorovič Žukovskij e Sergei Alekseevič Čaplygin risalgono all'inizio del XX secolo.

Una delle più importanti questioni dell'idrodinamica di un fluido viscoso è quella relativa ai vari regimi di flusso. Fin dalla prima metà del XIX sec. fu scoperto sperimentalmente che i moti di un fluido viscoso alle basse e alle alte velocità differiscono strutturalmente gli uni dagli altri.

Un settore speciale dell'idrodinamica è la teoria del moto dell'acqua sotterranea, cioè l'idrodinamica dei mezzi porosi, che è, in termini generali, correlata all'idrodinamica di un fluido viscoso. Tra i suoi fondamenti c'è una legge lineare per l'infiltrazione formulata nel corso degli anni Cinquanta dell'Ottocento dall'ingegnere francese Henri Darcy (nota, appunto, come 'legge di Darcy'), che stabilisce la proporzionalità tra la velocità di infiltrazione e il gradiente di pressione. Una teoria idraulica dello stato stazionario dell'acqua sotterranea, equivalente all'idraulica delle tubazioni e dei canali, fu proposta nel 1863 dall'ingegnere francese Jules Dupuit. Ulteriori progressi della teoria dell'infiltrazione durante il XIX sec. furono dovuti ai lavori di Philipp Forchheimer, il quale generalizzò la legge di Darcy ai flussi tridimensionali e ridusse i problemi planari per l'acqua sotterranea, confinata e libera, in mezzi omogenei, all'integrazione dell'equazione bidimensionale di Laplace. La generalizzazione della teoria idraulica al flusso non stazionario dell'acqua sotterranea con superficie libera fu opera di Boussinesq all'inizio del XX secolo.

Le equazioni generali della teoria dell'infiltrazione idrodinamica furono studiate nel 1889 da Žukovskij, il quale sostituì l'effetto dell'attrito viscoso in un flusso con forze volumetriche equivalenti, determinate in accordo con la legge di Darcy. In questo modo l'idrodinamica di un flusso viscoso nei mezzi porosi fu ridotta all'idrodinamica di un fluido ideale fittizio sotto l'azione di forze addizionali, proporzionali alla velocità di flusso e dirette nel verso opposto al moto, dimostrando così che l'equazione generale del moto (trascurando i termini inerziali) è l'equazione di Laplace. La teoria dell'acqua sotterranea è diventata un ramo indipendente dell'idrodinamica grazie ai lavori pubblicati nel 1899 dall'idrogeologo americano Charles S. Slichter.

Per concludere, ci si soffermerà a descrivere il problema generale della determinazione della similitudine nei processi idrodinamici sulla base delle equazioni di Navier-Stokes. Come è noto, alcuni concetti di similitudine nei problemi elementari di resistenza furono considerati già nel XVII sec. da Galilei nei suoi Discorsi (1638) e un criterio più generale di similitudine dinamica fu formulato nei Principia di Newton. Nella teoria del calore, anche Jean-Baptiste-Joseph Fourier (1768-1830) utilizzò ampiamente un criterio di similitudine. Tuttavia, sembra che l'analisi delle equazioni generali dell'idrodinamica dal punto di vista della similitudine non sia stata affrontata in maniera più o meno sistematica fino alla metà del XIX sec., quando Stokes provò a formulare principî generali per la similitudine dinamica in idrodinamica. Tale analisi fu condotta nel 1873 più dettagliatamente da Helmholtz, il quale utilizzò alcuni dei suoi risultati per verificare direttamente diversi esperimenti. Anche questo lavoro però non portò a un'introduzione generalizzata dei metodi di similitudine in idrodinamica. Questo processo ebbe luogo lentamente, le discussioni teoriche intorno ai fondamenti dei metodi di similitudine e dimensionali si estesero fino ai primi decenni del Novecento e l'introduzione pratica, per esempio, del numero di Reynolds, nei calcoli di progettazione ingegneristica, fu completata solo alla fine degli anni Venti del XX secolo.

Flussi vorticosi

Lo sviluppo fondamentale dell'idrodinamica di un fluido ideale comincia nel XIX secolo. Nel 1781 Lagrange aveva formulato l'importante teorema secondo il quale, sotto l'azione di forze dotate di un potenziale, il flusso di un fluido barotropico ideale, che a un certo istante di tempo possiede un certo potenziale di velocità, mantiene tale potenziale per sempre. Questo teorema determina immediatamente una classe di flussi potenziali e la sua importanza è spiegata, per esempio, dal fatto che tutti i flussi di un fluido ideale che cominciano da uno stato di riposo sono potenziali.

Il primo esempio di moto fluido potenziale venne fornito verso la metà del Settecento da Euler. Le ricerche sulla cinematica dei mezzi continui condotte successivamente da Cauchy e Stokes portarono alla formulazione del concetto di vortice e allo studio dei flussi vorticosi. Alcuni teoremi eleganti e importanti sulle linee e sui tubi di vortice furono pubblicati nel 1858 da Helmholtz. Il concetto di circolazione di velocità fu introdotto nel medesimo periodo e venne stabilito il legame tra la circolazione e il flusso vorticoso. Helmholtz dimostrò, in particolare, l'importante teorema cinematico sulla costanza del flusso lungo un tubo vorticoso, che comporta l'impossibilità della distruzione di quest'ultimo all'interno del dominio del flusso.

Helmholtz mostrò, per un fluido ideale incomprimibile, che in un campo conservativo di forze le linee di vortice sono costituite sempre dalle medesime particelle e che l'intensità dei tubi di vortice (il flusso vorticoso) è costante. Egli ottenne le sue dimostrazioni riducendo le equazioni di un moto fluido a una forma che, in notazione vettoriale, può essere così scritta

dove Ω e V sono i vettori di velocità del vortice e del flusso. Nel 1869 Thomson generalizzò i teoremi di Helmholtz a qualunque fluido barotropico.

Se i vortici esistono solo in un volume limitato di fluido e il fluido stesso è incomprimibile (o la variazione di volume del fluido avviene anch'essa in un volume limitato di spazio), la distribuzione del vortice Ω (e la divergenza θ) determina la velocità V del fluido in questo modo:

[19]  V=gradφ+rotH,

dove

essendo dτ l'elemento di volume e r la distanza dall'elemento di volume del punto in considerazione (questa rappresentazione fu data da Helmholtz nel caso θ=0).

L'introduzione delle componenti di vortice nelle equazioni dell'idrodinamica ottenne come risultato la loro completa analogia con le equazioni dell'elettromagnetismo, richiamando l'attenzione sull'argomento alla metà del XIX sec. (per es., il Treatise on electricity and magnetism di Maxwell del 1873). Le [19] e [20] hanno un ovvio parallelo nelle formule di Biot-Savart.

Discutendo varie forme dell'equazione del moto di un fluido con vortici, è ragionevole notare le utili trasformazioni delle equazioni dell'idrodinamica che furono introdotte negli anni Cinquanta dell'Ottocento da Clebsch, e nel decennio successivo da Heinrich Weber. L'equazione di Clebsch è una generalizzazione dell'integrale di Bernoulli, che presenta una certa analogia con le equazioni canoniche di Hamilton, mentre la trasformazione di Weber fornisce una forma modificata delle equazioni del moto espressa nelle cosiddette 'variabili' di Lagrange. Ricordiamo inoltre una forma delle equazioni di flusso trovata nel 1879 da Horace Lamb, che può essere scritta in notazione vettoriale nel modo seguente:

Un'analisi approfondita di una classe speciale di flussi vorticosi ‒ i cosiddetti 'flussi a elica', che si generano quando le direzioni dei vortici e delle velocità coincidono ‒ fu fornita nel 1881 da Ippolit Stepanovič Gromeka. Questa classe di flussi, esaminata successivamente anche da Beltrami, è degna di nota per il fatto che l'integrale di Bernoulli mantiene un valore costante nell'intero dominio di flusso. I flussi a elica sono quindi in un certo senso una generalizzazione naturale dei flussi potenziali.

Gli sviluppi di maggior rilievo furono ottenuti nel corso del XIX sec. proprio nell'ambito delle ricerche sui flussi fluidi potenziali. Per la costruzione di flussi di questo tipo (così come per quelli dei campi elettrostatici che formalmente a essi corrispondono) fu proposto il metodo delle sorgenti e dei pozzi, che risaliva sostanzialmente a una memoria di Green del 1828, e il metodo di riflessione delle singolarità che, nel 1843, attrasse l'attenzione di Stokes per le sue applicazioni idrodinamiche. L'ulteriore elaborazione di quest'ultimo metodo fu opera di Thomson e Kirchhoff.

Un ulteriore progresso nello sviluppo dell'idrodinamica negli ultimi trent'anni del XIX sec. fu favorito dallo studio del moto di un corpo rigido in un fluido ideale. Negli anni Sessanta Thomson e Kirchhoff considerarono il fluido e il corpo come un sistema dinamico accoppiato e ottennero le equazioni generali del moto del corpo in un fluido. I difficili problemi di integrazione di queste equazioni, strettamente connesse con questioni generali di dinamica dei corpi rigidi, hanno attirato l'attenzione di molti matematici applicati che lavoravano nel campo della meccanica (Clebsch, Lamb, Alfred G. Greenhill, Čaplygin, Vladimir Andreevič Steklov e altri). I risultati generali di questi lavori, che sono abbastanza complicati, non saranno presentati in questa sede salvo un'importante conclusione della teoria del moto di un corpo rigido in un fluido, secondo la quale l'effetto del fluido sul corpo in moto è equivalente a un aumento della sua massa inerziale (del valore della cosiddetta 'massa apparente'). Questa circostanza in origine fu scoperta in un esempio specifico, quello del moto di una sfera in un fluido, studiato negli anni Trenta da Green e nel decennio successivo da Stokes. La loro analisi mostrava, in particolare, che la massa apparente di una sfera nel suo moto di traslazione in un fluido illimitato è pari a metà della massa del fluido nel volume della sfera.

Grande attenzione fu dedicata nel corso del XIX sec. all'analisi di problemi particolari più semplici ‒ il moto di una sfera, di un ellissoide, di due sfere, ecc. in un fluido ‒ da Peter Gustav Lejeune Dirichlet, Clebsch, Thomson, Carl Anton Bjerknes, Kirchhoff, Carl Gottfried Neumann, Basset e altri.

La teoria delle figure di equilibrio di un fluido rotante, nata in connessione con lo studio della forma della Terra e di altri corpi celesti, divenne una parte indipendente dell'idrodinamica di un fluido ideale incomprimibile. Un approccio statico alla ricerca della forma della Terra risale a Newton (1687) e ad Alexis-Claude Clairaut (1743). Le prime ricerche sugli ellissoidi rotanti furono intraprese nel 1740 da Colin Maclaurin che prese in considerazione un caso particolare di ellissoidi di rotazione, studiato poi in maggior dettaglio da Laplace. Il caso generale di ellissoidi triassiali fu analizzato nel 1834 da Carl Gustav Jacob Jacobi e nel 1842 fu scoperta da Oskar Emil Meyer una famiglia degli ellissoidi triassiali a un solo parametro, vicini agli ellissoidi di Maclaurin, con eccentricità meridiana pari a 0,813. Le ricerche sulle forme di equilibrio ad anello, iniziate già da Laplace negli anni Ottanta del Settecento, furono estese anche al moto dei due corpi (stelle doppie). Tra il 1860 e il 1861 Dirichlet, Richard Dedekind e Georg Friedrich Bernhard Riemann studiarono (in variabili lagrangiane) figure di equilibrio di forma ellissoidale variabile.

La questione più difficile inerente alla stabilità delle figure di equilibrio fu sollevata da Joseph Liouville e da Riemann. Il progresso decisivo fu opera di Aleksandr Michajlovič Ljapunov (1857-1918) e Jules-Henri Poincaré (1854-1912), i quali presentarono metodi piuttosto generali per studiare le figure di equilibrio di un fluido rotante, inclusa la loro stabilità secolare. Le prime ricerche di entrambi gli scienziati in questo campo risalgono alla metà degli anni Ottanta. Già nella sua tesi del 1884, Ljapunov aveva dimostrato la stabilità degli ellissoidi di Maclaurin con valori di eccentricità minori di 0,813, sotto ipotesi generali relative ai disturbi, e la stabilità degli ellissoidi di Jacobi sotto disturbi ellissoidali. Successivamente gli ellissoidi di biforcazione furono sottoposti ad accurata indagine e, in particolare, furono scoperte le cosiddette figure di equilibrio 'a forma di pera'. Nel 1905 Ljapunov dimostrò l'instabilità di queste forme, contraddicendo le affermazioni di Darwin sulla loro stabilità. Questo disaccordo provocò una discussione che si concluse ben presto in favore di Ljapunov, che intraprese ricerche fondamentali sulle figure di equilibrio dei fluidi rotanti omogenei ed eterogenei.

Flussi a getto e onde superficiali

Risultati di grande rilievo furono ottenuti nel corso del XIX sec. nel campo dell'analisi dei flussi potenziali stazionari piani di un fluido incomprimibile. Il concetto di funzione di corrente per un flusso piano fu introdotto da Lagrange (1781-1783), mentre la sua interpretazione cinematica fu fornita nel 1864 da William J.M. Rankine. La funzione di corrente nei flussi irrotazionali, così come il potenziale di velocità, soddisfa l'equazione di Laplace. Il successo della teoria delle funzioni di una variabile complessa portò all'impiego dei suoi metodi di analisi nei problemi piani del moto di un fluido incomprimibile, sviluppatisi parallelamente a quelli di elettrostatica. I primi lavori, nei quali i problemi elementari di elettrostatica e idrodinamica venivano studiati con l'aiuto della teoria delle funzioni analitiche, risalgono agli anni Sessanta dell'Ottocento. Lo sviluppo fondamentale, relativo alle applicazioni della teoria delle funzioni in idrodinamica, è legato allo studio di una classe particolare di moti fluidi, inaugurato nel 1868 da Helmholtz, che riguarda i cosiddetti 'flussi a getto', dotati di linee di corrente libere sulle quali agisce una pressione costante. L'interesse per questi flussi sorse in relazione ai tentativi di ottenere, sulla base del modello di un fluido ideale, immagini realistiche del flusso attorno ai solidi, generato da una forza di trascinamento senza velocità infinite.

La soluzione del problema del flusso a getto in uscita dall'imboccatura di Borda venne fornita da Helmholtz stesso. Nel 1869 Kirchhoff propose il primo metodo generale per risolvere problemi per un getto piano, basati sulla costruzione della funzione

[22] ζ=∂z/∂w,

dove w=φ+iψ è il potenziale complesso di flusso. La costruzione della soluzione w=w(z) viene poi ottenuta invertendo la relazione

[23]  z=∫ζ(w)dw.

Kirchhoff fornì soluzioni per un flusso a getto dietro a una piastra e per l'uscita da un orifizio. In particolare, per il fattore di compressione di un getto egli ottenne il valore π/(π+2)≈0,611, vicino al valore sperimentale di 0,62. L'applicazione del metodo di Kirchhoff ad altri problemi fu successivamente effettuata da Rayleigh, Moritz Réthy, Bobylev, Voigt, Aleksandr Petrovič Kotelnikov e altri.

Un importante contributo fu introdotto nella teoria dei flussi a getto contemporaneamente da Žukovskij e John H. Michell nel 1890, i quali proposero modifiche efficaci del metodo di Kirchhoff, basato sulla costruzione delle funzioni w(t) e

[24]  Ω=logdz/dw=-logV+iθ=Ω(t),

che connettono i domini di flusso sui piani w e Ω con un certo dominio su un piano ausiliario della variabile complessa t. Nel piano della funzione Ω, flussi a getto univalenti con contorni rettilinei sono rappresentati da poligoni univalenti. Un ampio uso della funzione Ω e l'introduzione di una variabile ausiliaria parametrica (Žukovskij e Michell considerarono un semipiano per il dominio di flusso sul piano della variabile complessa ausiliaria) hanno permesso di ampliare in modo sostanziale il gruppo di problemi risolti della teoria del getto. Il processo di costruzione delle funzioni w(t) e Ω(t) fu condotto da Žukovskij con l'ausilio di una procedura ad hoc (fondamentalmente vicina al metodo di Čaplygin dei punti singolari) che egli accompagnò con un'elegante interpretazione geometrica; per ottenere la soluzione, Michell utilizzò direttamente la formula di Schwarz-Christoffel.

Grazie ai lavori di Žukovskij, Michell, Love e altri, il numero di problemi risolti per la teoria dei getti crebbe in maniera notevole. Alle ricerche del 1890 di Pieter Molenbroek sui primi problemi sul flusso potenziale dei getti gassosi fece seguito una soluzione generale apparsa nella celebre tesi di dottorato di Čaplygin del 1902.

Un certo numero di lavori fu dedicato nel corso del XIX sec. alla teoria delle onde. Questa parte fondamentale dell'idrodinamica di un flusso ideale si distinse per il fatto che diede risultati che si accordavano sostanzialmente con i dati sperimentali e d'osservazione. Negli anni 1815 e 1816 Cauchy e Poisson posero le prime basi della teoria delle piccole onde superficiali di un fluido grazie al promettente metodo della linearizzazione delle condizioni al contorno (mediante il loro trasferimento sulla superficie non perturbata). Da allora la teoria delle onde di Cauchy-Poisson è stata sviluppata con successo e applicata in pratica. Senza entrare nei dettagli, sarà sufficiente ricordare inoltre un ampio gruppo di ricerche sulla propagazione delle maree, opera soprattutto della scuola inglese (Airy, Stokes, Thomson, Rayleigh, Darwin, Lamb).

Idrodinamica dei gas: onde d'urto

In origine la comprimibilità dei fluidi era presa in considerazione nelle ricerche teoriche solo quando si studiava la propagazione del suono. La prima formula per la velocità del suono fu offerta da Newton e corrisponde al processo isotermo ideale di propagazione delle onde acustiche. Il carattere adiabatico della propagazione del suono fu stabilito da Laplace nei primissimi anni del XIX sec., ma egli pubblicò i suoi risultati soltanto nel 1817, dando, per la velocità di propagazione del suono a, la formula (in notazione moderna)

dove c_p e cν sono, rispettivamente, il calore specifico a pressione e volume costanti.

L'introduzione della dipendenza esplicita della pressione dalla densità per processi adiabatici p:p₀=ϱ^k:ϱ^k₀, che successivamente ha ricevuto il nome di curva adiabatica di Poisson, risale anch'essa allo stesso periodo. Una generalizzazione della formula di Laplace, per qualunque tipo di dipendenza p(ϱ), venne sviluppata soltanto durante gli anni Ottanta dell'Ottocento.

L'analisi della propagazione del suono nell'aria ebbe inizio nel corso del XVIII sec., grazie a Euler e Lagrange. In un lavoro di Euler si trova l'equazione delle fluttuazioni acustiche

Un contributo essenziale allo sviluppo di metodi matematici per l'analisi della propagazione delle onde sonore fu fornito nel corso degli anni Venti dell'Ottocento da Poisson e, nella seconda metà del secolo, dalla scuola inglese (Stokes, Rayleigh, Lamb).

Un interesse teorico per lo studio dei processi delle onde nei gas portò, verso la metà del XIX sec., alla scoperta delle onde d'urto. Il disturbo della simmetria delle onde acustiche di larga ampiezza fu notato nel 1851 da Stokes, il quale s'impegnò per la prima volta anche in considerazioni sulle discontinuità di densità in un flusso. Nel 1860 Samuel Earnshaw aveva cominciato ad affrontare lo studio di equazioni di discontinuità, ma la prima dimostrazione matematica della possibilità di generare discontinuità in un flusso gassoso si deve a Riemann che nello stesso anno scoprì l'esistenza di due famiglie di curve (invarianti di Riemann) e impiegò condizioni di conservazione della massa e della quantità di moto su una discontinuità. Tuttavia Riemann commise un errore accettando la dipendenza adiabatica p(ϱ) per un gas che oltrepassa un'onda d'urto, e questo ebbe come effetto una violazione della condizione di conservazione dell'energia in corrispondenza della discontinuità.

Un approccio termodinamico piuttosto rigoroso (sebbene non molto ben formulato) per lo studio delle onde d'urto fu sviluppato nel 1870 da Rankine, il quale derivò una soluzione abbastanza completa del problema delle discontinuità. Il suo lavoro, tuttavia, non include alcune importanti conseguenze che, in effetti, discendono dai suoi ragionamenti e dalle sue equazioni. Così, per esempio, egli fa riferimento a un'osservazione di Thomson sull'instabilità di un'onda di rarefazione e non nota che, dalla condizione che egli impone sul bilancio di calore in un'onda d'urto, mediante un ovvio ragionamento di tipo termodinamico, si può dedurre che è impossibile che esistano onde d'urto di rarefazione ‒ un fatto che fu riconosciuto solo negli anni 1904-1905 da G. Zemplén.

Il passo successivo nello studio delle onde d'urto fu compiuto nel 1887 da Pierre-Henri Hugoniot, il quale studiò le onde d'urto mediante l'uso diretto delle tre equazioni di conservazione in corrispondenza della discontinuità. Egli ottenne così la relazione tra le pressioni e le densità prima e dopo la discontinuità

dove ϰ=c_p/cν, oggi nota come 'relazione adiabatica di Hugoniot'. È interessante notare che la relazione corrispondente tra le velocità fu trovata solamente nel 1910 da Prandtl.

Un'analisi puramente matematica sulla possibile esistenza di superfici di discontinuità nel flusso di un fluido compresso fu sviluppata contemporaneamente e furono studiati i salti generali di ordine n-esimo corrispondenti alla discontinuità di una delle derivate dⁿx_i/daⁿ_i (dove x_i e a_i sono le coordinate finali e iniziali delle particelle del fluido), sotto la condizione di continuità delle derivate di ordine inferiore. Alcuni risultati furono ottenuti da Elwin Bruno Christoffel nel 1877 e da Hugoniot nel 1885; tuttavia l'analisi generale del problema fu sviluppata da Jacques Hadamard tra il 1901 e il 1903.

Grazie a ricerche che si protrassero per mezzo secolo, la teoria delle onde d'urto sembrava ormai definita in modo piuttosto dettagliato, anche se il suo oggetto rimase, fondamentalmente, di tipo abbastanza speculativo. Lo sviluppo di tecniche che permettessero lo studio sperimentale effettivo delle onde d'urto fu compito del XX secolo. È necessario ricordare soltanto gli esperimenti di Ernst Mach (1838-1916), il quale, alla fine degli anni Ottanta dell'Ottocento, scattò alcune foto perfette (per la tecnica del tempo) di onde d'urto in flussi supersonici di gas attraverso corpi. Per queste ricerche, il cono dell'onda d'urto fu battezzato con il suo nome e, successivamente, anche il parametro adimensionale fondamentale, il rapporto tra la velocità di flusso e quella del suono (il 'numero di Mach', appunto).

Lo studio del flusso di un gas secondo un'esposizione (quasi monodimensionale) di tipo idraulico ebbe origine dal lavoro di Navier nel quale sviluppava una formula per la velocità di uscita di un gas da un orifizio applicabile nel caso di piccole differenze di pressione (i primi tentativi elementari di calcolare il flusso di uscita di un gas mediante una trattazione quasi monodimensionale risalgono alla metà del XVIII sec.; si veda l'Hydrodynamica (1738) di Daniel Bernoulli). Alla fine degli anni Trenta dell'Ottocento Saint-Venant e Pierre-Laurent Wantzel (1814-1848) svilupparono una generalizzazione di questa formula per grandi differenze di pressione e realizzarono numerosi esperimenti per la definizione dei limiti della sua applicabilità. Un'analisi dei problemi legati al flusso d'uscita non stazionario fu affrontata in origine da Julien-Napoléon Haton de la Goupillière (1833-1927) e, successivamente, con una trattazione più rigorosa, da Hugoniot.

Accanto ad aspetti puramente idrodinamici del moto dei gas, nella seconda metà del XIX sec. furono studiati alcuni processi chimico-fisici nei gas. Si citano a titolo d'esempio i lavori sulla teoria della diffusione e del mescolamento dei gas condotti intorno al 1870 da Josef Stefan (1835-1893). L'inizio delle analisi dei gas combusti risale all'ultimo decennio dell'Ottocento: Vladimir A. Michelson diede inizio nel 1890 alla teoria della combustione lenta e David L. Chapman prese in considerazione i processi di detonazione (1899) scoprendo l'onda di detonazione, poi studiata in dettaglio all'inizio del XX sec. da Émile Jouguet e chiamata successivamente onda di Chapman-Jouguet.

Per concludere, è necessario menzionare l'origine, nel corso del XIX sec., della teoria cinetica dei gas, rivelatasi estremamente importante per i successivi sviluppi della dinamica dei gas rarefatti. Considerazioni elementari sulla teoria cinetica dei gas risalgono ai lavori effettuati da Jacob Hermann e Daniel Bernoulli nella prima metà del XVIII secolo. Un vivace interesse per questi problemi rinacque nella prima metà del XIX sec. con John Herapath, James P. Joule, August Karl Krönig, Rudolf Clausius e altri. Infine, la teoria cinetica dei gas si sviluppò seriamente in senso statistico nei lavori di Maxwell dal 1860 in poi, per raggiungere una certa completezza in quelli di Ludwig Boltzmann alla fine del secolo. Diversamente dalla meccanica, che nel XIX sec. era considerata essenzialmente matematica applicata, la teoria cinetica dei gas incontrò notevoli ostacoli di carattere interno ed esterno: basata sul concetto fenomenologico di atomi, ebbe per lungo tempo nemici irriducibili che non erano disposti a riconoscere i suoi successi. A tal proposito si ricordano le parole dell'anziano fisico sperimentale Gustave Adolphe Hirn, il quale definì la teoria cinetica dei gas come "uno degli errori più disastrosi della scienza moderna".

La resistenza idraulica nel moto dei fluidi

L'ingegneria idraulica, come parte della meccanica dei fluidi, si trovava nel corso del XIX sec. in una situazione piuttosto originale. I lavori che riguardavano le forniture d'acqua, l'impiego dell'energia dell'acqua, così come la costruzione di canali e strutture di ingegneria idraulica avevano bisogno di analisi sempre più precise del flusso dell'acqua nei tubi, in canali aperti e in varie apparecchiature speciali. Tuttavia, l'idrodinamica teorica non diede nessuna risposta ai vari problemi che andavano ponendosi, così come non fu in grado di spiegare il fenomeno fondamentale che è inerente a tutti i sistemi pratici: la resistenza idraulica. Nel corso del XIX sec. il compito principale dell'idraulica fu pertanto lo studio sperimentale della resistenza idraulica in diverse condizioni. Come successivo compito teorico in questo periodo si può considerare l'applicazione dei teoremi generali della meccanica all'analisi del flusso dell'acqua, principalmente in canali aperti, operando con medie delle velocità sulle sezioni trasversali di flusso.

All'inizio del XIX sec. l'idraulica aveva già raccolto, grazie soprattutto alla scuola francese, dati sul valore della resistenza idraulica per un flusso d'acqua uniforme. Le indagini di Antoine de Chézy (1718-1798) sul flusso nei canali risalgono agli anni Settanta del XVIII sec., tuttavia i risultati delle sue ricerche non furono pubblicati immediatamente. Partendo dalla legge quadratica della resistenza, egli scoprì che le velocità medie del flusso in un canale sono proporzionali alla radice quadrata del prodotto tra la pendenza del letto del canale e il rapporto tra il flusso sulla sezione trasversale e il suo perimetro bagnato ‒ che costituisce la cosiddetta 'formula di Chézy'. Agli stessi anni risale anche l'edizione delle monografie sull'idraulica di Charles Bossut e Pierre-Louis-Georges Du Buat, edizione che segnò l'inizio di una lunga serie di pubblicazioni di idraulica. Nel periodo compreso tra il 1800 e il 1804 fu pubblicato un certo numero di lavori (Coulomb, Eytelwein, Gaspard-François-Clair-Marie Riche de Prony e altri) nei quali furono sviluppate formule per la resistenza idraulica come quella di Chézy e formule a due termini del tipo I=aU+bU² (in una memoria di Prony già si incontrano i simboli familiari U, χ e ω per la velocità media, il perimetro bagnato e la sezione trasversale di flusso). Gli ulteriori successi nell'analisi della resistenza idraulica sono legati alle accurate ricerche (1839-1855) di Hagen, già menzionate, in cui viene indagata l'influenza di diversi fattori, in particolare della temperatura, sul flusso dell'acqua. A metà dell'Ottocento l'ingegnere tedesco Julius Ludwig Weisbach (1806-1871), autore dell'opera edita più volte Lehrbuch der Ingenieur- und Maschinen-Mechanik (Trattato di ingegneria e meccanica delle macchine, 1845-1860), diede una forma abbastanza moderna alla progettazione idraulica delle tubazioni, relativamente al problema delle perdite locali. Il suo nome è stato attribuito alla formula per le perdite di pressione nel flusso dei fluidi nelle tubazioni.

Le ricerche pratiche più significative sulla resistenza idraulica di canali e tubi furono condotte da Darcy e dal suo collaboratore Henri-Émile Bazin a metà del XIX secolo. La maggior parte delle formule empiriche note per le perdite idrauliche, che sono ancora oggi utilizzate, risalgono alla seconda metà del secolo: le formule di Gauckler (1868), Ganguillet-Kutter (1869), Manning (1889) e quella modificata di Bazin (1897). Quest'ultima include già esplicitamente la rugosità delle pareti delle condotte. Ulteriori progressi, fondamentali nello studio della resistenza idraulica, furono possibili soltanto in seguito all'introduzione dell'analisi dimensionale nella pratica ingegneristica, avvenuta nel primo quarto del XX sec., e dopo la creazione di teorie semiempiriche per la turbolenza verificatasi negli anni Trenta del Novecento (Prandtl, Kármán e altri).

Nel XIX sec. furono sviluppate le basi per il progetto relativo ai flussi d'acqua non uniformi gradualmente variati in canali aperti. Nel XVIII sec. era stata fornita, relativamente al problema dei flussi dell'acqua a superficie libera, solamente la formula per il flusso attraverso gli sfioratori (elaborata da Giovanni Poleni nel 1717). La deduzione di un'equazione differenziale elementare del flusso stazionario non uniforme in canali rettangolari apparve per la prima volta, a quanto sembra, nell'opuscolo pubblicato anonimo da Giuseppe Venturoli (1768-1846). Una rinascita di interesse per i problemi del flusso non uniforme nei canali aperti si verificò dopo una nuova derivazione delle equazioni del flusso, fornita da Jean-Baptiste-Charles-Joseph Bélanger (1828) e discussa da P. Vothier (1836). L'analisi delle superfici libere d'acqua in canali aperti fu elaborata nei lavori di Dupuit (1848) e Saint-Venant (1850-1851). Finalmente Jacques-Antoine-Charles Bresse (1860) integrò l'equazione di un flusso non uniforme per canali larghi e preparò tabelle ausiliarie per il progetto delle curve di accumulo e svuotamento d'acqua. L'ulteriore sviluppo nel calcolo del flusso non uniforme in qualunque canale prismatico fu opera, nel XX sec., di Boris Aleksandrovič Bachmetev (1912), che introdusse la cosiddetta 'energia specifica di sezione trasversale'.

Parallelamente al progetto generale del flusso non uniforme in canali aperti, venne investigato il fenomeno del salto idraulico: la sua analisi fu iniziata negli anni Venti dell'Ottocento a opera di Giovanni Giorgio Bidone e Bélanger e fu completata da Bresse. Bélanger introdusse anche il principio di scarico massimo per lo stramazzo in parete spessa (1849). L'idraulica dei fiumi richiese anche lo studio del processo di deformazione del letto e, in particolare, del moto del sedimento. Al 1879 risale la memoria di P.F. Du Boys in cui studiò la forza di trascinamento di un flusso e diede la prima formula per lo scarico di un sedimento in un flusso.

Le equazioni del moto non stazionario dell'acqua in canali aperti furono dedotte per la prima volta da Saint-Venant nel 1871. Si tratta di equazioni iperboliche i cui integrali particolari, nel caso di resistenza idraulica nulla, furono trovati dallo stesso Saint-Venant, sebbene i metodi generali per la loro integrazione richiedessero un'applicazione del metodo delle caratteristiche. Tale metodo è stato in qualche modo sviluppato alla fine del XIX sec. nei lavori del matematico belga Junius Massau (1899). Un'analisi generale dei problemi idraulici del moto dell'acqua in canali aperti, sotto molti aspetti ancora oggi insuperata, fu fornita da Boussinesq nel suo trattato già menzionato.

Un altro importante problema pratico relativo al moto non stazionario dell'acqua, ossia il 'colpo d'ariete' in tubazioni elastiche, sotto condizioni di controllo dello scarico d'acqua, è stato risolto alla fine del secolo. Le prime ricerche teoriche del flusso non stazionario in tubazioni sembrano essere state intraprese nel corso degli anni Ottanta del XIX sec. da Gromeka, ma il problema pratico del 'colpo d'ariete' attirò l'attenzione di Žukovskij soltanto negli ultimi anni del secolo, in seguito al progetto di ricostruzione dell'acquedotto di Mosca. Nel 1898 egli trovò la velocità di propagazione delle onde di pressione nelle tubazioni, problema che sarà ulteriormente studiato e approfondito da Lorenzo Allievi all'inizio del XX secolo.

In questo capitolo non sono state trattate le tecniche sperimentali di idrodinamica e idraulica. È necessario notare tuttavia che, se all'inizio del XIX sec. gli sperimentatori disponevano perlopiù di piccole installazioni da camera con piccoli canali artificiali, tubi di Pitot e misuratori di corrente di Woltmann, alla fine del secolo potevano già utilizzare grandi laboratori di ricerca specializzati dotati di molte apparecchiature, tra cui enormi vasche di prova.

Bibliografia

Benvenuto 1991: Benvenuto, Edoardo, An introduction to the history of structural mechanics, New York, Springer, 1991, 2 v. (ed. orig.: La scienza delle costruzioni e il suo sviluppo storico, Firenze, Sansoni, 1981).

Born 1915: Born, Max, Dynamik der Kristallgitter, mit einer tafel und 2 figuren im text, Leipzig und Berlin, Teubner, 1915.

Darrigol 2002: Darrigol, Olivier, Between hydrodynamics and elasticity theory. The first five births of the Navier-Stokes equation, "Archive of history for exact sciences", 56, 2002, pp. 95-150.

Dugas 1950: Dugas, René, Histoire de la méchanique, Neuchâtel, Éditions du Griffon, 1950.

Garbrecht 1987: Hydraulics and hydraulic research. A historical review, edited by Günther Garbrecht, Rotterdam-Boston, Balkema, 1987.

Grattan-Guinness 1981: Grattan-Guinness, Ivor, Essay review. Recent researches in French mathematical physics of the early 19th century, "Annals of sciences", 38, 1981, pp. 663-690.

‒ 1984: Grattan-Guinness, Ivor, Work for the workers. Advances in engineering mechanics and instruction in France, 1800-1830, "Annals of science", 41, 1984, pp. 1-33.

Hager 1990: Hager, Willi H., Geschichte des Wassersprungs, "Schweizer Ingenieur und Architekt", 25, 1990, pp. 728-735.

‒ 1994: Hager, Willi H., Die historische Entwicklung der Fliessformel, "Schweizer Ingenieur und Architekt", 9, 1994, pp. 123-133.

Klein 1901-14: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. IV/3: Mechanik der deformierbaren Körper. Analytisch-geometrische Hilfsmittel, Hydrodynamik, redigiert von Felix Klein und Conrad Müller, 1901-1908; v. IV/4: Mechanik der deformierbaren Körper. Elastizität und Festigkeitslehre, redigiert von Felix Klein und Conrad Müller, 1907-1914.

Mahrenholtz 1978: Mahrenholtz, Oskar - Gaul, Lothar, Die Mechanik im 19. Jahrhundert, "Zeitschrift der Technischen Universität Hannover", 5, 1978, pp. 28-48.

Rouse 1957: Rouse, Hunter - Ince, Simon, History of hydraulics, Iowa City, State University of Iowa Press, 1957 (rist.: New York, Dover, 1963).

Szabó 1977: Szabó, István, Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, Basel, Birkhäuser, 1977 (2. ed.: 1979; 3. ed.: 1987).

Timoshenko 1953: Timoshenko, Stephen P., History of strength of materials, with a brief account of the history of theory of elasticity and theory of structures, New York, McGraw Hill, 1953.

Truesdell 1968: Truesdell, Clifford A., Essays in the history of mechanics, Berlin-Heidelberg-New York, Springer, 1968.

Ziegler 1985: Ziegler, Renatus, Die Geschichte der geometrischen Mechanik im 19. Jahrhundert. Eine historisch-systematische Untersuchung von Möbius und Plücker bis zu Klein und Lindemann, Stuttgart, Steiner, 1985.