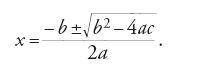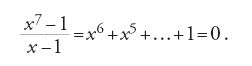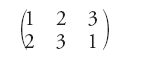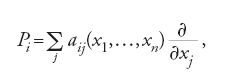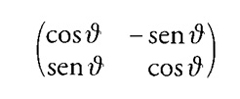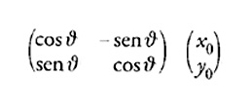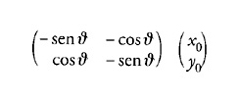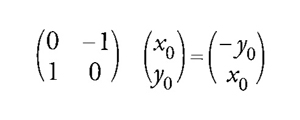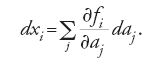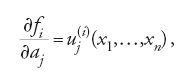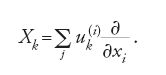L'Ottocento: matematica. Le origini della teoria dei gruppi

L'Ottocento: matematica. Le origini della teoria dei gruppi

Le origini della teoria dei gruppi

La teoria di Galois e la soluzione algebrica delle equazioni algebriche

La teoria di Galois risponde al quesito: quando un'equazione algebrica è risolubile per radicali? Per comprendere cosa questo significhi e perché sia importante, si consideri un'equazione di secondo grado della forma ax²+bx+c=0. Essa è risolubile estraendo due radici quadrate e le sue soluzioni sono date dalla ben nota formula

Le soluzioni sono pertanto espresse in funzione dei coefficienti del polinomio (il primo membro dell'equazione stessa), utilizzando le quattro operazioni elementari dell'aritmetica e l'operazione di estrazione di radice, in questo caso di radice quadrata. La grande conquista dei matematici italiani dell'inizio del XVI sec. fu la definizione di una formula simile per le equazioni di terzo grado (o 'cubiche'), nella quale compaiono sia radici cubiche sia radici quadrate, e una formula più complessa per le equazioni di quarto grado (dette anche 'quartiche').

Agli inizi del XIX sec. nessun matematico era riuscito a trovare una formula per la risoluzione delle equazioni di quinto grado (le 'quintiche'). Nel 1770 Joseph-Louis Lagrange aveva cominciato a sviluppare una teoria in grado di spiegare le ragioni di questo insuccesso, ma non l'aveva condotta a termine. I suoi metodi erano stati portati a un passo dalla conclusione anche dall'italiano Paolo Ruffini (1765-1822), nel 1799. Nelle sue argomentazioni, tuttavia, permaneva una lacuna, peraltro considerata dalle generazioni successive reale ma modesta, cosicché i suoi contemporanei si erano rifiutati di accettarle. Ruffini aveva riprovato nuovamente nel 1806 e nel 1813. I suoi lavori avevano ottenuto una vaga approvazione da parte della Royal Society di Londra e il cauto parere di Lagrange secondo il quale tali lavori, per quanto validi, non offrivano una trattazione esauriente della materia.

Per contro, i metodi sviluppati da Lagrange riscossero un largo successo negli anni Venti del XIX sec. grazie al lavoro di Niels Henrik Abel, il quale aveva dimostrato che per una generica equazione di quinto grado non esiste una formula risolutiva che utilizzi solamente le quattro operazioni elementari e l'estrazione di radice.

Il lavoro di Abel conteneva anche l'osservazione che un'equazione di quinto grado risolubile per radicali ha una forma speciale, differente da quella propria di una generica equazione dello stesso grado. La natura di tale forma si comprende analizzando come i coefficienti del polinomio si possano esprimere in funzione delle radici e, in particolare, individuando le necessarie proprietà di simmetria che gli stessi coefficienti devono avere quando le radici vengano sottoposte a permutazione. Il problema è reso più complesso dal fatto che, nel corso di un procedimento che porti alla soluzione di una equazione di quinto grado, è lecito aspettarsi di dover risolvere molte altre equazioni più semplici.

Ciò sembra suggerire che un'equazione algebrica è risolubile per radicali se e solo se ha grado minore o uguale a quattro. D'altra parte, come Abel ben sapeva, esistono equazioni di grado più elevato risolubili per radicali. È il caso, per esempio, di questa equazione di sesto grado:

Le radici della [2] sono le sei radici settime 'non banali' dell'unità (ossia i sei numeri complessi, diversi dall'unità, che elevati alla settima potenza sono uguali a uno). Per determinarle algebricamente si può dividere l'equazione [2] per x³, ottenendo così x³+x²+x+1+x⁻¹+x⁻²+x⁻³=0. Posto allora x+x⁻¹=u, si è ricondotti a risolvere l'equazione u³+u²−2u−1=0, che è di terzo grado in u. Noto un valore di u, i corrispondenti valori di x si determinano risolvendo l'equazione quadratica x²−ux+1=0; pertanto, si può concludere che l'equazione [2] è risolubile per radicali. Questo significa che l'individuazione delle equazioni algebriche risolubili per radicali richiede un'analisi più raffinata, che non tenga conto soltanto del grado del polinomio a primo membro.

La teoria di Galois spiega la natura del problema, consentendo di rispondere ad altri interessanti interrogativi, quali per esempio: quando (sotto quali condizioni) le soluzioni di una equazione algebrica (di grado superiore al quarto) possono ottenersi mediante estrazione di radici quadrate? Questo antico problema era stato riformulato da Carl Friedrich Gauss nelle Disquisitiones arithmeticae, in riferimento alla costruzione con riga e compasso di un poligono regolare di n lati. Si tratta di risolvere l'equazione, di grado n−1, (xⁿ−1)/(x−1)=0, che Gauss dimostra essere risolubile con l'uso delle quattro operazioni e l'estrazione di radici quadrate se e solo se n è della forma 2^k+1, per valori di k che sono potenze di 2.

Altri esempi vengono da un ramo della matematica più difficile, ma più importante, della teoria delle costruzioni con riga e compasso: la teoria delle funzioni ellittiche. In quest'ambito Carl Gustav Jacob Jacobi ha individuato una classe di equazioni (le 'equazioni modulari') che risultano inaspettatamente riducibili. Senza entrare nei dettagli (che ci condurrebbero troppo lontano), Jacobi trova un'equazione polinomiale di grado 5 che si può ridurre con manipolazioni algebriche a un'equazione di grado 4, una di grado 7 che si può ridurre a una di grado 6 e, infine, una di grado 11 che si può ridurre a una di grado 10. Tale scoperta suscitò l'attenzione di Galois.

Galois fu in grado di dimostrare che un'analoga riduzione non può aver luogo per equazioni di grado superiore a 11, fornendo altresì una risposta completa al quesito: sotto quali condizioni un'equazione algebrica è risolubile per radicali? Dati due numeri a e b, trovare la radice n-esima di a/b equivale a risolvere l'equazione binomie bxⁿ−a=0; pertanto, risolvere un'equazione per radicali significa risolvere una successione di equazioni binomie. Ci si chiede allora quando sia possibile individuare equazioni binomie ad hoc. Si possono considerare equazioni binomiali a coefficienti razionali, risolvendo le quali si ottengono altri numeri da assumersi poi come noti. Si possono formare equazioni binomie ad hoc, e in caso affermativo, quali?

Adottando la terminologia moderna, si può descrivere il ragionamento di Galois nel modo seguente. Sia data un'equazione algebrica di grado n, le cui n radici siano distinte. Le permutazioni di tali radici formano un gruppo di ordine al più n!, e si possono scrivere polinomi di grado n per i quali il gruppo di permutazioni delle radici coincide con il gruppo delle permutazioni di n lettere. Tuttavia un'equazione della forma xⁿ+b=0 ha come soluzioni la radice reale n-esima di −b moltiplicata per le radici complesse n-esime dell'unità. Se è noto l'effetto della permutazione su una di queste radici, allora è noto l'effetto su tutte le altre (che si ottengono come potenze di quella); in questo caso, pertanto, le possibili permutazioni delle radici formano un sottogruppo ciclico di ordine n. L'intuizione di Galois fu che le equazioni risolubili per radicali sono quelle il cui gruppo si ottiene, in qualche modo, come successione di questi sottogruppi ciclici.

Il lavoro di Galois va ritenuto originale non soltanto perché egli fu uno dei primi a far ricorso al concetto di gruppo ‒ peraltro, inteso in un senso leggermente diverso da quello che il termine ha oggi assunto e che pure deriva dal suo stesso lavoro ‒ ma soprattutto perché le sue argomentazioni evidenziano anche l'importanza, precedentemente mai considerata, di analizzare il modo in cui un gruppo può essere sottogruppo di un altro. In effetti, il punto chiave dell'analisi di Galois consiste nella definizione del concetto di sottogruppo normale, il quale gioca un ruolo essenziale nel determinare come un gruppo possa essere costituito da una successione di sottogruppi.

Galois introdusse un linguaggio completamente nuovo nell'analisi della risolubilità di equazioni per radicali. Da quel momento in poi fu possibile discutere l'argomento in funzione sia del gruppo associato a un'equazione sia della sua decomponibilità o meno in una successione di gruppi ciclici. Galois ha anche indicato che per ottenere una tale decomposizione occorre considerare sottogruppi normali.

Il fatto che certe equazioni modulari si riducano a equazioni di grado inferiore si spiegava con il fatto che i gruppi a loro associati sono anche gruppi di equazioni di grado inferiore. Se poi le radici di un'equazione sono costruibili con riga e compasso, ciò si spiegava con l'essere il suo gruppo composto da una successione di sottogruppi di ordine due. Infine, il fatto che l'equazione generale di quinto grado non sia risolubile per radicali, è conseguenza diretta, secondo l'analisi di Galois, dell'essere il suo gruppo (il gruppo completo delle permutazioni di 5 lettere) non decomponibile in una successione di sottogruppi ciclici.

Più precisamente e adottando la terminologia moderna, Galois introduce il concetto di 'sottogruppo normale' N di un gruppo G. Un sottogruppo N di un gruppo G è normale se e solo se per ogni elemento n∈N e per ogni elemento g∈G, risulta g⁻¹ng∈N. Questo significa che, assunta come regola di moltiplicazione fra classi laterali g₁Ng₂N=g₁g₂N, le classi laterali gN di N in G, ossia l'insieme degli elementi gn, con n∈N, formano esse stesse un gruppo. Questo gruppo si dice 'gruppo quoziente di G modulo N' e si indica con G/N. Un gruppo è risolubile se e solo se ammette una catena di sottogruppi G_i, con 1≤i≤k, dove: G₁ è il gruppo costituito dal solo elemento unità di G, G_k=G, ogni G_i è normale in G_i+1 e ogni gruppo quoziente G_i+1/G_i è un gruppo ciclico. Galois applica queste definizioni alla teoria delle equazioni algebriche, studiando il gruppo G delle permutazioni delle radici di un'equazione. Egli considera un'equazione a coefficienti razionali e giunge alla conclusione che essa è risolubile per radicali se le radici possono essere ottenute mediante la progressiva aggiunta di espressioni dipendenti solamente dalle radici di quantità note. La progressiva decomposizione di G in una catena di sottogruppi normali, aventi quozienti ciclici, corrisponde alla progressiva aggiunta di tali radici.

Sarebbe difficile sottovalutare la portata delle innovazioni introdotte dall'analisi e dalle conclusioni di Galois nella teoria delle equazioni algebriche, innovazioni che possono così sintetizzarsi: occorre studiare non le equazioni, ma oggetti molto più astratti ‒ i gruppi associati alle equazioni ‒ i quali vanno analizzati con i metodi della (nuova) 'teoria dei gruppi'.

Sarebbe stato già notevole che questo punto di vista fosse stato proposto da un matematico maturo. È addirittura stupefacente che si tratti invece della creazione di un uomo che morì all'età di vent'anni, ferito mortalmente in un duello. La sua è senz'altro la più drammatica fra le biografie dei matematici. Evariste Galois nacque il 25 ottobre 1811 in un sobborgo di Parigi e fu educato nel College Royal Louis-le-Grand, dove il suo maestro Hippolyte-Jean Vernier lo introdusse seriamente alla matematica quando era quindicenne. Egli lesse le Réflexions sur la résolution algébrique des équations di Lagrange e nella classe superiore del College Royal Louis-le-Grand ebbe come insegnante Louis-Paul-Émile Richard, il quale riconobbe immediatamente il talento di Galois e lo incoraggiò a pubblicare il suo primo articolo sulla teoria dei numeri nelle "Annales de mathematiques" di Gergonne (aprile 1828). Il 25 maggio e il 1° giugno 1829 Galois presentò due articoli all'Académie des Sciences sulla risolubilità delle equazioni di grado dato da un numero primo. Si tratta dei primi lavori sulla 'teoria di Galois' e Augustin-Louis Cauchy venne invitato a riferire su essi. Per ragioni che rimangono oscure, Galois non superò l'esame di ammissione all'École Polytechnique per ben due volte e quindi si iscrisse all'École Normale Supérieure nel novembre del 1829. In seguito Cauchy trascurò di riferire sul lavoro di Galois, presumibilmente convinto che Galois avrebbe riscritto i suoi lavori per partecipare al premio per la matematica, bandito dall'Académie che scadeva il 1° marzo 1830. Galois presentò il suo manoscritto in febbraio, ma in maggio il segretario permanente dell'Académie e presidente della commissione giudicatrice, Fourier, morì e il lavoro di Galois andò smarrito. Galois denunciò allora l'esistenza di quello che egli riteneva un complotto accademico ordito contro di lui per motivi politici e si schierò risolutamente tra le fila della sinistra più radicale.

Il 1830 fu in Francia un anno rivoluzionario e quando Carlo X nel mese di luglio, dopo tre giorni di rivolte a Parigi, fuggì dalla Francia, il regime borbonico cadde. Al suo posto si insediò il re, Luigi Filippo d'Orléans e, con una decisione al limite del ridicolo, in settembre Cauchy seguì volontariamente Carlo X in esilio. Galois si schierò con i rivoluzionari Blanqui e Raspail e prima della fine dell'anno fu espulso dall'École Normale. Per tutto il 1831 Galois fu assorbito dalla politica rivoluzionaria. Fu arrestato e processato il 15 giugno per aver proferito minacce contro il nuovo re, ma venne poi prosciolto. Nel giro di un mese fu nuovamente arrestato e questa volta condannato a sei mesi di reclusione nella prigione di Sainte-Pelagie.

Nello stesso periodo l'Académie respinse un altro manoscritto di Galois e Poisson affermò riguardo al suo lavoro che gli argomenti non erano sufficientemente chiari né pienamente sviluppati perché fosse possibile giudicare della loro correttezza. Egli rispose rifiutando il giudizio dell'Académie e cercò di far pubblicare i suoi studi da un amico, il sansimoniano Auguste Chevalier. Un mese dopo aver lasciato la prigione morì in seguito a un oscuro duello. Nella notte precedente scrisse a Chevalier una lettera, nella quale riassumeva i risultati della sua teoria e la mattina successiva, il 30 maggio 1832 si recò sul luogo del duello fatale. Colpito all'addome, morì in ospedale il giorno successivo. Il suo funerale fu l'occasione per una dimostrazione repubblicana che provocò una settimana di disordini.

Sono state avanzate numerose ipotesi, per lo più politiche, riguardo alle ragioni di quel duello e sono stati versati fiumi di inchiostro per identificare l'antagonista. La risposta più verosimile è che si sia avverata una profezia che lo stesso Galois aveva formulato in prigione, come fu raccontato da Raspail: "morirò in un duello per colpa di una smorfiosa che non vale niente. Perché? Perché mi inviterà a vendicare il suo onore, che qualcun altro ha compromesso".

Dopo la morte di Galois e nonostante la stampa da parte di Chevalier di alcuni dei suoi studi, la comunità matematica francese rispose con il silenzio. Solamente con la pubblicazione dei suoi lavori nella rivista di Liouville, nel 1846, il vento cambiò direzione. Presumibilmente, Liouville venne a conoscenza di quei contributi perché Richard aveva appena scoperto un altro brillante studente, il giovane Charles Hermite. In seguito altri matematici (Betti in Italia, Dedekind e Kronecker in Germania) cominciarono a interessarsi alla teoria di Galois. Negli anni Sessanta il matematico francese Camille Jordan evidenziò il fatto che Galois aveva posto la teoria delle equazioni su fondamenta definitive mediante il concetto di 'gruppo di sostituzioni' e la distinzione cruciale tra gruppi semplici e gruppi composti. In quel periodo Jordan stava elaborando una teoria dei gruppi di permutazioni così generale da poter essere posta a fondamento dell'intera teoria dei gruppi finiti. La transizione dalle equazioni polinomiali alla teoria dei gruppi poteva ritenersi portata a termine.

Origini della teoria dei gruppi finiti di permutazioni

Nella sua approfondita analisi, Wüssing (1969) ha individuato diverse radici del concetto di gruppo. Una è la teoria dei gruppi di permutazioni, che ha ricevuto un impulso definitivo dal lavoro di Galois, specialmente quando cominciò a interessarsene Cauchy, che scrisse per la prima volta sui gruppi di permutazioni nel 1815. Il suo lavoro fu poi utilizzato da Abel nell'analisi delle equazioni di quinto grado e questa è una delle ragioni per le quali la trattazione di Abel venne ritenuta superiore a quella di Ruffini. Nel 1845 Cauchy fornì una illustrazione molto chiara dei gruppi di permutazione. Egli era a conoscenza del ritrovamento del lavoro di Galois ed esistono indizi che lasciano supporre che questo sia stato il motivo che lo indusse a riprendere in considerazione l'argomento.

Cauchy considera un allineamento di oggetti numerati e i suoi possibili rimescolamenti, che denomina permutazioni e pertanto ognuna di esse è un'azione, una trasformazione. Egli scrive, per esempio:

per indicare che l'oggetto numero 1 viene spostato nella posizione numero 2, l'oggetto numero 2 nella posizione numero 3 e infine l'oggetto numero 3 nella posizione numero 1. Per indicare una permutazione introduce anche la cosiddetta 'forma ciclica', che, nell'esempio precedente, è (1, 2, 3). La ripetizione di questa permutazione genera la permutazione (1, 3, 2) e una ulteriore ripetizione lascia fissi gli oggetti numerati con 1, 2 e 3. In questo caso Cauchy afferma che la permutazione ha ordine 3. Inoltre, egli osserva che una permutazione che può essere scritta come un ciclo di lunghezza n ha ordine n.

Egli prende in considerazione i prodotti di permutazioni (ottenuti applicando in successione due permutazioni) e osserva che il risultato dipende dall'ordine di applicazione: in generale, se A e B sono permutazioni, AB≠BA. Cauchy denota i prodotti della permutazione di A con sé stessa con A², A³, e così via e definisce inversa di A, indicandola con A⁻¹, la permutazione che annulla l'effetto della permutazione A. Egli nota che le permutazioni A e BAB⁻¹ sono simili l'una all'altra nel senso che, se si consente di rinumerare gli oggetti, esse sono la stessa permutazione. Procedendo in questo modo egli elabora una teoria elementare dei gruppi di permutazioni, considerando le collezioni di permutazioni generate da tutti i possibili prodotti delle permutazioni ottenute da un dato insieme. Cauchy chiama una tale collezione sistema delle permutazioni derivate dal dato insieme (secondo l'attuale terminologia: gruppo delle permutazioni generato dal dato insieme). Anche se le permutazioni così generate permutano n oggetti, il loro gruppo non è necessariamente così grande da coincidere con il gruppo di tutte le permutazioni di n oggetti. Cauchy dimostra però che il numero degli elementi del loro gruppo deve necessariamente dividere n!, cioè il numero degli elementi del gruppo di tutte le permutazioni di n oggetti.

Cauchy fa un'osservazione che, anche se non lo riconosce esplicitamente, si ricollega alle idee di Galois: egli nota che si possono avere due 'sistemi' (chiamiamoli A_i e B_j) tali che, A_iB^j=B^jA_i per ogni coppia i, j o, più in generale, tali che A_iB_j=B_j′A_i′, per opportuni i′, j′. Un sottogruppo normale secondo la terminologia di Galois è, secondo Cauchy, un sistema (di A_i) i cui elementi appartengono a un gruppo più grande (i B_j) e che soddisfano equazioni della forma B^jAⁱB^j−1=A_i′. Osservazioni di questo genere sollevano il problema di quanto Cauchy conoscesse del lavoro di Galois prima che lo stesso fosse regolarmente pubblicato e suggeriscono che, presumibilmente, egli sapeva soltanto che Galois aveva utilizzato le permutazioni per affrontare il problema della risolubilità delle equazioni algebriche per radicali.

La successiva serie importante di risultati è dovuta a Serret e Camille Jordan, che negli anni Sessanta del XIX sec. svilupparono una teoria dei gruppi di permutazioni in cui viene ancora utilizzato il linguaggio di gruppi di permutazioni, ma i cui concetti sono implicitamente più generali. Jordan in particolare amplia enormemente le finalità della teoria e come Serret, utilizza la teoria di Cauchy sui gruppi di permutazioni per chiarire il lavoro di Galois. Egli chiama 'ordine' di un gruppo di permutazioni il numero dei suoi elementi e dimostra che se un gruppo H è contenuto in un altro gruppo G (cosicché H è un sottogruppo di G) allora l'ordine di H divide l'ordine di G. Tale risultato, che generalizza alcune conclusioni alle quali era già pervenuto Lagrange, è noto appunto come teorema di Lagrange. Jordan conclude il suo Commentaire sur Galois (1869) osservando che sarebbe stato utile classificare tutti i gruppi in funzione del modo in cui sono decomponibili in una successione di sottogruppi, ognuno normale nel sottogruppo successivo. Questo era un passo importante per focalizzare le idee di Galois dal problema originale della risolubilità delle equazioni algebriche per radicali al problema, più generale, dell'analisi dei gruppi finiti.

Nel suo libro del 1870, il Traité des substitutions et des équations algébriques, Jordan sviluppa concetti che gli consentono di scomporre un gruppo G in gruppi più piccoli e in particolare di analizzare quando sia possibile scomporre G in una successione di sottogruppi consecutivi, con la proprietà che se H_i e H_j sono sottogruppi successivi e H_i è un sottogruppo normale di H^j allora l'ordine di H_j è un multiplo primo dell'ordine di H_i. Se G è il gruppo associato a un'equazione algebrica, questa è la condizione necessaria e sufficiente affinché l'equazione sia risolubile per radicali; qui il problema viene, però, completamente inglobato in quella che Wüssing chiama la teoria dei gruppi di permutazioni, che si può applicare a ogni gruppo, indipendentemente dal fatto che i suoi elementi siano ottenuti o pensati come permutazioni. Tipici tra i concetti introdotti da Jordan sono quelli di 'centralizzatore' di un elemento A in un gruppo G (definito come l'insieme degli elementi B che commutano con A, ovvero tali che AB=BA) e di 'normalizzatore' di un sottogruppo H (il più grande sottogruppo K di G tale che H è normale in K). Tali concetti hanno un dominio di applicazione più ampio della teoria dei gruppi di permutazioni e si applicano a ogni collezione di oggetti che sia chiusa rispetto a una legge di composizione. Lo stesso vale per il concetto di applicazione tra gruppi che preserva la composizione: se G e G′sono i gruppi e Φ è l'applicazione, si dice che Φ preserva la composizione se Φ(g₁g₂)=Φ(g₁)Φ(g₂). In questo contesto, Jordan chiarisce quando due gruppi vanno considerati sostanzialmente uguali e quando l'uno è l'immagine dell'altro. Illustra poi nel massimo dettaglio il ruolo che la teoria dei gruppi può svolgere in altri ambiti della matematica, ovunque si possano trovare simmetrie.

Sebbene molte copie del suo libro fossero state distrutte durante gli eventi della Comune di Parigi, esso esercitò comunque una grande influenza, favorendo lo studio della teoria dei gruppi come disciplina indipendente. Uno dei primi a dare importanti contributi fu il matematico norvegese Ludwig Sylow, il quale nel 1872 dimostrò una proposizione che inverte parzialmente il teorema di Lagrange: se un numero primo p divide l'ordine di un gruppo G, allora esiste un sottogruppo H di G l'ordine del quale è uguale alla più grande potenza di p che divide l'ordine di G. Tale affermazione non è vera se p non è primo: per esempio, si può dimostrare che esistono gruppi di permutazioni di ordine 12 che non ammettono sottogruppi di ordine 6. Nella dimostrazione originale di Sylow si ritrovano diversi importanti concetti, quali quello di normalizzatore e altri, più antichi, che si devono a Cauchy o addirittura a Lagrange.

In particolare, Sylow si basa su un classico risultato di Cauchy secondo il quale se un numero primo p divide l'ordine di un gruppo G, allora esiste un sottogruppo H di G di ordine p. Le dimostrazioni successive del teorema di Sylow, che sono state numerose, culminano in quella di Frobenius del 1887, in cui viene deliberatamente evitato qualsiasi accenno al linguaggio delle permutazioni, passando così alla concezione astratta della moderna teoria dei gruppi.

È interessante notare come le cose si siano sviluppate diversamente in Germania dove Kronecker, uno dei primi ad apprezzare il lavoro di Galois, non era particolarmente attratto dal linguaggio della teoria dei gruppi. Cionondimeno, sembra che Kronecker sia stato il primo a fornire la definizione astratta di gruppo commutativo finito (un gruppo per cui AB=BA per ogni coppia di suoi elementi A e B). Anche Richard Dedekind sviluppò l'idea di gruppo astratto nel contesto della teoria di Galois. Come ha provato Purkert (1976), egli tenne alcuni cicli di lezioni sulla teoria di Galois a Gottinga tra il 1856 e il 1858, pur non pubblicando nulla in merito fino al 1894, anno in cui comparve il famoso undicesimo supplemento alle lezioni di Peter Gustav Lejeune Dirichlet sulla teoria dei numeri. I manoscritti delle sue lezioni dimostrano però quanto egli si sia spinto oltre i concetti sui gruppi che nel frattempo aveva pubblicato. Dedekind spiega che il concetto di gruppo di permutazioni si generalizza in quello di gruppo finito astratto e introduce le definizioni di sottogruppo normale e di decomposizione in classi laterali. Egli dimostra che le classi laterali di un sottogruppo normale K formano esse stesse un gruppo, nel quale K è l'unità. Kronecker e Dedekind mantengono il legame con le equazioni algebriche più strettamente di Jordan; di conseguenza, nei lavori realizzati in Germania si presta maggiore attenzione ai 'campi' di numeri ottenuti aggiungendo ai numeri razionali le radici di un'equazione algebrica.

Nel suo libro Wüssing mostra altresì come alcune delle radici della teoria dei gruppi si possano far risalire alle idee sulla geometria che circolavano intorno alla metà del XIX secolo. In particolare, nel 1872, in occasione della sua nomina a professore ordinario all'Università di Erlangen ‒ quando aveva soltanto 23 anni ‒, Christian Felix Klein distribuì un opuscolo contenente una rassegna comparativa dei concetti fondamentali della geometria. Il Programma di Erlangen, come venne chiamato intorno agli anni Novanta del XIX sec., quando fu meglio conosciuto, si basava sull'affermazione dell'esistenza di diverse geometrie (proiettiva, affine, euclidea e anche non euclidea), ognuna caratterizzata da un gruppo di trasformazioni: le proprietà invarianti rispetto al gruppo sono le proprietà geometriche, vale a dire le proprietà di una specifica geometria. Come conseguenza delle relazioni che esistono tra questi diversi gruppi (per es., il gruppo euclideo è un sottogruppo del gruppo affine, che a sua volta è un sottogruppo del gruppo proiettivo) è possibile definire una gerarchia tra le corrispondenti geometrie.

Autori successivi si sono spinti oltre. Il legame tra gruppi e geometrie è, se possibile, ancora più stretto nel lavoro di Poincaré, sia sul versante tecnico sia su quello filosofico ed è spinto molto più in profondità dal lavoro dell'amico di Klein Sophus Lie, il quale classificò tutti i gruppi che agiscono su spazi di dimensioni 1, 2 e 3.

La teoria dei gruppi e la cristallografia

Lo studio della cristallografia costituisce un'altra fonte per la teoria dei gruppi. Infatti, come afferma Scholz (1989), i cristallografi, prima ancora di avere conferma da osservazioni sperimentali ottiche, hanno definito un cristallo più o meno come un oggetto simmetrico posto in un punto di un reticolo cristallino. Essi hanno poi sintetizzato le osservazioni sperimentali disponibili formulandole in termini di reticoli, dotati di certe simmetrie e tali che a ogni loro vertice può essere aggiunto un 'solido' avente altre simmetrie, ma non hanno attribuito necessariamente un significato fisico a queste costruzioni. Mentre dibattevano le ipotesi mediante le quali spiegare i concetti matematici sottostanti, i cristallografi hanno contribuito anche ad approfondire gli stessi concetti, impegnandosi a definire teoremi di classificazione delle strutture cristalline. Così facendo, essi hanno creato un ramo della geometria sufficientemente profondo e flessibile, cosicché è stato in seguito agevole riformulare le loro idee nel linguaggio della teoria dei gruppi. Questo, come osserva Scholz, è un aspetto caratteristico delle applicazioni di successo della matematica al mondo reale.

Per comprendere meglio la questione si consideri il caso bidimensionale. Un reticolo è un insieme di punti del piano della forma {m₁e₁+m₂e₂}, dove e₁ e e₂ sono vettori indipendenti e m₁ e m₂ sono interi. Può essere d'aiuto immaginare il parallelogramma di vertici 0, e₁, e₂, e₁+e₂ come una mattonella, copie della quale ricoprono interamente il piano. Ciò che è importante è l'insieme delle simmetrie di un reticolo. Può non esserci alcuna altra simmetria oltre quelle (dette 'traslazioni del reticolo') che traslano 'in blocco' la mattonella di un tratto pari a m₁e₁+m₂e₂; ma, se, per esempio, le mattonelle sono quadrate, ci sono molte rotazioni e riflessioni del reticolo che lo trasformano in sé stesso e se, inoltre, la mezza mattonella 0, e₁, e₂ ha la forma di un triangolo equilatero esistono ulteriori, differenti simmetrie. Di fatto, si può dimostrare che, secondo questo punto di vista, esistono 17 distinti reticoli piani corrispondenti a 17 distinti cristalli bidimensionali, ovvero, come spesso si dice, a 17 tipi possibili di modelli reticolari. La dimostrazione si basa principalmente sull'osservazione che il reticolo deve essere costituito da mattonelle e 'sottomattonelle' di forma triangolare o rettangolare; mentre la forma pentagonale non è possibile. Questa condizione viene detta talvolta 'restrizione cristallografica'.

È di un certo interesse individuare il periodo in cui tale teorema di classificazione cominciò a essere noto; in proposito, sembra che, pur di contare con grande attenzione i colori nei disegni, tutti i 17 tipi possibili di modelli si possano osservare nell'Alhambra, presso Granada in Spagna. Non è chiaro, però, se i disegnatori e i costruttori islamici fossero a conoscenza di una dimostrazione del fatto che tali modelli esauriscono tutte le possibilità o se almeno si fossero posti il problema.

Il cristallografo che più ha influenzato i matematici fu Auguste Bravais (1811-1863) che studiò all'École Polytechnique dove poi insegnò come professore di fisica, dal 1845. Nel 1849 egli scrisse un libro sulla cristallografia, al quale fece seguito nel 1850 un lungo articolo nella rivista di Liouville. Bravais distinse nettamente fra simmetrie del reticolo e simmetrie che si manifestano quando tutti i vertici vengano identificati con uno solo, scelto arbitrariamente. Nel linguaggio della teoria dei gruppi, questa seconda classe di simmetrie corrisponde al quoziente del gruppo completo delle simmetrie del reticolo, modulo il sottogruppo delle traslazioni. Bravais scoprì che queste simmetrie possono avere solo certi ordini: 2, 3, 4 o 6, ma non, per esempio, 5, la vera restrizione cristallografica. Basandosi su questa caratteristica, egli classificò i reticoli in 7 tipi (o 14, a seconda di come vengono contati).

Nel suo libro (1856), una riedizione di parecchi articoli già pubblicati precedentemente su diverse riviste, Bravais espose una teoria della struttura dei cristalli basata sulla classificazione dei reticoli. Egli trovò 71 dei 73 tipi delle possibili combinazioni, ma storicamente il libro è importante per essere stato giudicato positivamente da parte non soltanto dei cristallografi, ma ben presto anche dai matematici e, in particolare, da Camille Jordan.

Anche Jordan studiò alla École Polytechnique, ma fu nella seconda parte della sua carriera scolastica, all'École des Mines, che venne a conoscenza per la prima volta della cristallografia di Bravais. Nel 1869, ispirandosi al lavoro del suo predecessore, che ammirava, ma i cui risultati riteneva dovessero ancora essere sviluppati in piena generalità, egli si pose l'obiettivo di scoprire tutti i gruppi che possono agire sullo spazio euclideo tridimensionale, sia in modo continuo sia in modo discontinuo. Individuò così un totale complessivo di 174 tipi di gruppo, dei quali 50 sono quelli che egli chiamò continui, 5 sono finiti e 59 sono discontinui ma spostano 'in blocco' una regione finita (una mattonella tridimensionale). I rimanenti sono gruppi per diverse ragioni irrilevanti. Per esempio, 16 tra questi ultimi trasformano un piano in sé e quindi spostano colonne infinite. È più naturale pensarli come gruppi di simmetria del piano, e infatti essi coincidono con 16 dei 17 gruppi costituenti i modelli reticolari. Come ci si poteva aspettare, in questi lavori pionieristici ci sono altre omissioni, riguardanti 6 dei 65 gruppi dei moti propri della cristallografia, nonché alcune ripetizioni. Nondimeno, essi costituiscono un passo fondamentale verso il raggiungimento dell'obiettivo di individuare tutti i gruppi dello spazio tridimensionale.

Tali lavori, inoltre, rappresentano un progresso anche rispetto al lavoro di Bravais, rendendo preciso ed esplicito ciò che lo stesso Bravais aveva formulato in termini geometrici meno sistematici e fornendo ragioni profonde, basate sulla teoria dei gruppi, per ignorare molti dei suoi reticoli. Tuttavia tali risultati non furono presentati in maniera convincente e, per varie ragioni, fu necessario attendere più di vent'anni prima che i cristallografi li facessero propri. Alcuni matematici, quali Leonhard Sohncke e B. Minnigerode, si sono interessati all'argomento. Il fisico Pierre Curie ha rielaborato i risultati di Bravais, considerandoli incompleti. Il loro lavoro ha attratto altri studiosi, tra i quali il matematico Arthur Schoenflies (studente di Klein) e il mineralogista e cristallografo Evgraf Stepanovič Fedorov. Lavorando indipendentemente l'uno dall'altro durante gli anni Ottanta del XIX sec., Schoenflies individuò, prima del 1889, 227 gruppi spaziali cristallografici e Fëdorov 230. Schoenflies accettò quest'ultimo numero e scrisse un resoconto matematicamente soddisfacente della struttura dei cristalli, basato sullo stesso risultato. Un'indicazione dell'importanza che i matematici hanno attribuito a questo risultato è che esso interviene nella formulazione del diciottesimo problema di Hilbert, nel quale ci si domanda se sia vero che in uno spazio euclideo, di dimensione qualsiasi, esiste solo un numero finito di gruppi cristallografici. Il problema è stato risolto affermativamente, poco prima dell'inizio della prima guerra mondiale, da un altro studente di Klein: Ludwig Bieberbach.

Capitoli ulteriori della teoria dei gruppi. La teoria delle rappresentazioni

La teoria dei gruppi finiti ha attraversato due fasi importanti: la definizione del concetto di gruppo astratto (Dedekind, Cayley e, per i gruppi abeliani, Kronecker) e la prima elaborazione della teoria delle rappresentazioni.

Teoria delle rappresentazioni

Quando l'interesse della ricerca si è spostato dai gruppi delle permutazioni e dai gruppi delle trasformazioni geometriche alla nozione di gruppo astratto, i principali artefici della teoria dei gruppi hanno cominciato ad apprezzare i vantaggi di una rappresentazione dei gruppi in termini di strutture i cui elementi fossero 'oggetti concreti'. Ciò di cui si avvertiva la necessità era la possibilità di rappresentare un gruppo come gruppo di trasformazioni lineari, così da poter identificare ogni suo elemento con una matrice; peraltro, l'enfasi si spostava ora sull'insieme di tutte le possibili rappresentazioni, piuttosto che su quelle che avevano fatto la loro comparsa occasionale durante lo studio di un problema. Significativamente, i problemi principali della teoria dei gruppi stavano per sollecitare lo sviluppo delle tecniche della teoria delle rappresentazioni, mentre continuavano a resistere ai metodi astratti.

I pionieri della teoria delle rappresentazioni dei gruppi furono Frobenius e Isai Schur in Germania e Burnside in Inghilterra. Una fonte importante per la conoscenza del lavoro iniziale di Frobenius è la sua corrispondenza con Dedekind. Questa è stata riscoperta soltanto nel 1972, è stata analizzata da Hawkins (1974) e viene ora pubblicata a cura di Haubrich. Le lettere furono scritte in tre periodi: 1882-1883, 1895-1898 e 1901. Quelle scritte nel maggio 1896 sono particolarmente importanti, poiché mettono in evidenza lo sviluppo del pensiero di Frobenius durante l'elaborazione della teoria dei caratteri e mostrano, tra l'altro, come l'ordine della pubblicazione dei suoi lavori risulti invertito rispetto all'ordine in cui ne furono scoperti i risultati. Frobenius difatti evitava di far circolare informazioni fino a quando non era in grado di dimostrare le conclusioni più importanti alle quali era pervenuto.

L'interesse di Frobenius per la teoria dei gruppi si è sviluppato a partire da diversi filoni di ricerca matematica. Da studente, a Berlino, si era familiarizzato con la teoria di Weierstrass delle forme bilineari e aveva continuato a scrivere su questo argomento e su quello, ancora più complesso, delle 'funzioni theta', funzioni di più variabili legate tra loro da quello che egli chiamò, in modo appropriato, un labirinto di formule. In entrambi gli argomenti, la considerazione delle simmetrie e l'utilizzazione dei concetti propri della teoria dei gruppi gli furono di aiuto nel superare le difficoltà incontrate. L'uso da parte di Frobenius di matrici e determinanti, caratteristico del tempo, non viene analizzato in questa sede, ed è sufficiente ricordare che la possibilità di ridurre al minimo il ricorso a queste tecniche si deve al lavoro di autori successivi.

In effetti, l'idea di 'carattere di un gruppo' precede Frobenius di almeno una generazione e spiega le ragioni della sua corrispondenza con Dedekind. L'origine risale infatti ai lavori di Gauss in teoria dei numeri. Quei lavori hanno avuto un'importanza straordinaria ‒ trasformando definitivamente la teoria dei numeri in un ramo centrale della matematica ‒ ma erano anche molto difficili da comprendere, e furono oggetto di approfonditi studi da parte di alcuni tra i migliori matematici della generazione successiva. Dirichlet tenne corsi su quella teoria e le sue lezioni furono pubblicate da Dedekind. Il libro ebbe grande successo e molte edizioni, anche perché Dedekind se ne servì per pubblicare come appendici molti dei suoi studi più importanti sull'argomento.

Queste appendici trattano tra l'altro il concetto di carattere di un gruppo nel caso dei gruppi abeliani. Un carattere di un gruppo G è una funzione definita su G che preserva il prodotto e assume valori nel gruppo moltiplicativo dei numeri complessi non nulli. Dirichlet aveva utilizzato tale funzione, pur senza pensarla come carattere di un gruppo, del quale a quel tempo non esisteva ancora una definizione generale, per dimostrare l'esistenza di infiniti numeri primi in ogni progressione aritmetica. Kronecker aveva ripreso il lavoro di Gauss mostrando, in modo molto semplice, che in esso, tra l'altro, è contenuta la dimostrazione del fatto che i gruppi abeliani sono costituiti da gruppi ciclici. Frobenius, in uno studio congiunto con Stickelberger (1879), applicò questo risultato al gruppo dei resti modulo un numero non primo. Nella terza edizione delle lezioni di Dirichlet sulla teoria dei numeri, Dedekind spiega in maniera dettagliata, per la prima volta, il concetto astratto di carattere di un gruppo abeliano finito G, definendolo come una funzione α da G al gruppo delle radici complesse dell'unità, con la proprietà che Φ(g1g2)= =Φ(g1)Φ(g2).

Questo procedere verso l'astrazione era condiviso da Heinrich Weber, che aveva seguito le lezioni di algebra superiore di Dedekind quando era studente a Gottinga, e aveva poi collaborato con lui alla cura della prima edizione dei Werke di Riemann. Nel 1882 Weber adattò la dimostrazione di Dirichlet dell'esistenza di infiniti numeri primi in una progressione aritmetica, per dimostrare che una forma quadratica assume infiniti valori primi. In questo lavoro egli pose grande enfasi sulla teoria dei caratteri dei gruppi abeliani (analogamente a quanto farà nel secondo volume del Lehrbuch der Algebra (Trattato di algebra) che, pubblicato nel 1896, riscosse grande successo.

Il contributo più importante di Frobenius fu l'elaborazione della teoria dei caratteri dei gruppi non abeliani, un'estensione che in precedenza non era stata considerata. La definizione di Weber era sufficiente a definire i caratteri in questo contesto più generale, ma l'esistenza di caratteri 'non banali' è tutt'altro che ovvia e, prima di Frobenius, non si avevano motivazioni per procedere a tale estensione. Secondo Frobenius la maggior parte della matematica, e in particolare buona parte della teoria dei numeri, è essenzialmente teoria dei gruppi e molti gruppi, se non quasi tutti, sono non abeliani. Negli anni Ottanta egli si stava interessando, tra l'altro, a problemi relativi alla teoria algebrica dei numeri, argomento di cui Dedekind era un esperto riconosciuto, e pertanto fu naturale mettersi in contatto con lui. Le lettere che gli scrisse espongono chiaramente le difficoltà del suo percorso teorico e il tentativo di superarle attraverso lo studio delle funzioni Φ definite su un gruppo (o su sistemi più complicati), aventi la proprietà che Φ(g1g2)=Φ(g1)Φ(g2).In particolare tali funzioni hanno anche la proprietà che Φ(g1hg1−1)=Φ(h), ovvero assumono lo stesso valore su elementi che appartengono alla stessa classe di coniugio (in un gruppo, gli elementi h e g1hg1−1 si dicono coniugati).

Il riconoscimento dell'importanza delle classi di coniugio in un gruppo finito spinse Frobenius a riflettere sulla relazione tra il numero k delle classi di coniugio e un altro numero: il numero l dei fattori distinti del determinante del gruppo, che Frobenius definì in questo modo: siano g1=e, g2,…,g_n gli elementi di un gruppo G e si supponga di utilizzarli come indici per n variabili xg1,…,xg_n. Si formi il polinomio in queste variabili, che è dato dal determinante della matrice che ha sulla i-esima riga e j-esima colonna l'elemento x_gi_gj−1. Ci porterebbe troppo lontano spiegare perché Frobenius era interessato a un oggetto così complesso e d'altra parte le generazioni successive si sono impegnate a fondo per poterne fare a meno. È chiaro che Frobenius adottava la pratica consueta in quegli anni di studiare un gruppo (o qualsiasi altra situazione che presentasse una simmetria) costruendo polinomi opportuni. Frobenius congetturò che i due numeri k e l fossero uguali e nel giro di pochi giorni pervenne a una dimostrazione che inviò a Dedekind. Passaggio fondamentale della dimostrazione era la sostituzione delle variabili originarie con variabili di un nuovo sottoinsieme più piccolo, in corrispondenza biunivoca con le classi di coniugio del gruppo. Nelle nuove variabili, ogni fattore irriducibile del determinante del gruppo appariva come un singolo fattore lineare, ripetuto un certo numero di volte (analogamente al modo in cui un fattore primo appare con una data potenza nella fattorizzazione di un numero intero). Ciò indusse Frobenius a concludere che l'analisi del determinante di un gruppo porti in modo naturale a studiare le funzioni definite sulle classi di coniugio. Egli ipotizzò allora che altri due numeri, e e f, fossero uguali. "Sarebbe meraviglioso se e=f", scrisse a Dedekind il 26 aprile 1896 essendo convinto della correttezza di tale ipotesi e aggiunse: "Le convinzioni soggettive sono in effetti migliori delle dimostrazioni, ma al mondo crudele non bastano" (in Hawkins 1974, p. 235). Per tutta l'estate Frobenius non fu capace di dimostrare quella uguaglianza, finché i suoi sforzi furono finalmente coronati da successo il 6 settembre 1896, utilizzando metodi completamente diversi da quelli che aveva adottato fino a quel momento.

Il fatto di non essere riuscito per cinque mesi a trovare una dimostrazione spiega perché gli articoli che egli pubblicò in quel periodo hanno il contenuto che conosciamo. I due numeri e, f furono tenuti nascosti, perché Frobenius aveva l'impressione di aver stabilito un risultato centrale della nuova teoria, ma non era in grado di dimostrarlo. Egli non voleva che il risultato fondamentale di una teoria di sua elaborazione venisse dimostrato da qualcun altro.

Una volta pervenuto alla dimostrazione, per Frobenius fu possibile pubblicare la teoria dei caratteri di un gruppo così come l'aveva concepita (gli articoli apparvero nel 1897). Tale teoria chiarisce come la rappresentazione naturale di un gruppo su sé stesso si decomponga in rappresentazioni che, secondo la terminologia moderna, sono dette 'sottorappresentazioni irriducibili'. Per comprendere questo aspetto, si utilizzino gli elementi {g1=e,g2,…,g_n} di G come indici per n elementi e_g1,…,e_gn costituenti una base di uno spazio vettoriale n-dimensionale V_n. L'applicazione del gruppo in sé, che moltiplica a destra ogni suo elemento g_i per un elemento fissato g_j−1, trasforma g_i in g_ig_j−1. Tale rappresentazione induce un'applicazione lineare di V_n in sé, che manda e_gi in e_gi_gj−1; a essa è pertanto associata una matrice. Ogni elemento del gruppo quindi può essere rappresentato in modo naturale con una matrice che è detta 'rappresentazione regolare destra'. È ovvio che la matrice è diversa se gli elementi della base vengono presentati in ordine diverso, ma intorno al 1890 erano già state sviluppate alcune teorie che, al di là di tali differenze superficiali, permettono di comprendere le caratteristiche principali delle applicazioni lineari. Si tratta della teoria dei divisori elementari di Weierstrass, molto familiare a Frobenius, e della teoria delle forme canoniche di Jordan. Era ben noto che, cambiando la base di uno spazio vettoriale V, la matrice A di una trasformazione lineare di V in V si trasforma nella matrice B−1AB; pertanto, secondo tale approccio, le caratteristiche fondamentali di una matrice A sono quelle che ha in comune con tutte le matrici della forma B−1AB, in breve, con tutte le matrici coniugate. Tra queste ci sono il determinante di A e la sua traccia, che è definita come la somma dei suoi elementi diagonali. Secondo la terminologia moderna, ciò che Frobenius aveva scoperto era la teoria dei caratteri di un gruppo, ossia delle tracce delle sue rappresentazioni.

La rappresentazione regolare di un gruppo di ordine n permette di considerare i suoi elementi come trasformazioni lineari che agiscono su uno spazio vettoriale di dimensione n, ma può accadere che il gruppo agisca come gruppo di trasformazioni lineari su uno spazio di dimensione più piccola e che la rappresentazione regolare possa venire decomposta. Questo è il punto nel quale compare l'ipotesi di Frobenius, secondo la quale e=f. È lecito domandarsi quale sia la dimensione di uno spazio vettoriale nel quale sia definita una rappresentazione di G come gruppo di trasformazioni lineari; tale dimensione si chiama grado della rappresentazione e si indica con il numero e. È possibile chiedersi, inoltre, quante volte questa rappresentazione si presenti nella rappresentazione regolare: tale numero si indica con f. Per comprendere questo concetto si osservi che, se un gruppo ammette una rappresentazione come gruppo di trasformazioni lineari di uno spazio vettoriale V e un'altra rappresentazione su uno spazio vettoriale W, allora esiste (ovviamente) una terza rappresentazione, detta somma, nella quale il gruppo agisce contemporaneamente su V e W lasciando però distinti i due spazi. Viceversa, una rappresentazione si può presentare come somma e i sottospazi invarianti che contiene possono avere la stessa dimensione oppure no. La teoria relativa a tale decomposizione è governata dal lemma di Schur, un contributo del 1904.

Il teorema secondo il quale e=f afferma in sostanza che le 'sottorappresentazioni' irriducibili di una rappresentazione regolare appaiono in numero uguale al loro grado. Siano e_i i gradi delle rappresentazioni irriducibili; allora l'ordine n del gruppo è somma dei loro quadrati:

La [4] riassume una quantità straordinaria di informazioni. Si consideri per esempio il gruppo non abeliano S3, delle permutazioni su tre oggetti che ha ordine 6. È possibile scrivere 6 come somma di quadrati in due modi: 6=12+12+22, che è interessante, e 6=1+1+1+1+1+1, che è priva di interesse. La prima decomposizione ci dice che esistono due rappresentazioni a una dimensione e una a due dimensioni. Le rappresentazioni a una dimensione sono quella banale (gv=v per ogni g in G) e la rappresentazione gv=Segno(g)v, in cui G agisce sullo spazio vettoriale (a una dimensione) generato dal vettore v; il segno di una permutazione g vale +1 se l'elemento g agisce come una rotazione di V, −1 se agisce come una riflessione. La rappresentazione bidimensionale corrisponde all'azione usuale di S3 su un triangolo del piano. La rappresentazione associata alla decomposizione 6=1+1+1+1+1+1 di fatto non si presenta, perché il numero delle rappresentazioni irriducibili è uguale al numero delle classi di coniugio del gruppo, che in questo caso è 3 (l'identità, le tre permutazioni di ordine 2 e le due permutazioni di ordine 3). Così, non soltanto il grado della rappresentazione regolare deve uguagliare una somma di quadrati, ma anche il numero dei quadrati deve uguagliare il numero delle classi di coniugio del gruppo.

La tessera mancante di questo rompicapo è l'ulteriore, importante risultato, pubblicato da Frobenius e Schur nel 1904, che può essere così enunciato: due rappresentazioni sono distinte se, e solo se, hanno caratteri distinti (in breve: i caratteri caratterizzano).

Frobenius tuttavia non è il solo ad aver elaborato tale teoria. Va ricordato anche il matematico inglese William Burnside, uno di quei matematici di indubbio talento che però hanno bisogno di un argomento particolare per stimolare e far fiorire la loro genialità. Nessuno dubitava delle sue capacità ed egli lasciò Cambridge, dove era appassionato vogatore, per accettare un prestigioso incarico di insegnamento presso il Royal Naval College di Dulwich, sul Tamigi vicino Londra. Eletto membro della Royal Society nel 1893, svolse attività di ricerca di limitata rilevanza finché, per ragioni che restano tuttora oscure, non iniziò a occuparsi della teoria dei gruppi. Da quel momento, nei primi anni Novanta del XIX sec., e fino alla Prima guerra mondiale, la quantità e l'importanza delle sue pubblicazioni sono cresciute in maniera notevole.

Gli interessi di Burnside erano focalizzati sulla teoria dei gruppi in modo più preciso di quanto non lo fossero quelli di Frobenius. Egli aveva familiarità con i lavori tedeschi e con quelli di Lie, e il problema che si era posto consisteva nel determinare le classi di coniugio dei gruppi. Le idee di Lie lo allontanarono dai gruppi finiti, ma alcune informazioni su ciò di cui Frobenius si stava occupando lo fecero tornare sui suoi passi e lo spinsero a elaborare la teoria della decomposizione delle rappresentazioni appena descritta. Egli ribadì sempre l'indipendenza dei suoi risultati da quelli di Frobenius per quanto riguarda la teoria dei caratteri e ciò è giustificato dalle differenze tanto di metodo quanto di approccio che esistono tra i due. Tuttavia, Frobenius raggiunse per primo tali risultati e Burnside aveva letto la maggior parte dei suoi più importanti lavori prima di pubblicare i propri.

D'altro canto, Burnside ha sfruttato più di Frobenius la potenza della teoria delle rappresentazioni. Nel 1897 pubblicò la prima edizione del suo libro Theory of groups, nella quale non fa alcuna menzione della teoria delle rappresentazioni, ma dopo il 1898, ormai in grado di apprezzare il lavoro di Frobenius, la utilizzò per dimostrare risultati del tipo: ogni gruppo di ordine p^aq^b è risolubile. Il fatto che tale affermazione non possa essere dimostrata mediante metodi più elementari è una testimonianza eloquente della potenza dei nuovi metodi.

Sophus Lie

Uno dei rami principali della matematica del XX sec., ricco di intime connessioni con la fisica, è costituito senza dubbio dalla teoria dei gruppi di Lie e dalla teoria delle algebre di Lie, chiamate così in onore del matematico Sophus Lie (1842-1899). Lie fu molto amico di Christian Felix Klein, il cui Programma di Erlangen del 1872 è uno dei lavori ai quali si deve l'introduzione della teoria dei gruppi in geometria. Siccome Lie stesso continuò a scrivere a lungo su quelli che chiamava gruppi di trasformazioni, sembrerebbe ovvio che egli debba figurare con il suo lavoro in ogni storia della teoria dei gruppi nel XIX secolo. Il fatto che ciò non accada non dipende soltanto dagli storici ‒ con la notevole eccezione di Thomas W. Hawkins, che ha dedicato più di vent'anni proprio a ricerche su questo argomento. È anche vero che le idee di Lie non trovano posto agevolmente in una rassegna di quel periodo storico in quanto buona parte del lavoro di eminenti matematici del XX sec., quali Élie Cartan e Hermann Weyl, si può considerare come un tentativo differito di trasformare il lavoro di Lie nella importante teoria, ben integrata con il resto della matematica moderna, che oggi porta il suo nome.

Lie cominciò con la teoria delle equazioni differenziali, che rimase sempre un punto di riferimento nel suo lavoro. La sua prima ambizione, chiamata da Hawkins (1991) la sua idée fixe, fu l'elaborazione di una teoria di Galois delle equazioni differenziali. Ciò che intendeva con questa espressione e il modo in cui questa idée fixe lo condusse ai suoi risultati, dimostrano quanto profondamente egli fosse uomo del suo tempo. Il suo interesse iniziale riguarda i sistemi di equazioni lineari alle derivate parziali, analoghi a quelli studiati da Jacobi nella dinamica. Non è facile determinare un insieme completo di soluzioni per tali sistemi e la complessità del formalismo potrebbe mettere in difficoltà chiunque. Lie scoprì che è possibile sfruttare certe simmetrie del problema; ciò lo indusse a considerare operatori differenziali del primo ordine della forma

in n variabili x1,…,x_n. Seguendo una precedente idea di Poisson, egli definì prodotto degli operatori P_i e P_j l'operatore [P_i,P_j]==P_iP_j−P_jP_i, che è ancora del primo ordine, perché i termini della forma

si elidono. Lie si pose il problema di determinare le condizioni per l'esistenza di una base finita {P1,…,P_n} di operatori, tale che ogni operatore e ogni prodotto di coppie di operatori possano esprimersi come somma degli elementi della base. Se [P_i,P_i′]=P, allora la condizione che Lie cercava di imporre all'operatore prodotto si può determinare in funzione delle a_ij a_i′_j e delle loro derivate. Non ci interessa seguire Lie in questi complessi ragionamenti, ma è sufficiente osservare come egli insistesse sulla legge di composizione, richiedendole soltanto che fosse chiusa. Tutto ciò era in accordo con l'orientamento di Klein verso i gruppi di trasformazioni geometriche, ma dimostra anche quanto Lie fosse lontano da qualcosa che assomigliasse alla moderna definizione di gruppo.

Un altro argomento al quale Lie era interessato era la teoria ormai ben sviluppata delle equazioni differenziali ordinarie del primo ordine, per la quale si conoscevano non poche tecniche mediante le quali di solito si riconducevano a una semplice integrazione. Lie intendeva dare a questo insieme di artifici apparentemente ad hoc una spiegazione più sistematica, sempre in termini di simmetrie di operatori (Lie 1891; Ince 1926). Determinato ad affrontare tali problemi, egli focalizzò la sua attenzione sul tentativo di classificare i gruppi che implicavano un numero piccolo di variabili.

Il passo essenziale nel suo lavoro è il passaggio dalle trasformazioni infinitesime alle trasformazioni finite che esse generano. Si considerino, per esempio, le rotazioni del piano attorno all'origine. Ogni rotazione può essere rappresentata da una matrice; la matrice

descrive una rotazione di un angolo ϑ in senso antiorario. Muovendo di uno spostamento finito ogni punto del piano eccetto l'origine, essa costituisce un esempio di quella che più sopra si è chiamata trasformazione finita. Al variare di ϑ, ogni punto (diverso dall'origine) descrive un cerchio con centro nell'origine: il punto (x0,y0) viene spostato nel punto

Pertanto, ha senso chiedersi quale sia la direzione istantanea del moto del punto (x0,y0) e considerare la corrispondente trasformazione infinitesima. Poiché le tangenti al cerchio sono perpendicolari al raggio, la direzione istantanea del moto del punto (x0,y0) deve essere (−y0,x0). Per dimostrarlo, si possono utilizzare i metodi standard per la determinazione delle tangenti alle curve dipendenti da un parametro: differenziando rispetto al parametro e poi determinandolo di conseguenza. In questo caso il valore del parametro è zero, perché il punto (x0,y0) coincide con il punto [8] precisamente quando ϑ=0. Allora la tangente si ottiene valutando

per ϑ=0, ovvero

come richiesto. Lie generalizzò questo risultato familiare in due direzioni. Considera un numero n qualsiasi di variabili e le trasformazioni dipendenti da k parametri. Indicate con x le variabili x1,…,x_n e con a i parametri a1,…,a_k, le trasformazioni finite possono rappresentarsi nella forma x′=f(x,a). Le trasformazioni infinitesime associate a queste si ottengono differenziando le funzioni f rispetto ai parametri. Tipicamente, Lie scrisse le trasformazioni sotto forma di serie di potenze di a_i+δa_i ed esaminò i coefficienti delle δa_i (i quali corrispondono alle derivate prime in una serie di Taylor). In questo modo egli pervenne a equazioni della forma

oppure, ponendo x_i′−x_i=dx_i,

Posto

si riconosce in quest'ultima relazione la presenza dell'operatore differenziale

Tale operatore, applicato a una funzione f(x1,…,x_n) delle coordinate x1,…,x_n,, produce l'incremento infinitesimo di f corrispondente all'incremento infinitesimo di x:

[15]  f(x1+dx1,…,x_n+dx_n)=f(x₁,…,x_n)+X_kf(x₁,…,x_n)dt_k.

Lie si chiese allora quando queste trasformazioni infinitesime formino un gruppo. Ciò accade se e solo se

Nel 1873 Lie cominciò a studiare il significato di quest'ultima equazione per valori piccoli di n. Indicato con k il numero dei parametri, egli riuscì a mostrare facilmente che ci sono soluzioni uniche per n=1 se k=2 o k=3, ma nessuna soluzione se k≥4. Se n=2 il problema si presentava più difficile e Lie ne pubblicò la soluzione nel 1876 in una rivista norvegese di cui era uno dei curatori e poi nuovamente nei "Mathematische Annalen" nel 1880. Nel frattempo risolse il problema anche per n=3, ma la soluzione era così complessa che preferì non renderla nota. Anche la soluzione per n=2 si basava sulla sua precedente analisi delle equazioni differenziali e delle famiglie di curve lasciate invariate da certi gruppi.

Di fronte a problemi di difficile soluzione i matematici cercano naturalmente di semplificare. In analogia con la teoria di Galois, i concetti naturali che bisognava introdurre erano quelli di invariante, di sottogruppo normale e di gruppo semplice. Poiché i gruppi che Lie stava studiando contengono elementi che si possono sia sommare sia moltiplicare tra loro (e pertanto costituiscono quella che oggi si chiama un'algebra) il termine 'normale' va sostituito con il termine 'ideale'. Un insieme di elementi forma un ideale J se è chiuso rispetto all'addizione e se [A,X] è in J per tutti gli A nell'algebra e tutti gli X nell'ideale. Si può dimostrare che l'insieme dei prodotti [X_i,X_i′] genera un ideale.

Lie trovò anche numerosi esempi espliciti, quali: il gruppo delle trasformazioni dello spazio proiettivo n-dimensionale, i gruppi di matrici e i gruppi che preservano alcune semplici forme differenziali. In particolare trovò esempi per ognuna delle famiglie infinite, delle quali più tardi Cartan dimostrerà l'esistenza in un lavoro sulla classificazione delle 'algebre di Lie'. Egli era particolarmente interessato ai gruppi che possono agire su una varietà di dimensione piccola, con il che egli intendeva uno spazio (euclideo, affine o proiettivo) in un numero qualsiasi di variabili. Riuscì a classificarli per n=1, 2 e 3 variabili deducendone i corrispondenti gruppi di trasformazioni. In effetti, il passaggio dagli operatori alle matrici si è rivelato cruciale, aprendo la strada allo studio delle algebre di Lie come esempi di algebre di matrici.

Intorno ai primi anni Ottanta del XIX sec. Lie divenne pessimista sulle prospettive della sua ricerca. Il lavoro era oneroso e anche quando lo aveva pubblicato in una rivista tedesca di eccellenza, i "Mathematische Annalen", non aveva suscitato molto interesse. Completata la sua formazione in Germania e in Francia, aveva fatto ritorno alla nativa Norvegia verso il 1870, dove aveva ottenuto l'incarico di docente a Oslo. Manteneva contatti epistolari con Mayer (di cui fu collega per un breve periodo, quando ricoprì l'incarico che fu di Klein a Lipsia), Klein e pochi altri. Non si era mai trovato bene in Germania e non parlava fluentemente il tedesco, ma in Norvegia si sentiva completamente isolato. Iniziò a prendere in considerazione l'idea di riscrivere le sue teorie partendo da zero, per dimostrare come avrebbero potuto trasformare la teoria delle equazioni differenziali. Per aiutarlo, Klein e Mayer fecero in modo di affiancargli Friedrich Engel, affinché quest'ultimo, mentre lavorava alla stesura della propria Habilitationsschrift, aiutasse Lie a riscrivere le proprie teorie.

L'idea ebbe successo. Engel conseguì l'abilitazione come Privatdozent nel 1885 e Lie pubblicò un lungo articolo nei "Mathematische Annalen". In quel periodo un altro giovane matematico, cresciuto alla scuola di Berlino, cominciava a informarsi sulle teorie di Lie. Aveva scoperto, con un certo ritardo, che il lavoro di Lie si sovrapponeva al suo. Questi era Wilhelm Karl Killing, insegnante del liceo di Braunsberg (Prussia orientale), privo di contatti scientifici, autore di un Programschrift nel quale si proponeva di classificare tutte le 'algebre di Lie' mediante la teoria delle radici caratteristiche di Weierstrass. Siccome una lettera di Killing a Lie non ebbe risposta egli si rivolse a Engel, avviando in tal modo una lunga corrispondenza che lo avrebbe aiutato a mantenere viva la sua creatività. Killing capì che la sovrapposizione con il lavoro di Lie era notevole, ma si sentiva incoraggiato nell'apprendere che il compito che si era posto, di determinare tutte le 'algebre di Lie semplici', era ritenuto meritevole di interesse da parte di Engel. D'altra parte Engel si rendeva conto che Killing, nonostante gli scrivesse da un luogo piuttosto remoto, padroneggiava bene una teoria così oscura, che egli stesso era stato inviato in Norvegia a imparare dal maestro.

Nell'estate del 1886, quando Klein lasciò l'incarico per trasferirsi a Gottinga, si liberò a Lipsia uno dei rari posti di professore ordinario e la cattedra fu assegnata a Lie. Engel lo seguì e Killing fece in modo di incontrarli per un paio di giorni. Lie restò colpito da alcune delle idee di Killing, ma notò che altre erano troppo imprecise. Si riavviò in tal modo un lento scambio di lettere, in cui Engel incoraggiava Killing a mettere per iscritto i risultati cui era pervenuto. Assicurava Killing che Klein avrebbe fatto in modo che il suo lavoro fosse pubblicato nei "Mathematische Annalen", e che questo lo avrebbe introdotto nella cerchia di Klein a Gottinga. Fino a quel momento Killing aveva pubblicato solamente nel "Journal für die reine und angewandte Mathematik", la rivista di Berlino. A partire dal 1888, Killing inviò a Klein un lavoro in quattro parti nel quale venivano classificate le algebre di Lie complesse semplici (di dimensione finita). Il lavoro si presentava incompleto, molti calcoli laboriosi vi erano omessi e alcuni casi non vi erano presi in considerazione. Per completarlo, si sarebbero dovuti trattare tutti i diversi casi in cui si presentavano radici reiterate, ma gli impegni scolastici non lasciavano molto tempo all'insegnante. Killing scelse di pubblicare comunque i suoi risultati senza nasconderne le imperfezioni.

Klein non era l'unico a ritenere che il solitario genio norvegese sapesse molto di più di quanto aveva scritto. Con Lie era in contatto Jean-Gaston Darboux, conosciuto a Parigi negli anni 1870-1871; quando Lie tornò nella capitale francese nei primi anni Ottanta Poincaré e Picard compresero rapidamente le sue concezioni. Nel 1888 Darboux organizzò a Lipsia la visita a Lie di due giovani matematici francesi: De Tannenberg e Vessiot. Prima di allora Picard, ispirandosi alle teorie di Lie, aveva elaborato una teoria di Galois delle equazioni differenziali lineari ordinarie; il suo lavoro fu sviluppato da Vessiot dopo il suo ritorno dalla Germania (Gray 1985). Darboux e altri, all'École Normale, trassero profitto dai contatti con Lie e alcuni giovani matematici francesi ne approfittarono negli anni a seguire. Uno di questi, Arthur Tresse, fece conoscere al suo amico Cartan il lavoro di Killing. Cartan decise di proseguire tale lavoro e riuscì a portarlo a conclusione. Nella tesi di Cartan è contenuta la prima classificazione esauriente delle 'algebre di Lie complesse semisemplici'. Essa giustifica le intuizioni di Killing, chiarisce le sue argomentazioni, corregge i suoi errori e le sue omissioni. Occorreva soltanto che il resto del mondo matematico si allineasse, ma questo avrebbe richiesto ancora molti anni.

La teoria dell'eliminazione e la soluzione delle equazioni algebriche in più variabili

Nel XVIII sec. il metodo preferito per formulare e risolvere molti problemi di matematica pura e applicata era quello di tradurlo in termini algebrici. Ciò conduceva spesso alla risoluzione simultanea di molte equazioni polinomiali in più variabili. Il metodo più ovvio era basato sulla speranza di eliminare le variabili una alla volta. Questo metodo si era però rivelato di difficile, talvolta impossibile, applicazione, come dimostra il semplice esempio della eliminazione della variabile y dalle equazioni x3+y3=3xy e x2+y2=1. Per trattare questo genere di problemi era stato sviluppato un nuovo ramo dell'algebra, la 'teoria dell'eliminazione'. Una significativa indicazione della sua importanza è costituita da questo passo dell'Académie des Marines (l'istituzione scientifica aggregata nel 1770 alla Marina francese): "L'eliminazione delle variabili è un metodo importante [della matematica], che deve essere perfezionato, sia perché l'estrema lunghezza dei calcoli ordinari lo rende così ripugnante sia perché la risoluzione generale delle equazioni dipende da esso" (in Rider 1982, p. 168).

Durante il XVIII sec. era stato compiuto uno sforzo considerevole per dimostrare che due curve, l'una di grado m e l'altra di grado n, hanno nm punti di intersezione. Tale risultato, che si deve a Étienne Bézout ‒ uno di coloro che si sono occupati del problema ‒ richiede significativi cambiamenti di punto di vista per poter essere accettato (prima ancora che dimostrato). Richiede anzitutto che sia accettato che due rette parallele 'si incontrino all'infinito', che due curve con un numero insufficiente di punti reali in comune si intersechino in punti complessi e, infine, che per due curve aventi un punto di tangenza quest'ultimo conti con molteplicità maggiore di uno nel computo delle loro intersezioni. Quest'ultimo aspetto era anche il più difficile da comprendere: perfino Euler aveva perso la speranza di trattarlo in modo soddisfacente. Anche quando il teorema di Bézout venne dimostrato, rimaneva il problema di determinare esplicitamente le radici, e questo trascendeva le possibilità dell'algebra. Per esempio, due curve definite, rispettivamente, da un'equazione quadratica e da un'equazione cubica si intersecano in sei punti, le cui ascisse sono le radici di un'equazione algebrica di grado 6, ma può non esistere alcuna formula algebrica per calcolarle.

La teoria dell'eliminazione ha ricevuto un impulso decisivo nel 1840 a opera del matematico James J. Sylvester, noto anche per essere stato il primo ebreo ad affermarsi nell'ambito della comunità matematica inglese. Egli osserva che se due curve, definite dalle equazioni algebriche f(x,y)=0 e g(x,y)=0 hanno punti in comune, allora questi sono comuni anche alle curve x^kf(x,y)=0 e x^lg(x,y)=0, qualunque siano k e l. Se f è di grado m in y e g di grado n e se si suppone, senza perdere di generalità, che m≥n, allora al variare di k tra 0 e n−1 e di l tra 0 e m−1 si ottiene un sistema di m+n equazioni per i punti di intersezione. Queste equazioni sono lineari nelle potenze di y e i loro coefficienti sono monomi in x. I coefficienti, tuttavia, sono solo m+n e pertanto esistono soluzioni se e solo se il determinante dei coefficienti si annulla. Questa regola è completamente algoritmica e ha costituito una delle prime affermazioni della potenza dei determinanti; Cauchy poté rapidamente dimostrare che essa era in accordo con i metodi precedenti.

Il successivo sostanziale passo in avanti fu il teorema di Noether (1873), un elemento centrale del lavoro da lui svolto con Brill, nell'intento di sviluppare una teoria essenzialmente algebrica delle superfici di Riemann. Il teorema si propone di correggere la seguente affermazione, che a prima vista si potrebbe ritenere vera: date due curve di equazioni f=0 e g=0 e una curva di equazione h=0 passante r+s−1 volte per ogni punto in cui f ha molteplicità r e g ha molteplicità s, esistono polinomi A e B tali che h=Af+Bg. L'affermazione è falsa, come dimostra questo esempio: f(x,y)=y, g(x,y)=y−x2; la curva di equazione x+y=0 non è della forma Af+Bg=0. La correzione di Noether focalizzò l'attenzione sul fatto che i punti singolari hanno la loro importanza. Nell'esempio appena visto è necessaria una formulazione che tenga conto del fatto che la curva h=0 passa per l'origine, ove ha una tangente in comune con le curve f e g. Per esprimersi con il linguaggio del XIX sec., occorre studiare i 'punti infinitamente vicini'. La questione è molto sottile e trascorse molto tempo prima che venissero forniti enunciati precisi e dimostrazioni rigorose (Brill 1892-93, pp. 367-402; Bliss 1923).

Un nuovo livello di profondità in questo ramo dell'algebra fu raggiunto negli anni Ottanta da Leopold Kronecker (Gray 1997). Per tutta la vita Kronecker pensò a come formulare e risolvere i problemi matematici utilizzando l'algebra. La teoria dell'eliminazione era la tecnica fondamentale della sua vasta analisi dei polinomi in più variabili; egli, tra l'altro, considerava anche il caso in cui i coefficienti numerici fossero interi algebrici arbitrari. Il suo lavoro definitivo sull'argomento furono i Grundzüge (1882), pubblicati come parte delle celebrazioni del 50º anniversario del dottorato del suo maestro, Kummer. Si tratta di un lavoro la cui comprensione presenta notevoli difficoltà e può darsi che Kronecker abbia ottenuto maggior successo con le sue lezioni a Berlino e con le relazioni, generalmente buone, che manteneva con i suoi pochi studenti.

L'articolo e le lezioni, pubblicate postume nel 1901, trattano argomenti quali la fattorizzazione dei polinomi (Kronecker affermava di conoscere un metodo generale, che però non ha mai descritto esplicitamente) e la possibilità di sviluppare un polinomio su una data base finita. Egli adottava la terminologia di Gauss per l'aritmetica modulare: se un polinomio f è divisibile per un polinomio g, si dice che f è congruo a 0 mod g. Così, se f si può scrivere nella forma a1g1+…+a_mg_m, dove i coefficienti a_i sono ancora polinomi, Kronecker affermava che f è congruo a 0 mod g1,…,g_m e si riferiva alle funzioni congrue a 0 mod g1,…,g_m come alle funzioni che appartengono al sistema modulare definito dai polinomi g_i. Egli elaborò poi una teoria dei divisori e dei multipli dei sistemi modulari nella quale è incluso anche il concetto di divisore primo.

Le difficoltà insite nella teoria di Kronecker corrispondono strettamente ai problemi geometrici relativi alle curve definite da polinomi, ma Kronecker tendeva a evitare questo linguaggio. Inevitabilmente tali difficoltà crescono al crescere del numero delle variabili. È possibile farsi un'idea di queste difficoltà considerando come i suoi successori hanno cercato di superarle. Jules Molk, studente di Kronecker a Berlino negli anni 1882-1884, pubblicò un lungo articolo sull'argomento negli "Acta Mathematica". Nel 1910, come curatore della Encyclopédie des sciences mathématiques pures et appliqués, Molk organizzò un'ampia rielaborazione dell'articolo di Landsberg sulla teoria dei divisori, che era apparso nella Encyclopädie der mathematischen Wissenschaften; gli autori dell'articolo erano Kürschák e Hadamard. Nel frattempo, il matematico ungherese Gyula König aveva scritto il primo libro di testo sull'argomento (in ungherese nel 1903 e l'anno successivo in tedesco). Tale processo culminò con un articolo e un libro scritti dal matematico inglese F.S. Macaulay.

Molk non fece avanzare la teoria molto oltre il punto in cui l'aveva lasciata Kronecker, osservando che le tecniche disponibili coprivano a stento il caso dei polinomi in due variabili. Il libro di König, anche se mirava a essere semplicemente il primo libro di testo sull'argomento, andò ben oltre. È il primo libro in cui i concetti moderni di 'campo' e di 'anello commutativo' sono chiaramente distinti e utilizzati, anche se i termini introdotti da König non sono sopravvissuti. Egli parlava di 'dominio ortoide' per indicare quello che oggi si chiama campo e di 'dominio oloide' per indicare un anello commutativo con unità, tale che nessuna somma del tipo 1+1+…+1 si annulli (ossia, ciò che oggi è noto come anello di caratteristica zero). Il saggio di Hadamard e Kürschák presenta un interessante elenco di concetti di questo genere, stilato immediatamente prima che l'articolo di Steinitz fondasse la teoria moderna dei campi. König distingue anche tra il concetto di campo e quello di dominio di razionalità. Quest'ultimo è un'estensione finita del campo dei numeri razionali (esistono anche estensioni infinite: König fornisce l'esempio del campo di tutti i numeri algebrici).

L'argomento di maggiore interesse del libro di König è la prima generalizzazione, al caso di n equazioni algebriche in n variabili, di un teorema di Noether relativo alla teoria dell'eliminazione. Questa generalizzazione risponde alla domanda su quando un polinomio in n variabili appartiene al sistema modulare definito da n polinomi dati. Noether aveva sollevato e risolto il problema nel 1873 per due polinomi in due variabili (ossia per due curve) ed era stato il primo ad affrontare in modo corretto le difficoltà relative ai problemi di tangenza. Invece di passare in rassegna le difficoltà affrontate da König, si osservi che il teorema è irrimediabilmente falso per due polinomi in tre variabili.

La teoria dei sistemi modulari non è poi così diversa dalla teoria degli ideali, i cui pionieri sono Dedekind e Weber nel loro articolo del 1882. È più esplicita e algoritmica nei suoi scopi, secondo un approccio che si deve a Kronecker, e fu poi esemplificato da Macaulay. Poiché le pubblicazioni di quest'ultimo su tale argomento si estendono attraverso un arco di tempo che va dal 1913 al 1916, le importanti novità che ha introdotto non possono essere descritte in questa sede; esse rappresentano il percorso attraverso il quale le idee di Kronecker sono penetrate nella moderna 'teoria degli anelli'.

Bibliografia

Bliss 1923: Bliss, Gilbert A., The reduction of singularities of plane curves by birational transformation, "Bulletin of the American mathematical society", 29, 1923, pp. 161-168.

Bottazzini 1981: Bottazzini, Umberto, Il calcolo sublime. Storia dell'analisi matematica da Euler a Weierstrass, Torino, Boringhieri, 1981 (trad. ingl.: The higher calculus. A history of real and complex analysis from Euler to Weierstrass, translated by W. von Egmond, Berlin-New York, Springer, 1986).

Gray 1985: Gray, Jeremy J., Linear differential equations and group theory from Riemann to Poincaré, Basel-Boston, Birkhäuser, 1985.

‒ 1997: Gray, Jeremy J., Algebraic geometry between Noether and Noether. A forgotten chapter in the history of algebraic geometry, "Revue d'histoire des mathématiques", 3, 1997, pp. 1-48.

Hawkins 1974: Hawkins, Thomas W., New light on Frobenius' creation of the theory of group characters, "Archive for history of exact sciences", 12, 1974, pp. 217-243.

‒ 1991: Hawkins, Thomas W., Jacobi and the birth of Lie's theory of groups, "Archive for history of exact sciences", 42, 1991, pp. 187-278.

Lützen 1990: Lützen, Jesper, Joseph Liouville 1809-1882. Master of pure and applied mathematics, New York-Berlin, Springer, 1990.

Montesinos 1987: Montesinos, José M., Classical tessellations and three-manifolds, Berlin-London, Springer, 1987.

Ostrowski 1933: Ostrowski, Alexander M., Über den ersten und vierten Gaussschen Beweis des Fundamentalsatzes der Algebra, Berlin, Springer, 1933.

Purkert 1976: Purkert, Walter, Ein Manuskript Dedekinds über Galois-theorie, "NTM. Schriftenreihe für Geschichte der Naturwissenschaften, Technik und Medizin", 13, 1976, pp. 1-16.

Rider 1982: Rider, Robin E., A bibliography of early modern algebra, 1500-1800, Berkeley, Office for History of Science and Technology, University of California, 1982.

Scholz 1989: Scholz, Erhard, Symmetrie, Gruppe, Dualität, zur Beziehung zwischen theoretischer Mathematik und Anwendungen in Kristallographie und Baustatik des 19. Jahrhunderts, Basel, Birkhäuser, 1989.

Wüssing 1969: Wüssing, Hans, Die Genesis des abstrakten Gruppenbegriffes, ein Beitrag zur Entstehungsgeschichte der abstrakten Gruppentheorie, Berlin, Deutscher Verlag der Wissenschaften, 1969 (ed. ingl.: The genesis of the abstract group concept. A contribution to the history of the origin of abstract group theory, translated by Abe Shenitzer, with the editorial assistance of Hardy Grant, Cambridge (Mass.), MIT Press, 1984).