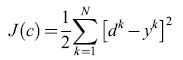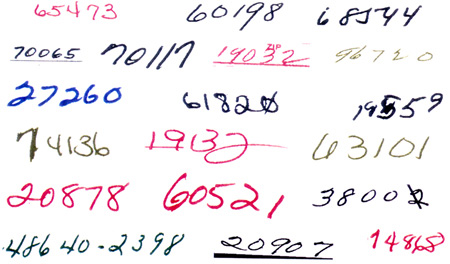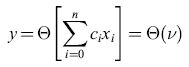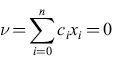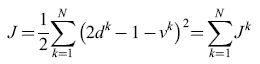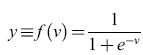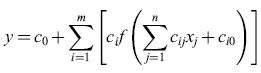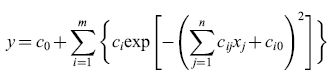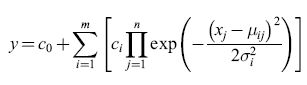Perceptron: passato e presente
Frontiere della Vita (1999)
Perceptron: passato e presente
La storia dei perceptron non è dissimile da quella dell'aeronautica. In tale campo, sebbene l'idea iniziale fosse tratta dall'osservazione del volo degli uccelli, la tecnica del volo ha effettivamente raggiunto lo stadio di piena maturità solo con lo sviluppo approfondito delle conoscenze dell'idrodinamica e della meccanica del volo. Analogamente, negli anni Sessanta, allo scopo di realizzare strutture che imitassero il cervello, furono introdotti i perceptron, le cui applicazioni pratiche tuttavia sono rimaste ancora allo stadio iniziale. In questa rassegna, dapprima illustreremo brevemente lo stato attuale di sviluppo delle reti neurali, sottolineando le loro proprietà matematiche fondamentali e i loro campi di applicazione; successivamente, descriveremo l'evoluzione delle idee in tale campo, dai primi tentativi nel settore del riconoscimento di pattern fino agli sviluppi più recenti nei campi della modellizzazione e del controllo di processi non lineari.
Introduzione
In campo applicativo, lo sviluppo di reti neurali come strutture formali, comprese le strutture denominate perceptron è iniziato negli anni Sessanta. Tuttavia, le ricerche, che a partire circa dagli anni Settanta erano state praticamente abbandonate, sono state riprese solo negli anni Ottanta. Un aspetto saliente degli sviluppi in tale campo consiste nel fatto che, negli ultimi anni, la metafora biologica è risultata quasi del tutto irrilevante, dal punto di vista delle applicazioni in ingegneria, in fisica o in informatica. Infatti, indipendentemente dall'origine biologica delle idee iniziali, i perceptron sono studiati sulla base delle loro intrinseche proprietà matematiche, che li rendono utili in un' ampia gamma di settori. Ovviamente questa osservazione, per quanto utile in ambito applicativo, non deve far dimenticare le idee di base, che sono state tratte dalla biologia, e nemmeno le potenzialità che tali strutture mostrano nello studio di modelli elaborativi in ambito biologico.
Stato attuale delle conoscenze
Neuroni formali e perceptron
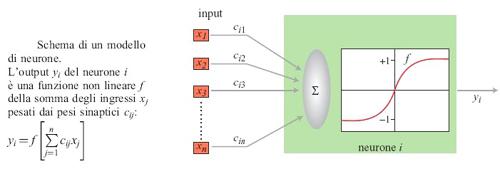
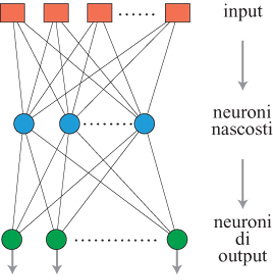
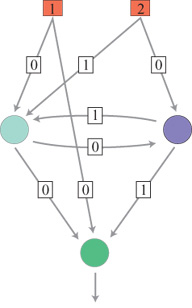
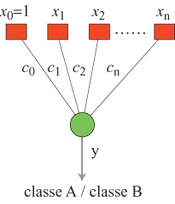
Un neurone formale, che nel prosieguo del saggio sarà chiamato semplicemente neurone, è un semplice operatore matematico che, nella maggioranza delle applicazioni, può essere implementato su calcolatore mediante poche righe di programma. Nei casi in cui siano presenti vincoli sul funzionamento in tempo reale, esso può essere anche realizzato mediante un semplice circuito elettronico. In un neurone sono presenti più grandezze di input che vengono elaborate in modo da ottenere in output una funzione non lineare della somma pesata degli ingressi (fig. 1). Gli ingressi, le uscite e i pesi (detti a volte pesi sinaptici) sono in generale rappresentabili come numeri reali. La funzione non lineare deve essere limitata e può essere, per esempio, una funzione a gradino, una sigmoide (o una tangente iperbolica), una gaussiana e così via. Gli ingressi di un neurone possono essere le uscite di altri neuroni, oppure segnali provenienti dall'esterno. Sebbene la potenzialità di calcolo di un singolo neurone sia molto limitata, reti costituite da molti neuroni possono presentare proprietà assai utili. Prima di descriverle, è opportuno introdurre una distinzione importante tra due classi di architetture neurali: reti neurali feedforward (a propagazione in avanti), nelle quali l'informazione fluisce dagli input agli output, senza alcuna retroazione (fig. 2). Si tratta di sistemi statici, in cui le relazioni input-output sono rappresentabili come equazioni algebriche non lineari e i cui output a un dato istante dipendono solo dagli input allo stesso istante. Nelle reti neurali con retroazione (jeedback), dette anche reti ricorrenti, l'informazione può anche retropropagarsi, dall'uscita di un neurone al suo ingresso, eventualmente attraverso altri neuroni. Si tratta di sistemi dinamici, in cui le relazioni input-output sono rappresentabili come equazioni differenziali non lineari, nel caso di sistemi a tempo continuo, ovvero equazioni alle differenze finite, nel caso di sistemi a tempo discreto (fig. 3). In questo caso, gli output dipendono dai valori assunti in passato dagli input della rete.
Nelle reti feedforward multistrato sono presenti neuroni intermedi, che vengono generalmente detti neuroni 'nascosti', i quali elaborano l'informazione convogliata dagli input e trasmettono i loro risultati ai neuroni di output. Reti di questo tipo sono utilizzate per la classificazione automatica nell'ambito del riconoscimento di pattem, nella realizzazione di modelli non lineari statici di processi. In figura 2 è mostrata una tipica struttura utilizzata per problemi di classificazione, in cui i neuroni nascosti sono organizzati come uno strato intermedio. Sono così presenti connessioni tra gli input e i neuroni nascosti e tra questi ultimi e i neuroni di output.
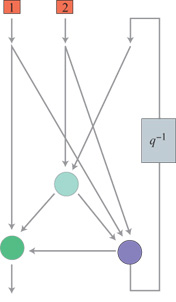
Le reti con retroazione possono essere utilizzate nell'ambito della modellizzazione dinamica non lineare e del controllo di processi. Poiché, in tali reti, si trovano percorsi chiusi in cui fluisce l'informazione, devono essere presenti ritardi affinché il sistema risulti di tipo causale. In effetti, si può mostrare che ogni rete neurale con retroazione, comunque complessa, si può porre in una forma canonica (fig. 4) costituita da una rete feedforward (tipicamente un perceptron multistrato) in cui alcuni output (detti output di stato) sono connessi agli input.
Si noti che, nel corso del tempo, la terminologia in uso nel settore d'interesse ha subito varie evoluzioni. In particolare, mentre in origine il termine perceptron era riservato a una specifica struttura di tipo elementare, in seguito esso è stato esteso fino a includere tutte le reti feedforward.
Proprietà fondamentali dei perceptron multistrato e campi di applicazione
l perceptron multi strato hanno una proprietà notevole: essi sono approssimatori universali (o stimatori di regressione) 'parsimoniosi' (Hornik et al., 1994). La caratteristica di essere un approssimatore universale, per i perceptron, può essere enunciata come segue: ogni funzione non lineare sufficientemente regolare può essere approssimata con accuratezza arbitraria da una rete feedforward, costituita da uno strato contenente un numero fmito di neuroni nascosti, con non linearità di tipo sigmoide, e un singolo neurone di uscita di tipo lineare. Questa proprietà non è specifica delle reti neurali: per esempio, si comportano come approssimatori universali anche i polinomi, le wavelet, le funzioni di base radiali, a così via. Tuttavia, la qualità saliente delle reti neurali, come approssimatori, è il carattere 'parsimonioso': per una data accuratezza, il numero di pesi necessari è generalmente più basso con una rete neurale rispetto ad altri tipi di approssimatori. Per esempio, mentre, nel caso dei perceptron, il numero di pesi cresce in modo lineare con il numero di variabili della funzione, nel caso dei polinomi l'incremento si verifica in modo esponenziale. Nella maggior parte dei casi, tale proprietà rende vantaggioso l'uso dei perceptron, quando il numero delle variabili è maggiore o uguale a tre.
Nella maggior parte delle applicazioni, il compito di un perceptron multi strato non è quello di effettuare l'approssimazione di una funzione nota. Il problema d'interesse può infatti essere enunciato nel modo seguente: assegnati un insieme di valori delle variabili (gli input della rete) e un insieme di numeri (i valori desiderati in output), che sono i corrispondenti valori della funzione non lineare incognita, trovare l'espressione matematica che si adatti nel modo migliore ai dati, cioè che renda minimo l'errore di approssimazione, e che generalizzi nel modo migliore in corrispondenza a nuovi dati, cioè che realizzi la migliore interpolazione. A causa della loro proprietà di essere approssimatori universali e 'parsimoniosi', le reti neurali appaiono come candidati eccellenti a svolgere un tale compito. Il problema consiste quindi nel determinare valori dei pesi che consentano alla rete neurale di realizzare il miglior fit. Questo si ottiene attraverso un particolare algoritmo detto addestramento, o apprendimento supervisionato. Dopo la fase di addestramento, il perceptron dovrebbe idealmente acquisire la capacità di 'cogliere' ciò che, nei dati, è deterministico. Questo è un problema classico, noto, in analisi statistica, come regressione non lineare; l'addestramento infatti non è altro che la stima dei parametri di una regressione non lineare.
Per trovare il miglior fit dei dati fornito dagli output della rete si devono effettuare i seguenti passi: l) scegliere l'architettura della rete, in particolare gli input (cioè le variabili significative), la topologia e le dimensioni della rete; ciò determina una famiglia di funzioni non lineari a parametri incogniti (i pesi della rete) che sono candidate per effettuare in modo corretto il fit desiderato dei dati; 2) effettuare la fase di addestramento della rete, cioè determinare l'insieme di valori dei pesi che minimizzi l'errore di approssimazione sull'insieme di dati usati per l'addestramento (insieme di addestramento); 3) valutare la capacità della rete di generalizzare, cioè valutarne le prestazioni su un nuovo insieme di dati (chiamato insieme di prova, distinto dall'insieme di addestramento, ma originato dalla stessa popolazione).
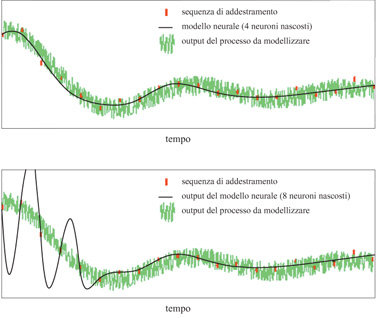
Per la proprietà fondamentale dei perceptron enunciata in precedenza, una rete neurale con un numero sufficientemente grande di neuroni nascosti può adattarsi a qualsiasi funzione non lineare. Tuttavia, se si utilizza una rete con un numero troppo grande di pesi regolabili, essa risulterà eccessivamente flessibile e, oscillando inutilmente sull' insieme dei dati, avrà difficoltà a generalizzare in modo corretto. Al contrario, una rete con un numero troppo piccolo di pesi risulterà troppo rigida e potrà essere incapace ad adattarsi in modo soddisfacente anche ai dati di addestramento. Questo fatto è illustrato in figura (fig. 5): i punti rossi rappresentano le misure degli output del processo, affetti da rumore, che vengono usati per la fase di addestramento della rete, mentre la linea nera rappresenta l'input della rete dopo detta fase. È evidente che l'output della rete con il numero più piccolo di neuroni realizza un'approssimazione della parte deterministica del processo più soddisfacente di quella ottenuta dalla rete più grande.
Pertanto, l'obiettivo principale nel progetto della rete neurale è quello di trovare il miglior compromesso tra l'accuratezza del fit sui dati di addestramento e la capacità della rete di generalizzare, cioè di funzionare in modo corretto su nuovi insiemi di dati. Sono state ampiamente provate sia le tecniche, che a partire da una rete molto piccola, incrementino via via la sua complessità (Nadal, 1989; Knerr et al., 1990), sia quelle che tendono a diminuire la complessità di una rete inizialmente sovradimensionata (Hassibi e Stork, 1993). Esistono metodi statistici rigorosi che forniscono reti quasi ottimali (Leontaritis e Billings, 1987; Urbani et al., 1994). Sono state anche studiate in maniera approfondita tecniche di regolarizzazione, che impongono vincoli ai valori dei pesi (Poggio e Girosi, 1990).
Le aree di applicazione dei perceptron multi strato si possono stabilire facilmente:
l) modellizzazione statica non lineare di processi. Esiste una grande varietà di problemi applicativi, in un'ampia gamma di settori, che sono riconducibili a problemi di fit di dati (v. oltre): per la proprietà dei perceptron di essere approssimatori universali 'parsimoniosi', essi sono eccellenti candidati a svolgere questo compito, purché si disponga di dati adeguati.
2) Modellizzazione dinamica non lineare di processi. Per la loro proprietà di essere approssimatori universali, le reti neurali con retroazione possono essere addestrate a funzionare come modelli per una classe molto ampia di processi dinamici non lineari.
3) Controllo di processi. Un controllore di processo determina i segnali di controllo necessari a conferire al processo una dinamica predeterminata; se il processo è non lineare, si può addestrare una rete neurale a realizzare la funzione non lineare d'interesse.
4) Classificazione. Supponiamo che dei pattern, ciascuno descritto da un insieme di variabili (per es., l'intensità dei pixel di un'immagine), debbano essere classificati in una di due classi, A e B. Un supervisore (di solito un operatore umano) fissa il valore delle uscite a + l per tutti i pattern che riconosce come appartenenti alla classe A, e a O per tutti quelli della classe B. Le reti neurali sono buoni candidati per determinare una funzione che si adatti all'insieme di output desiderati. Si può anche dimostrare che questa funzione fornisce una stima della probabilità che una configurazione non nota appartenga alla classe A. In questo modo, i perceptron danno un'informazione molto ricca, molto più ricca di quella fornita da un semplice classificatore binario. È da notare che la capacità di classificazione delle reti neurali è una conseguenza della proprietà di essere approssimatori universali. Tuttavia, le reti neurali sono state tanto ampiamente studiate e utilizzate in questo contesto, che i perceptron sono per lo più noti come classificatori. Le ragioni storiche di ciò saranno illustrate in seguito.
5) Ottimizzazione. Questo rappresenta l'unico settore di applicazione delle reti neurali che in effetti non si avvantaggia della proprietà di approssimazione universale. Data una rete neurale ricorrente e a tempo discreto, composta di unità binarie (cioè di neuroni la cui funzione di trasferimento non lineare è una funzione a gradino), è di solito possibile definire per questa rete una funzione di Ljapunov (o funzione energia), cioè una funzione scalare dello stato della rete che ha la seguente proprietà: quando la rete viene lasciata evolvere secondo la sua dinamica, la funzione di Ljapunov diminuisce a ogni passo nel tempo, finché la rete raggiunge uno stato stabile. In questo modo, la dinamica della rete conduce a un minimo della funzione di Ljapunov. Si può sfruttare questa proprietà ai fini dell' ottimizzazione nel modo seguente: data una funzione J da ottimizzare, se è possibile progettare una rete neurale la cui funzione di Ljapunov è proprio la funzione J, la rete ha la capacità, se lasciata evolvere liberamente secondo la sua dinamica, di trovare i minimi di questa funzione costo (Hopfield, 1984).
Addestramento supervisionato di reti neurali
Come abbiamo già accennato, la fase di addestramento supervisionato delle reti neurali è il processo attraverso il quale si calcolano i pesi di una rete in modo tale che, per ogni configurazione di input dell'insieme di addestramento, l'output della rete sia, il più possibile, 'vicino' all'output desiderata corrispondente. Quest'ultimo rappresenta la classe a cui la configurazione appartiene (nel caso della classificazione), o l'output misurato del processo da modellare (nel caso della modellizzazione di processi). Si deve quindi definire una 'distanza' Jtra l'uscita della rete (che dipende dai pesi c) e l' output desiderato. Tale distanza (che svolge il ruolo di una funzione costo) di solito viene definita come la somma, su tutti gli esempi k, dei quadrati delle differenze tra gli output effettivi yk e gli output desiderati dk
formula [
dove N è il numero di pattern dell'insieme di addestramento (denominate anche esempi). Se la rete ha più di un output, la somma si estende a tutti gli output. L'addestramento consiste così nella minimizzazione della funzione costo rispetto ai pesi c, che viene effettuata per mezzo dei tipici metodi di ottimizzazione non lineare che fanno uso, in modo iterativo, del gradiente della funzione costo. Il gradi ente viene calcolato attraverso un semplice metodo chiamato retropropagazione (backpropagation; v. il saggio di J. Alspector, Dispositivi neurali elettronici con funzioni specifiche). All'inizio della fase addestramento, si assegnano valori casuali ai pesi. Successivamente, i pesi vengono aggiornati in maniera iterativa, in modo che la funzione J diminuisca, e il processo si considera concluso quando viene raggiunto un compromesso soddisfacente tra l'accuratezza sull'insieme di addestramento e la capacità di generalizzare misurata sull'insieme di test (distinto da quello di addestramento).
Applicazioni delle reti neurali
Modellizzazione statica non lineare di processi
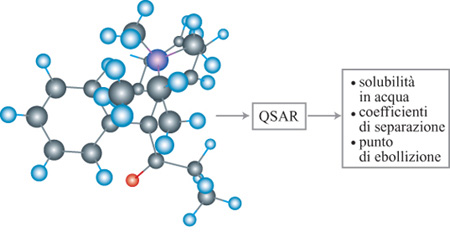
L' applicazione dei perceptron nel settore della Relazione Quantitativa Struttura-Attività (QSAR, Quantitative StructureActivity Relationship) è un tipico esempio della capacità delle reti neurali di realizzare il processo di fit dei dati. Lo scopo è la previsione di una proprietà chimica (espressa da un numero reale) di una molecola a partire da un insieme di descrittori (anch'essi numeri reali) come la massa molecolare, il momento di dipolo, il volume, o altra quantità pertinente (fig. 6). Si possono stimare in questo modo diverse proprietà chimiche, come la solubilità in acqua, i coefficienti di separazione, e così via. Alcuni descrittori si possono misurare, altri si possono calcolare, ab initio, per mezzo di programmi di simulazione molecolare. I risultati ottenuti dalle reti neurali in questo settore sono sistematicamente migliori di quelli ottenuti mediante altre tecniche di regressione sulle stesse basi di dati.
Questo procedimento si può estendere ad altri settori, quali la previsione delle proprietà di materiali compositi a partire dalla loro composizione, la previsione delle proprietà farmacologiche delle molecole, e così via. Si possono quindi considerare i perceptron come un ausilio nella progettazione di nuove molecole o nuovi materiali. Essi possono essere anche molto utili nel far risparmiare il lavoro e i costi necessari a sintetizzare nuove molecole o nuovi materiali, quando, tramite il loro impiego, è possibile prevedere che non possiedono le proprietà desiderate.
Modellizzazione dinamica non lineare di processi
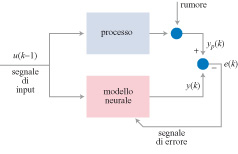
Come già accennato, le reti neurali con retro azione, che obbediscono a equazioni non lineari alle differenze finite, si possono utilizzare per modellare processi dinamici non lineari. Queste applicazioni possono essere considerate come esempi della procedura del tutto generale che realizza una previsione attraverso un'interpolazione. Lo scopo della modellizzazione è trovare un modello matematico, come una rete neurale, la cui risposta a qualsiasi segnale di input (denominato di solito, nel campo del controllo di processi, segnale di controllo) sia identica alla risposta che il processo fornirebbe in assenza di rumore (fig. 7). Molto spesso, si dispone di una conoscenza parziale del processo, nella forma di equazioni differenziali non lineari, dedotte da un'analisi fisica, chimica, economica, finanziaria o di altro tipo, del processo stesso. In tale condizione, sarebbe svantaggioso non far uso di tale informazione utile. Uno degli aspetti più notevoli delle reti neurali è il fatto che esse non sono necessariamente delle 'scatole nere'. Infatti, la conoscenza a priori può essere utilizzata per fornire alla rete una struttura appropriata e determinare i valori di alcuni suoi parametri. Questi modelli neurali basati sulla conoscenza sono effettivamente utilizzati in applicazioni industriali (Ploix e Dreyfus, 1996).
La predizione di una serie temporale a partire dai suoi valori passati è simile alla modellizzazione di un processo, eccetto per il fatto che potrebbero non esserci input di controllo. In tal caso, gli input di un dispositivo neurale di predizione sono costituiti da un insieme appropriato di valori passati tratti dalla stessa serie temporale, ed eventualmente da un insieme di valori passati delle predizioni. In quest'ultimo caso, il dispositivo di predizione è una rete a retroazione. Le previsioni frnanziarie ed economiche sono settori tipici di applicazione della predizione di serie temporali per mezzo di reti neurali (Weigend e Gershenfeld, 1994).
I modelli di un processo possono essere utilizzati in varie applicazioni: rilevazione dei guasti, addestramento del personale, progettazione assistita dal computer, e così via.
Controllo di processi
Il controllo è l'azione attraverso la quale un dato comportamento dinamico viene conferito a un processo. Nei casi in cui è necessario un modello non lineare, le reti neurali sono eccellenti candidati a svolgere tale compito. La progettazione di un controllore neurale di processo si basa su due fattori: un modello di riferimento che calcoli la risposta desiderata del processo in corrispondenza alla sequenza di valori di riferimento; un modello 'neurale', come sopra descritto.
Il controllore neurale viene addestrato a calcolare il segnale di controllo da applicare al modello per ottenere la risposta richiesta dal modello di riferimento.
Per esempio, l'uscita del processo può essere la rotta di un veicolo autonomo, e la variabile di controllo l'angolo di rotazione del suo volante. Allora, se il valore di riferimento è rappresentato dall'angolo desiderato di orientazione del veicolo, il modello di riferimento descrive il modo in cui il veicolo stesso si dovrebbe comportare per effetto di un cambiamento del valore di riferimento, in funzione, per esempio, della velocità del veicolo. Il controllore neurale calcolerà la sequenza di angoli di rotazione del volante necessaria affinché il veicolo raggiunga l' orientazione desiderata con il comportamento dinamico desiderato. È stato progettato e messo in funzione un veicolo a trazione integrale completamente autonomo (fig. 8) nel quale il volante, l'acceleratore e i freni sono controllati da una rete neurale (Rivals et al., 1994).
Problemi di classificazione
In un problema di classificazione, si devono assegnare pattern non noti (intesi in senso generico, per esempio caratteri scritti a mano, serie temporali, fonemi, e così via.) a classi appropriate. I pattern sono rappresentati da una serie di descrittori (numeri reali) che si suppone individuino gli stessi in modo univoco. Un classificatore assegnerà un pattern sconosciuto a una classe, oppure riconoscerà di non poterlo assegnare a nessuna classe, perché esso è ambiguo o troppo diverso dagli esempi. Le prestazioni di un classificatore dipendono fortemente dalla rappresentazione adottata per i pattern che, a sua volta, deriva dai passi di preelaborazione effettuata sui dati grezzi. Nella elaborazione di un'immagine, per esempio, tra le preelaborazioni tipiche figurano il filtraggio, l'estrazione dei contorni, la normalizzazione delle dimensioni, e così via. Se la rappresentazione è discriminante in modo adeguato, se la rete è progettata in maniera appropriata e se l'insieme di addestramento è un campione rappresentativo dei pattern da elaborare, le reti neurali forniscono prestazioni simili a quelle dei migliori classificatori non neurali. Tuttavia, la loro implementazione su circuiti integrati dedicati o su calcolatori paralleli è più semplice che per la maggior parte dei classificatori di qualità equivalente. C'è un'abbondanza di esempi di applicazioni delle reti neurali in questo settore, che sono state studiate in modo approfondito. Le applicazioni industriali hanno avuto molto successo nel campo del riconoscimento di caratteri. Per esempio, in Francia e negli Stati Uniti alcune macchine automatiche per l'ordinamento della posta usano reti neurali (insieme ad altri metodi) per il riconoscimento dei codici postali scritti a mano (fig. 9). Analogamente, si usano reti neurali come componenti di sistemi che leggono automaticamente l'ammontare degli assegni, scritti a mano in corsivo (fig. 10). Anche il riconoscimento della scrittura corsiva a mano in tempo reale è un campo di applicazioni promettente (Guyon e Wang, 1996).
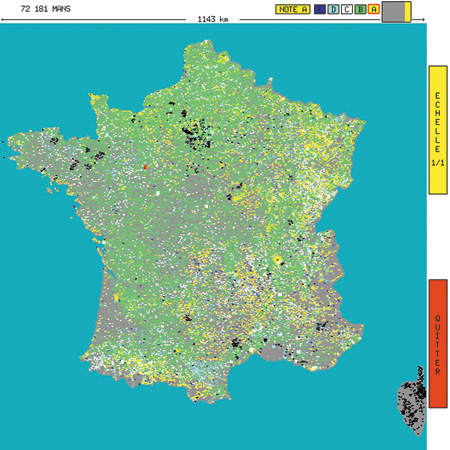
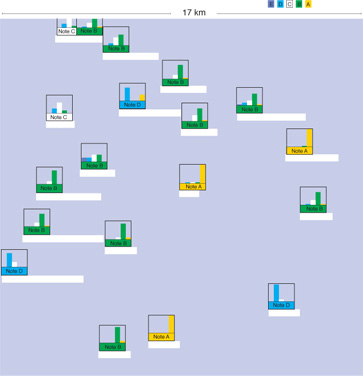
Naturalmente, si presentano dei problemi di classificazione anche in una gamma di applicazioni del tutto diverse dal riconoscimento visivo. I perceptron vengono così utilizzati nell'industria per la diagnosi di guasti, nelle banche per la valutazione delle società, e così via. Per esempio, una banca francese usa una rete neurale per valutare la capacità delle città di restituire i debiti; ogni città è classificata da A (migliore) a E (peggiore). In figura (fig. 11), è mostrata una carta con le città codificate per colore; a ogni città viene assegnato il colore corrispondente alla sua classificazione più probabile.
Passi fondamentali dell'evoluzione della ricerca nel settore
Dopo aver riassunto i principi di base delle reti neurali usate nelle applicazioni mostreremo ora in che modo l'evoluzione della ricerca ha portato allo stato attuale di conoscenza delle loro proprietà matematiche e dei loro settori di applicazione. Storicamente, le prime idee sui neuroni formali (con uscite binarie o continue) sono emerse come astrazioni nel corso degli studi sulle modalità di funzionamento del sistema nervoso (McCulloch e Pitts, 1943), in particolare riguardo la loro capacità di effettuare operazioni logiche e binarie. Negli anni Cinquanta e Sessanta, questi modelli cominciarono a suscitare interesse in campi applicativi, per trovare una risposta alla sfida posta dal riconoscimento automatico e invariante di pattern: come sia possibile che sistemi nervosi molto semplici siano capaci di riconoscere un oggetto, indipendentemente dalla sua dimensione, dalla sua orientazione e dallo sfondo su cui è posto, mentre anche i più potenti calcolatori di oggi sono incapaci di svolgere tale compito. Così, le reti neurali furono all'inizio prese in considerazione per applicazioni nel campo del riconoscimento dei pattern, come lo stesso nome "perceptrom" sta a indicare. L'interesse per le reti neurali riprese nel 1982, con l'introduzione delle reti ricorrenti completamente connesse (note come reti di Hopfield) che sono descritte da equazioni analoghe a quelle che descrivono certi sistemi magnetici, come i vetri di spin (Hopfield, 1982). L'analisi di tali sistemi fu sviluppata nell'ambito della fisica statistica, risolvendo una varietà di modelli dei processi di memorizzazione e apprendimento, e fu esplorato in profondità il loro uso per la modellizzazione di reti biologiche. Poiché le reti neurali sono state utilizzate inizialmente per la classificazione automatica, metteremo qui in evidenza soprattutto il loro ruolo come classificatori, sebbene i legami tra la regressione non lineare (basata sulla proprietà fondamentale delle reti neurali, cioè l'approssimazione di funzioni) e la classificazione non siano del tutto ovvi e siano stati chiariti solo negli ultimi anni. Successivamente descriveremo alcuni sviluppi più recenti.
Classificazione
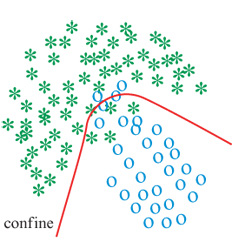
Il problema della classificazione consiste nell'assegnare un pattern, descritto da un insieme di numeri chiamati descrittori, o parametri di regressione, o parametri caratteristici, a una tra diverse classi possibili. Un tipico esempio è il riconoscimento di un numero di codice postale scritto a mano, problema che è divenuto un classico banco di prova per i classificatori. Vi sono due tipi di classificatori, quelli basati sui confini e quelli probabilistici. l primi si basano sui confini tra le regioni che vengono assegnate alle diverse classi nello spazio delle rappresentazioni dei pattern da classificare (fig. 12); questi confini vengono dedotti da un insieme di pattern forniti dal supervisore; quando viene dato in ingresso al classificatore un pattern sconosciuto, il classificatore prende una decisione riguardo alla classe di appartenenza, sulla base della posizione del punto rappresentativo rispetto ai confini. l classificatori probabilistici stimano la probabilità che un pattern appartenga a una certa classe; di nuovo, questa stima è basata su un insieme di pattern la cui classe è nota; quando un pattern sconosciuto viene assegnato in ingresso al classificatore (fig. 13), quest'ultimo stima la probabilità che esso appartenga a ciascuna classe, ma, a differenza del metodo basato sui confini, non prende decisioni circa la classe di appartenenza; la decisione finale viene presa da un ulteriore elemento del sistema sulla base, per esempio, delle informazioni fornite da diversi classificatori che usano differenti rappresentazioni dei pattern.
Il metodo di classificazione neurale basato sui confini. - Supponiamo che sia dato un insieme di pattern, la cui classificazione sia nota, senza errori, a un esperto (o supervisore). Ogni pattern è definito da una rappresentazione dipendente dal problema, cioè da una serie di numeri utili per discriminare le varie classi per l'applicazione d'interesse (per esempio, l'insieme delle intensità dei pixel di un'immagine). Da tale insieme di pattern, si desidera trarre informazioni circa i confini tra le regioni che rappresentano ogni classe nello spazio delle rappresentazioni.
Il più semplice classificatore basato sui confini, per due sole classi, è un neurone binario (o perceptron) singolo, noto anche come separato re lineare (fig. 14). È un neurone la cui non linearità è una funzione a gradino: la sua uscita y è data da
formula [2]
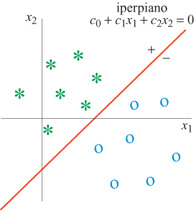
in cui n è il numero di descrittori delle caratteristiche nella rappresentazione scelta, Xo = l, e e è la funzione a gradino di Heaviside. L'uscita del neurone è l se la somma pesata v è positiva, e 0 se è negativa. Il confine è definito nel modo seguente: i pesi ci devono essere tali che l'output del neurone sia uguale a l, se la configurazione considerata appartiene a una delle classi, e sia uguale a 0, se appartiene all'altra classe. Il confine tra le classi è un iperpiano (fig. 15) la cui equazione è
formula. [3]
l pesi ci vengono calcolati applicando un'opportuna procedura di addestramento (v. oltre) al sottoinsieme dei pattern di addestramento (costituito da pattern etichettati con la classe di appartenenza). Se gli esempi dell'insieme di addestramento possono essere separati completamente, senza errori di classificazione, essi vengono detti separabili linearmente.
Sono disponibili diversi algoritmi di addestramento supervisionato per il calcolo dei pesi ci. Il più antico, noto come algoritmo del perceptron, è un metodo iterativo, che usa un insieme di addestramento costituito da pattern etichettati nel modo seguente: un esempio appartenente alla classe A è etichettato con il valore dk = l, un esempio appartenente alla classe B è etichettato con dk = O. Alla k-esima iterazione, il k-esimo esempio viene dato in ingresso al neurone e si calcola la corrispondente somma pesata vk. Se il pattern è classificato correttamente, i pesi vengono lasciati invariati; se invece viene classificato erroneamente, i pesi vengono modificati secondo la procedura del perceptron: ci(k)=ci(k-l)+JL(2dk-l)xβ, dove ci(k) è il valore del peso α all'iterazione k, e il 'tasso di apprendimento' JL è una costante positiva, minore o uguale a l. Tutti gli esempi vengono quindi presentati a turno, in ordine casuale. Si può dimostrare che, se gli esempi di addestramento sono separabili linearmente, questo algoritmo converge a una soluzione valida in un numero finito di iterazioni. Viceversa, se gli esempi non sono separabili linearmente, l' algoritmo non converge e non si arresta, a meno che sia stato specificato un numero massimo di iterazioni.
Nelle applicazioni, il caso di distribuzioni separabili linearmente si presenta di rado. Tuttavia, anche se gli esempi di addestramento non sono separabili linearmente, si può trovare un confine tra le classi minimizzando una funzione costo definita nel modo seguente:
formula [4]
dove N è il numero di esempi. Questo si può ottenere con il noto metodo dei minimi quadrati. Il metodo iterativo di Widrow-Hoff conduce a un unico minimo ben determinato. In ciascuna iterazione, indipendentemente dal fatto che l'esempio presentato sia classificato correttamente o meno, i pesi vengono modificati in direzione opposta al gradi ente, calcolato rispetto ai pesi, di f, termine della funzione costo relativo all'esempio k. In tal modo risulta ci(k)=ci(k-l)+JL(k)(2dk-l-vk)xβ, ove JL(k) è positivo. Si può dimostrare che, poiché J è una funzione quadratica dei pesi, l'algoritmo trova la soluzione (unica) che minimizza J se JL(k) tende a zero. La superficie di confine v = O così ottenuta è una linea retta se la rappresentazione del pattern è bidimensionale (n = 2), un piano se n = 3, e un iperpiano se n> 3. Tale iperpiano, tuttavia, non separa necessariamente i due insiemi di esempi, anche se essi sono separabili linearmente. Nonostante ciò, se le distribuzioni delle classi sono unimodali, la soluzione può essere soddisfacente; se le classi hanno distribuzione gaussiana, la superficie di confine così ottenuta fornisce con certezza l'errore medio di classificazione minimo nell 'uso del classificatore (classificatore di Bayes).
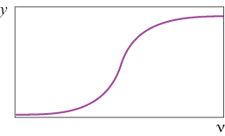
L'algoritmo di Widrow-Hoff, noto in letteratura come regola delta, minimizza una funzione della media pesata v del neurone, ma la quantità che si vorrebbe in effetti minimizzare è la somma delle distanze al quadrato tra l'uscita desiderata dk e l'uscita effettiva yk, data dalla [1] Poiché yk è una funzione non lineare rispetto ai pesi, il metodo dei minimi quadrati non è applicabile. Perciò, per minimizzare J vengono in generale usati metodi basati sul gradiente; questo implica che l'uscita y del neurone sia differenziabile rispetto ai pesi, il che non succede se la non linearità del neurone è una funzione a gradino di Heaviside. Allora la non linearità del neurone non è più Θ(v), ma una funzione sigmoide f(v), che è una versione 'smussata' di una funzione a gradino. Si può scegliere, per esempio,
formula. [5]
La minimizzazione viene effettuata modificando i pesi nella direzione opposta al gradiente rispetto ai pesi del termine della funzione costo relativo all'esempio k:
ci(k) = ci(k- l) + μ(k)(dk - yk)f' (vk) [6]
ove f' è la derivata della funzione sigmoide rispetto a v. Questa regola è nota come regola delta generalizzata. Una volta che il neurone è stato addestrato, la presentazione di un pattern al suo ingresso produce una risposta che, al contrario del caso precedente, non è binaria, ma può assumere valori continui tra 0 e 1 (fig. 16). Perciò il neurone non prende una decisione riguardo alla classe di appartenenza del pattern. Spetta invece all'utilizzatore stabilire un meccanismo di decisione, il più semplice dei quali consiste nell'assegnare il pattern alla classe A se y > 0, 5 e alla classe B se y<0,5. Con tale scelta, l'iperpiano definito da (o v(x) = 0) diventa il confine tra le classi.
Tutti i metodi descritti, nei quali i pesi sono calcolati a partire dagli esempi, conducono a una domanda essenziale: quanti esempi sono necessari per ottenere un confine significativo? Questa è una domanda difficile, che non ha ancora ricevuto una risposta completa e generale. Un interessante elemento di comprensione del problema viene dal risultato seguente (Cover, 1965). Consideriamo un insieme di N punti distribuiti a caso in uno spazio n-dimensionale e si realizzi a caso una dicotomia in questo insieme (si assegni cioè a caso ogni punto a una delle due classi con probabilità 0,5). T.M. Cover ha dimostrato che:
l) se il numero N di esempi è minore del numero n di descrittori (N<n), qualsiasi dicotomia dell'insieme di esempi fornisce due sotto insiemi che sono separabili linearmente.
2) Se la dimensionalità dello spazio delle rappresentazioni è grande (per esempio n > 100) e se il numero di esempi è minore o uguale al doppio del numero di descrittori (N≤2n), allora quasi ogni dicotomia fornisce due sotto insiemi che sono separabili linearmente. Pertanto, se il numero di esempi non è molto grande rispetto al numero di descrittori, può esistere un confine lineare tra le due classi, ma questo può essere completamente privo di significato, portando quindi a una cattiva classificazione dei pattem che non sono nell'insieme di addestramento. Quantitativamente, si può dimostrare che il numero di esempi necessario per una separazione significativa tra le classi cresce esponenzialmente con n. Quindi sono altamente desiderabili rappresentazioni compatte che usino un piccolo numero di descrittori; questo fatto viene a volte chiamato 'flagello della dimensionalità.
È interessante il fatto che le tecniche sopra menzionate per addestrare neuroni singoli siano state applicate alle reti di Hopfield. Poiché tutti i neuroni di queste reti sono connessi tra loro, essi hanno tutti ingressi simili; di conseguenza, risulta che il comportamento dei perceptron a un solo strato sia molto rilevante ai fini della comprensione del comportamento dinamico globale di queste reti in presenza di retroazione.
Si può ora passare dal neurone singolo alle reti di neuroni. Poiché il singolo neurone è un separatore lineare, se gli esempi non sono linearmente separabili, come si può procedere? Una rete di neuroni feedforward multi strato è in grado di determinare superfici di confine di forma arbitraria. La ragione di questo fatto si comprende meglio nel contesto dell' approccio probabilistico alla classificazione.
L'approccio probabilistico alla classificazione neurale
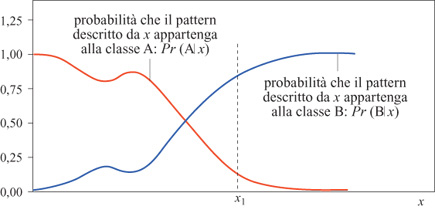
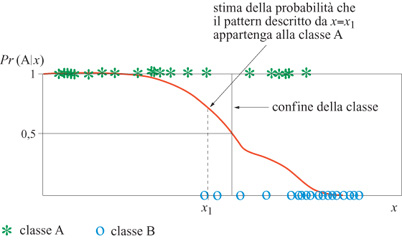
Come abbiamo già detto, il legame tra le proprietà di classificazione delle reti neurali e la loro proprietà di approssimazione è il seguente: quando si usa la regola delta generalizzata, l'uscita desiderata del neurone è l se l'esempio appartiene alla classe A, o 0 se l'esempio appartiene alla classe B. La stessa idea può essere usata per addestrare una rete neurale feedforward. È infatti noto che, per la proprietà fondamentale delle reti neurali, la rete, dopo l' addestramento, fornisce un'approssimazione della probabilità, Pr(Alx), che un pattern descritto da un vettore x appartenga alla classe A. Questo si ottiene minimizzando la [l] in cui dk = l se il pattern appartiene ad A, dk = O se non appartiene ad A, e yk è l'uscita della rete. Se gli esempi sono ben scelti e abbastanza numerosi, se il numero di neuroni nascosti è appropriato e se l'algoritmo di addestramento è efficiente, questa approssimazione è molto buona. Questo viene illustrato dalla figura (fig. 17) nel caso di una rappresentazione monodimensionale.
Una volta che sia stata stimata la probabilità, si deve scegliere una regola per il calcolo dei confrni della classe; la scelta più naturale, che minimizza il rischio di errore, è di scegliere la superficie che corrisponde a uguali probabilità di appartenere a ognuna delle classi: Pr(Alx) =Pr(Blx) = 0, 5. Questa relazione defrnisce una ipersuperficie nello spazio delle rappresentazioni. Siccome la rete feedforward può approssimare qualsiasi funzione, la ipersuperficie così definita può avere una forma arbitraria. Quindi, una rete neurale feedforward con un neurone di uscita può definire superfici di confine arbitrarie tra due classi. Si può estendere lo stesso principio alla determinazione delle superfici di confine tra diverse classi. Per un problema con C classi, si usa generalmente una rete neurale con C uscite. Durante l'addestramento, il valore desiderato per l'uscita c è l se l'esempio appartiene alla classe c, e 0 altrimenti. La rete usa così un codice del tipo' l tra C' per le classi. Per poter interpretare le uscite come probabilità, la loro somma deve essere vincolata ad avere un valore uguale a l (Bridle, 1990). Le considerazioni fatte permettono di spiegare perché le reti neurali siano capaci di calcolare superfici di confine di forma arbitraria. Si deve tuttavia sottolineare che nella classificazione probabilistica c'è molto di più della semplice determinazione dei confini delle superfici. Si usa, nelle applicazioni reali, avere diversi classificatori che prendono decisioni a partire da varie sorgenti di informazione (per esempio, si possono usare diverse rappresentazioni dei pattern e avere così diversi classificatori che usano queste rappresentazioni). Quindi, la decisione finale viene presa in base ai punteggi ottenuti dai classificatori. Tipicamente, in un'applicazione di riconoscimento di caratteri, ogni classificatore fornisce una lista di ipotesi riguardo il carattere da determinare, ordinate in ordine decrescente di probabilità. In applicazioni di tipo bancario, e più in generale nelle applicazioni di presa di decisioni assistita dal calcolatore, può essere utile assegnare una valutazione graduata. Nell'applicazione sopra menzionata delle reti neurali alla valutazione delle capacità frnanziarie delle città, un risultato tipico risulta della forma: questa città ha il 78% di probabilità di appartenere alla classe B, il 19% di probabilità di appartenere alla classe C, e l'1% di essere in A, D ed E. Questo è illustrato nella figura (fig. 18), che mostra un ingrandimento di una particolare zona della Francia, in cui un grafico a barre indica le probabilità stimate per ogni città di appartenere a ognuna delle classi.
Modellizzazione di processi dinamici
Un processo, sia esso fisico, chimico, biologico, economico, ecologico, o di alto tipo, si può modellizzare utilizzando due diverse sorgenti di informazione: la conoscenza del processo, espressa matematicamente da equazioni differenziali che collegano le variabili interessanti (fisiche, chimiche, e così via) e le misure effettuate sul processo. Come già accennato, i modelli che sfruttano essenzialmente la conoscenza del processo sono detti modelli basati sulla conoscenza. Questi hanno, di solito, un piccolo numero di parametri, che vengono determinati da misure effettuate sul processo. l modelli che sfruttano prevalentemente le misure effettuate sul processo sono definiti modelli a scatola nera. l modelli basati sulla conoscenza vengono preferiti di solito a quelli a scatola nera poiché risultano più intellegibili, dato che le equazioni matematiche e le variabili hanno un significato ben definito. Tuttavia, nelle applicazioni, è molto spesso disponibile un'informazione a priori scarsa o non utilizzabile, cosicché un modello deve essere dedotto essenzialmente dalle sole misure. Inoltre, i modelli a scatola nera vengono utilizzati frequentemente, anche ove esistano modelli basati sulla conoscenza, nel caso in cui le equazioni di questi ultimi non si possano risolvere con le risorse di calcolo disponibili.
Un modello a scatola nera è definito in primo luogo dai suoi input, che sono le variabili che agiscono sul processo, e dai suoi output. Occorre distinguere due tipi di input: quelli di controllo, sui quali si può agire deliberatamente per controllare il processo, e i disturbi, che agiscono sul processo in modo non controllabile, o perfino non misurabile. Per esempio, la corrente elettrica in una resistenza è un ingresso di controllo in un forno nel quale vogliamo mantenere la temperatura a un certo valore, mentre le temperature non note degli oggetti che vengono messi nel forno, in istanti impredicibili, sono le grandezze di disturbo. Gli output del processo sono le variabili interessanti che vengono misurate: nell'esempio precedente, la temperatura del forno è la grandezza di output del processo. Anche le grandezze di output possono essere soggette a disturbi, in particolare quelli derivanti dal rumore dei sensori.
Un modello a scatola nera si utilizza per fornire le relazioni matematiche tra le grandezze misurabili di input e quelle di output. Tali relazioni coinvolgono parametri incogniti, che debbono essere stimati in base alle misure fatte sugli input e sugli output. Poiché queste misure sono influenzate da disturbi e rumore, il modello dovrebbe identificare la parte predicibile delle variazioni delle variabili di output sotto l'effetto delle variabili di input; in altre parole, la previsione fatta dal modello dovrebbe essere uguale all'uscita che si sarebbe misurata sul processo se non fossero stati presenti disturbi. Se l'effetto di questi può essere modellizzato in modo appropriato come un rumore bianco additivo, la varianza dell'errore delle previsioni del modello dovrebbe uguagliare quella del disturbo.
l modelli a scatola nera di sistemi dinamici lineari sono stati studiati a fondo per molti anni. Se ipotizziamo che esista una funzione non lineare incognita che descrive il comportamento del processo, le reti neurali sono candidate ideali per la modellizzazione di sistemi dinamici non lineari, visto che possono approssimare qualsiasi funzione non lineare. In effetti, molti concetti che compaiono nella modellizzazione non lineare sono estensioni di idee sviluppate nell'ambito della modellizzazione di sistemi lineari (Narendra et al., 1990).
Nella prima parte di questo saggio, si è detto che ogni rete neurale dinamica si può porre in una forma canonica, costituita da una rete feedforward con gli output di stato retropropagati agli input (Nerrand et al., 1993). Pertanto, è opportuno considerare in primo luogo le reti feedforward, come modelli stati ci. In un modello lineare (affine) statico l'output ha la forma generale:
y=bo+b)x) +b2X2+ ... +bnxn, [7]
dove le Xi sono le variabili di input. Una prima naturale estensione non lineare del modello è la seguente:
y = Co + c1 Φ1 (x1), ... ,xn)+
+C2Φ2 (x1, ... ,xn) + ... + cmΦm(x1, ... ,xn)
dove le Φi sono funzioni non lineari delle variabili scelte in modo opportuno. In questo modo, y risulta non lineare rispetto agli ingressi, ma lineare rispetto ai coefficienti ci. Questi ultimi si possono quindi stimare con il normale metodo dei minimi quadrati dai valori misurati delle uscite del processo yp e delle funzioni Φ1, Φ2,..., Φm.
Nei metodi convenzionali in uso in ingegneria, le funzioni non lineari Φi sono monomi, cosicché il modello risulta polinomiale. Il vantaggio principale di tale modello è il fatto che l'uscita è lineare rispetto ai pesi, in modo da poter usare il metodo dei minimi quadrati; l'inconveniente principale è rappresentato dal fatto che i modelli polinomiali con diversi ingressi e grado elevato tendono ad avere un numero molto grande di monomi, e quindi un numero molto grande di coefficienti. L'assenza del carattere 'parsimonioso' rende obbligatorio l'uso di metodi di selezione degli input. Al contrario, le reti neurali possono fornire un modello 'parsimonioso' di un processo nella regione dello spazio degli input in cui si sono fatte le misure usate per addestrare la rete. L'uscita di una semplice rete feedforward con n ingressi, m neuroni nascosti con funzione di attivazione f e un neurone di uscita lineare, sarà tipicamente della forma
formula. [8]
Pertanto l'uscita non è più lineare rispetto ai pesi, cosicché il normale metodo dei minimi quadrati non è più applicabile, come già affermato. Occorre allora far ricorso a metodi di ottimizzazione non lineare, usando l'algoritmo di backpropagation per calcolare il gradiente della funzione costo.
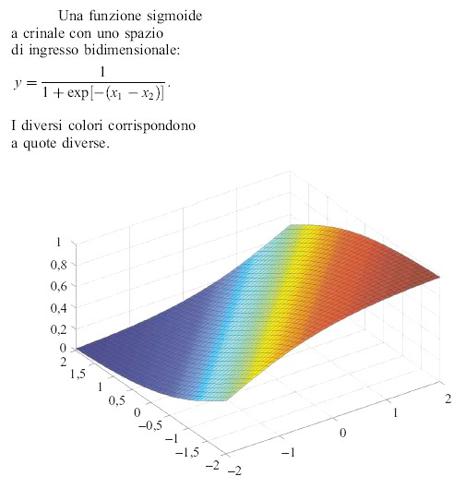
Il fatto che la funzione di attivazione non lineare f sia molto spesso una sigmoide deriva da diversi fattori. Storicamente, le sigmoidi all'inizio sono state usate nella classificazione, come varianti 'regolari' della funzione gradino; inoltre risulta che, per l'approssimazione di funzioni, le sigmoidi sono molto semplici da utilizzare, specialmente durante l'addestramento. Occorre tuttavia notare che le reti di sigmoidi non sono sempre la migliore soluzione per un dato problema; tale soluzione dipende, in effetti, dall'insieme di addestramento (numero e distribuzione degli esempi usati per l'addestramento), dall' architettura della rete (la funzione incognita, o una sua approssimazione accettabile, deve far parte della famiglia di funzioni generate dalla rete), dall'algoritmo di addestramento, e dalla procedura utilizzata di selezione del modello. Le reti neurali con attivazione sigmoide sono membri della famiglia generale di reti con funzioni 'a crinale' che dipendono dalla somma pesata degli ingressi (fig. 19).
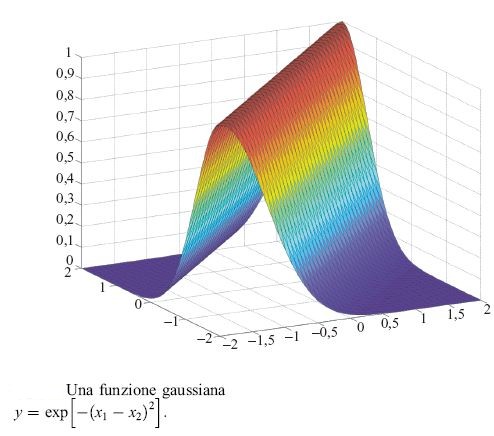
Si possono usare funzioni gaussiane invece che funzioni a crinale sigmoidi (fig. 20):
formula [9]
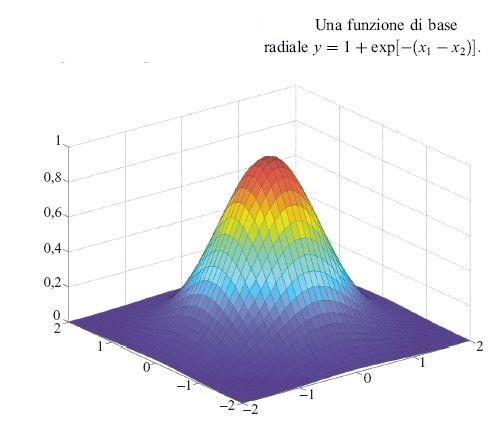
Sono state studiate anche funzioni a crinale di tipo wavelet (Benveniste et al., 1996). Sono state considerate anche funzioni non a crinale (fig. 21), come le funzioni di base radiali (Moody e Danken, 1989):
formula [10]
dove μij è la j-esima coordinata del centro della gaussiana i con larghezza σi. Sono stati seguiti due approcci: scegliere a priori il numero, i centri e le larghezze delle gaussiane, e stimare soltanto i pesi ci (si noti che l'uscita è lineare rispetto ai pesi, cosicché si può usare il metodo dei minimi quadrati), o scegliere solo il numero delle gaussiane e stimare i pesi, le posizioni dei centri e le larghezze (il che richiede una minimizzazione non lineare).
Si noti che in tutti i casi in cui viene richiesta una ottimizzazione non lineare, i metodi basati sul gradi ente del secondo ordine risultano migliori rispetto ai metodi basati sul gradi ente semplici, già menzionati per i neuroni singoli. La descrizione dei metodi di minimizzazione del secondo ordine va oltre l'obiettivo di questo breve saggio; si rimanda a testi standard sulla ottimizzazione non lineare o sulla analisi numerica (Press et al., 1992).
Avendo discusso le varie forme di reti feedforward, le consideriamo adesso come parte della forma canonica di una rete ricorrente usata come modello dinamico. In un modello di questo tipo, gli input e gli output sono funzioni del tempo. Limitandoci a considerare modelli del tipo a tempo discreto, il loro comportamento è descritto da sequenze di valori campionati in istanti discreti di tempo. Tali modelli (modelli input-output) sono quindi descritti da equazioni alle differenze finite del tipo
y(k) = ϕ[y(k-l), ... ,y(k-n),u(k-l), ... ,u(k-m)], [11]
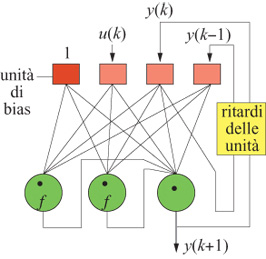
in cui y è l'output del modello e u è l'input di controllo. In questo modo, la funzione q;, che determina l'output al tempo k a partire dagli output e dagli input a istanti precedenti, definisce completamente la dinamica del modello. Tale funzione può essere realizzata per mezzo di una rete neurale feedforward di uno qualunque dei tipi summenzionati. Tuttavia, i modelli ingresso-uscita non sono la forma più generale di modelli dinamici. È stato dimostrato che la forma del tipo spazio degli stati,
x(k) = ϕ[x(k-l),u(k-l)] [12]
y(k) = ψ[x(k)], [13]
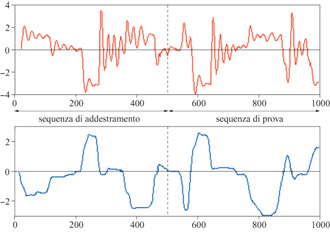
dove le x(k) sono le variabili di stato con componenti, è in genere più 'parsimoniosa' della forma input-output (Levin e Nerendra, 1995). Per illustrare le capacità di modellizzazione non lineare delle reti neurali, e la differenza tra i modelli di tipo inputoutput e quelli di tipo spazio degli stati, consideriamo la modellizzazione dell'attuatore idraulico del braccio di un robot. Si tratta di un processo con un input (l'angolo di apertura della valvola del circuito idraulico) e un output (la pressione del circuito idraulico). In figura (fig. 22) sono mostrate le sequenze di addestramento e di prova.
Utilizzando un modello input-output, i risultati migliori sono stati ottenuti con la rete del secondo ordine mostrata in figura (fig. 23), con due neuroni nascosti (e con funzione di attivazione sigmoide).
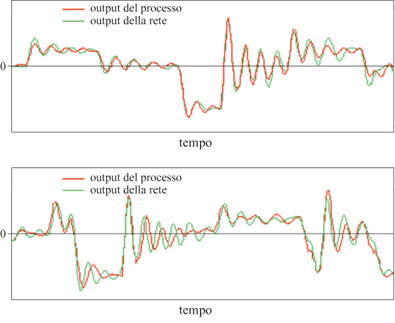
In figura (fig. 24), è mostrato il risultato ottenuto dopo l'addestramento. L'errore quadratico medio di previsione sulla sequenza di addestramento è uguale a 0,085, mentre l'errore di previsione sulla sequenza di test è 0,30. Questo è un chiaro indizio del verificarsi del fenomeno di overfitting (sovrainterpolazione), a causa del numero relativamente basso di esempI.
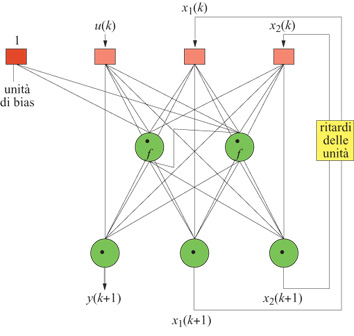
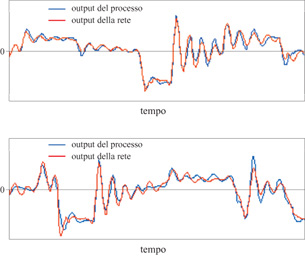
Con il modello a spazio degli stati (fig. 25), i risultati sull'insieme di test sono quelli mostrati nella figura (fig. 26). L'errore quadratico medio è 0,10 sulla sequenza di addestramento e 0,11 sulla sequenza di test, risultato migliore rispetto a quelli ottenuti con il modello input-output. Questo fatto illustra chiaramente il vantaggio nell'uso di dispositivi di previsione a spazio degli stati, nei casi in cui sono disponibili solo insiemi di addestramento piccoli. Poiché richiedono un numero minore di ingressi, questi modelli sono più 'parsimoniosi' e quindi meno esposti al fenomeno di overfitting.
Conclusioni
La scienza delle reti neurali è un campo aperto e affascinante, all'incrocio tra la biologia, la fisica e l'ingegneria. A conclusione di questo breve saggio dedicato principalmente alle prospettive di utilizzo delle reti neurali formali in applicazioni pratiche, è opportuno dire qualcosa in un contesto più ampio.
In senso stretto, come pure in architetture feedforward, i perceptron rappresentano gli elementi di base di tutti gli studi di reti neurali basati sulla fisica statistica. In questi approcci si considera il limite in cui il numero di ingressi è infinito (simile al limite di numero infrnito di particelle in termodinamica); questa apparente complicazione risulta molto fertile, perché consente la soluzione di molti modelli importanti per la memorizzazione, l'apprendimento di regole (Watkin et al., 1993), la generalizzazione, e così via. Inoltre, i risultati esatti dedotti da queste strutture di tipo perceptron servono come fondamento per lo studio di reti più generali, che includono connessioni con retroazione. In effetti, la presenza di connessioni bidirezionali (con retroazione) è una caratteristica generale dei sistemi nervosi biologici. Nonostante questo fatto anatomico notevole, la modellizzazione neurobiologica basata su reti feedforward è un attivo settore di ricerca, e si possono citare almeno quattro buoni motivi: questi modelli forniscono spesso un'approssimazione del primo ordine su cui si può lavorare; possono servire come passi intermedi verso miglioramenti di ordine superiore; in alcune funzioni fisiologiche, l'elaborazione neuronale è in effetti così veloce e direzionale (si pensi per esempio l'arco riflesso) che l'elaborazione feedforward ne contiene l'essenza; infine, c'è la possibilità per il futuro di trarre fonte di ispirazione dalle analogie con le proprietà computazionali e algoritmiche delle reti formali, sviluppate per applicazioni di interesse pratico.
Bibliografia citata
BENVENISTE, A., JUDITSKY, A., DELYON, B., ZHANG, Q., GLORENNEC, P.-Y. (1994) 10th IFAC Symposium on Identification, Copenhagen.
BRIDLE, J.S. (1990) In Neurocomputing: Algorithms, Architectures and Applications, Proceedings of the NATO Advanced Research Workshop on Neuro-computing, a c. di Fogelman-Soulie F., Herault J., Berlino-New York, Springer Verlag, pp. 227-236.
COVER, T.M. (1965) IEEE Transactions on Electronic Computers 14, 326-334.
GUYON, I., WANG, P.S.P. (1994) Advances in pattern recognition systems using neural network technologies. Singapore-River Edge, World Scientific.
HASSIBI, B., STORK, D.G. (1993) Advances in Neural Information Processing Systems, 5, 164-171.
HOPFIELD, U. (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. NatI. Acad. Sci. USA, 79, 2554-2558.
HOPFIELD, J.J. (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA, 81, 3088-3092.
HORNIK, K., STINCHCOMBE, M., WHITE, H., AUER, P. (1994) Neural Computation, 6, 1262-1275.
KNERR, S., PERSONNAZ, L., DREYFUS, G. (1990). In Neurocomputing: Algorithms, Architectures and Applications, Proceedings of the NATO Advanced Research Workshop on Neuro-computing, a c. di Fogelman-Soulie F., Herault J., Berlino-New York, Springer Verlag, pp. 41-50.
LEONTARITIS, I.J., BILLINGS, S.A. (1987) Int. J. Control, 1, 311-341.
LEVIN, A.D., NARENDRA, K.S. (1995) Neural Computation, 7, 349-357.
McCULLOCH, W.S., PITTS, W.H. (1943) Bull. Math. Bioph., 3, 115-133.
MOODY, J.E., DARKEN, C.J. (1989) Neural Computation, l, 281-294.
NADAL, J.P. (1989) International Journal of Neural Systems, 1,55-59.
NARENDRA K.S., PARTHASARATHY K. (1990) IEEE Trans. on Neural Networks, 1, 4-27.
NERRAND, O., ROUSSEL-RAGOT, P., PERSONNAZ, L., DREYFUS, G. (1993) Neural Computation, 5, 165-199.
PLOIX, J.L., DREYFUS, G. (1996). In IndustriaI applications of neural networks, a c. di Fogelman-Soulie F., Gallinari P., Singapore-River Edge, World Scientific.
POGGIO, T., GIROSI, F. (1990) Science, 247, 1481-1497.
PRESS, W.H., TEUKOLSKY, S.A., VETTERLING, W.T., FLANNERY, B.P. (1992) Numerical recipes in C: the art of scientific computing, 2a ed., Cambridge-New York, Cambridge University Press.
RIVALS, I., CANAS, D., PERSONNAZ, L., DREYFUS, G. (1994) Proceedings of the IEEE Conference on Intelligent Vehicles, 137-142.
URBANI, D., ROUSSEL-RAGOT, P., PERSONNAZ, L., DREYFUS, G. (1994) Neural Networks for Signal Processing, 4, 229-237.
WATKIN, T.L.H., RAU, M., BIEHL, M. (1993) Rev. Mod. Phys., 65, 499-556.
WEIGEND, A.S., GERSHENFELD, N.A, a c. di (1994) Time series prediction: forecasting the future and understanding the past: Proceedings of the NATO Advanced Research Workshop on Comparative Time Series Analysis, Reading, Addison-Wesley Pubbl. Co.
Bibliografia generale
ARBIB, M., a c. di, Handbook ofbrain theory and neural networks, Cambridge, Mass., MIT Press., 1995.
BISHOP, C.M. Neural networks for pattern recognition, Oxford, Clarendon Press and Oxford-New York, Oxford University Press, 1995.
DUDA, R.O., HART, P.E. Pattern classification and scene analysis, New York, Wiley, 1973.
GRASSBERGER, P., NADAL, J.P., a c. di, From Statistical Physics to Statistical Inference and back. Proceedings of the NATO Advanced Study Institute, Dordrecht-Boston, Kluwer Academic. 1994.
GUTFREUND, H., TOULOUSE, G., a c. di, Biology and computation: a physicist's choice, Singapore-River Edge, World Scientific, 1994.
HERTZ, J., KROGH, A., PALMER, R.G. Introduction to the theory of neural computation, Redford City, Addison-Wesley, 1991.
LJUNG, L. System identification; theory for the user, Englewood Cliffs, Prentice Hall, 1987.
MINSKY, M., PAPERT, S. Perceptrons: an introduction to computational geometry, Cambridge, Mass., MIT Press, 1969.
RUMELHART, D.E., HINTON, G.E., WILLIAMS, R.J. Parallel distributed processing: explorations into the microstructure of cognition, Cambridge, Mass., MIT Press, 1986.
STEIN, D., Spin glasses and biology. Singapore-River Edge, World Scientific, 1992
© Istituto della Enciclopedia Italiana - Riproduzione riservata